Wortel betekent vierkant

Hier leggen we uit wat het root mean square is en hoe het wordt berekend. Daarnaast leer je de voor- en nadelen van het gebruik van het gemiddelde en een stap-voor-stap opgeloste oefening. Ten slotte kunt u met de rekenmachine aan het einde van dit artikel het wortelgemiddelde van elke dataset berekenen.

Wat is het gemiddelde vierkant?

Het wortelgemiddelde kwadraat is een maatstaf voor de centrale plaats van beschrijvende statistieken. Het wortelgemiddelde kwadraat is gelijk aan de vierkantswortel van het rekenkundig gemiddelde van de kwadraten van de gegevens.

Root mean square wordt ook wel root mean square of RMS genoemd.

De formule voor het kwadratisch gemiddelde is daarom als volgt:

Het kwadraatgemiddelde is vooral handig wanneer de statistische variabele positieve en negatieve waarden aanneemt, omdat door elk stukje gegevens te kwadrateren alle waarden positief worden. Daarom wordt het gemiddelde kwadraat gebruikt om variabelen te analyseren waarin het teken niet belangrijk is, maar de absolute waarde ervan.

Het gemiddelde kwadraat wordt bijvoorbeeld gebruikt om meetfouten te bestuderen, omdat we in deze gevallen niet kijken of de fout positief of negatief is, maar eerder de omvang van de fout analyseren bij het meten.

Bovendien hebben de vierkanten van grote getallen veel hogere waarden dan de vierkanten van kleine getallen, dus in het middelste vierkant zijn grote getallen belangrijker dan kleine getallen.

Het kwadraatgemiddelde is een soort statistisch gemiddelde, samen met het rekenkundig gemiddelde, het gewogen gemiddelde, het geometrische gemiddelde en het harmonische gemiddelde.

Voor- en nadelen van Root Mean Square

Het kwadratische gemiddelde heeft voor- en nadelen vergeleken met andere soorten gemiddelden.

Het belangrijkste voordeel van het kwadratisch gemiddelde is dat u hiermee een zeer goede benadering van de gemiddelde waarde van een discrete variabele kunt verkrijgen. Aan de andere kant is het grote nadeel van het kwadraatgemiddelde dat de berekening ervan behoorlijk ingewikkeld is, omdat er meerdere bewerkingen moeten worden uitgevoerd.

Het root mean square is daarentegen erg handig voor het analyseren van foutmetingen. Er wordt ook veel meer belang gehecht aan hoge waarden, hoewel deze eigenschap impliceert dat een verkeerde meting het effectieve resultaat aanzienlijk zal veranderen.

Hoe het wortelgemiddelde kwadraat te berekenen

Om het wortelgemiddelde kwadraat te berekenen, moeten de volgende stappen worden uitgevoerd:

1. Bereken het kwadraat van elke statistische gegevens.
2. Tel alle vierkanten op die in de vorige stap zijn berekend.
3. Deel het resultaat door het aantal gegevensitems in de steekproef.
4. Zoek de vierkantswortel van de vorige waarde.
5. Het verkregen resultaat is het kwadraatgemiddelde van de statistische steekproef.

👉 U kunt de onderstaande rekenmachine gebruiken om het wortelgemiddelde van elke dataset te berekenen.

Bedoel vierkant voorbeeld

Zodra we weten hoe we het wortelgemiddelde van het kwadraat kunnen bepalen, bepalen we als voorbeeld het wortelgemiddelde van een reeks gegevens.

• In een universitair laboratoriumklas vraagt de professor zijn studenten om een experiment met chemicaliën te doen. Het doel van het chemische experiment is om een oplossing van in totaal 3 liter te verkrijgen. De studentengroepen verkregen de volgende gegevens:

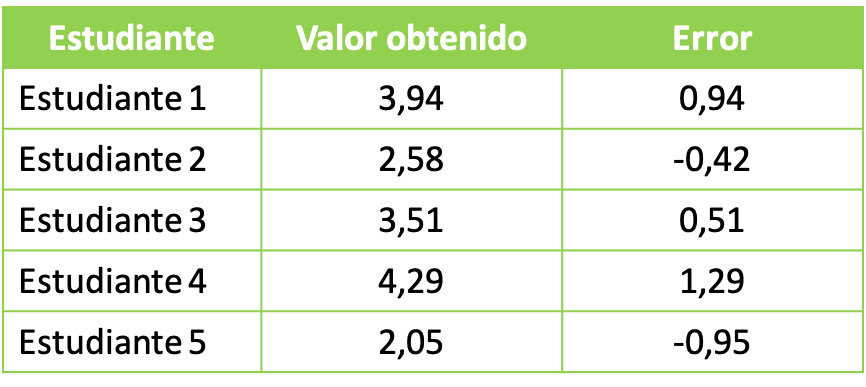
Om de verkregen statistische gegevens te bestuderen, gaan we verder met het berekenen van de waarde van het kwadraatgemiddelde met de door elke groep verkregen fout. We passen daarom de formule voor het kwadratisch gemiddelde toe:

En we vervangen de gegevens in de formule en berekenen het wortelgemiddelde kwadraat:

De gemiddelde fout die in het experiment wordt verkregen, volgens het wortelgemiddelde, bedraagt dus 0,88 liter.

Gemiddelde vierkante rekenmachine

Voer gegevens uit een statistisch monster in de volgende rekenmachine in om het wortelgemiddelde kwadraat ervan te berekenen. Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.