Fisher's minst significante verschil: definitie + voorbeeld
Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.
De aannames die bij een ANOVA worden gebruikt, zijn als volgt:
H 0 : De gemiddelden zijn voor elke groep gelijk.
H A : Minstens één van de manieren is anders dan de andere.
Als de p-waarde van de ANOVA onder een bepaald significantieniveau ligt (zoals α = 0,05), kunnen we de nulhypothese verwerpen en concluderen dat ten minste één van de groepsgemiddelden verschilt van de andere.
Maar om precies te weten welke groepen van elkaar verschillen, moeten we een post-hoc test doen.
Een veelgebruikte post-hoc-test is de minst significante verschiltest van Fisher .
Om deze test uit te voeren, berekenen we eerst de volgende teststatistiek:
LSD = t 0,025 , DF w * √ MS W (1/n 1 + 1/n 1 )
Goud:
- t .025 , DFw : De t-kritische waarde van de t-verdelingstabel met α = .025 en DF w komt overeen met de vrijheidsgraden binnen de groepen van de ANOVA-tabel.
- MS W : gemiddelde kwadraten binnen groepen in de ANOVA-tabel.
- n 1 , n 2 : De steekproefomvang van elke groep
Vervolgens kunnen we het gemiddelde verschil tussen elke groep vergelijken met deze teststatistiek. Als de absolute waarde van het gemiddelde verschil tussen twee groepen groter is dan de teststatistiek, kunnen we stellen dat er een statistisch significant verschil is tussen de groepsgemiddelden.
Het volgende voorbeeld laat zien hoe u de minst significante verschiltest van Fisher in de praktijk kunt uitvoeren.
Voorbeeld: Fisher-test voor kleinste significantieverschil
Stel dat een hoogleraar wil weten of drie verschillende studietechnieken wel of niet tot verschillende toetsscores onder studenten leiden. Om dit te testen wijst ze willekeurig 10 studenten toe om elke studietechniek te gebruiken en registreert ze hun examenresultaten.
De volgende tabel toont de examenresultaten van elke student op basis van de gebruikte studietechniek:

De professor voert een one-way ANOVA uit en bekomt de volgende resultaten:
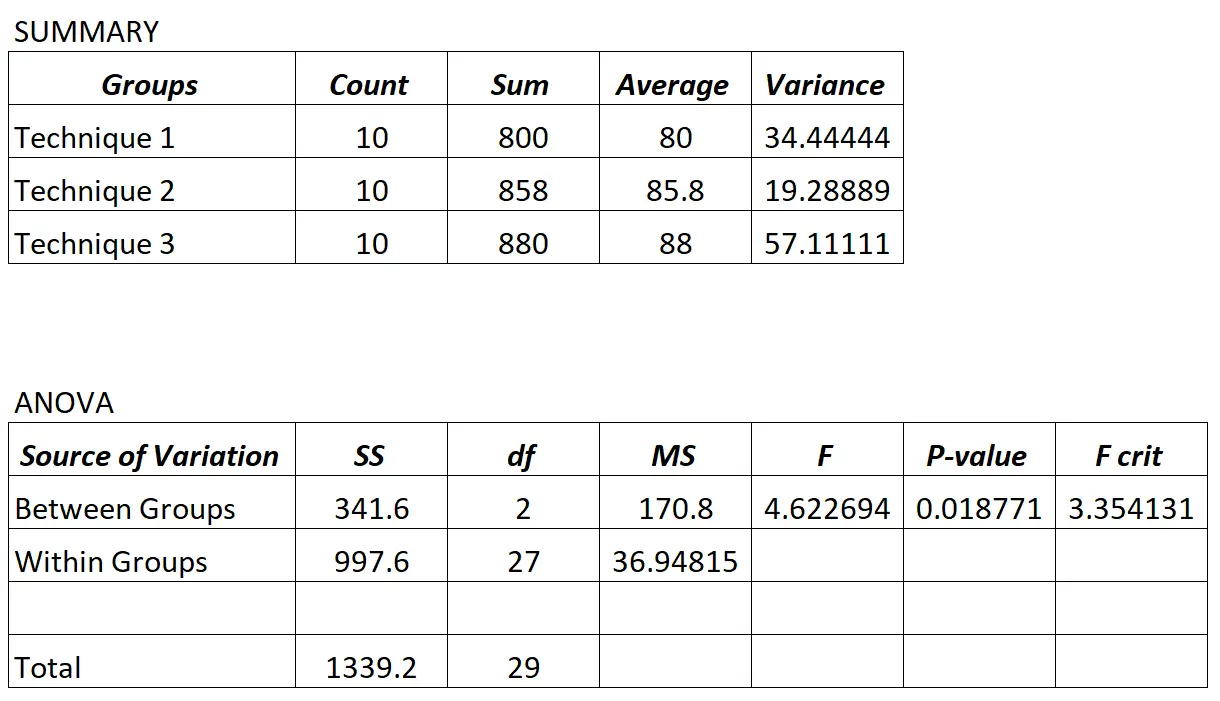
Omdat de p-waarde in de ANOVA-tabel (0,018771) kleiner is dan 0,05, kunnen we concluderen dat niet alle gemiddelde examenscores tussen de drie groepen gelijk zijn.
We kunnen dus de minst significante verschiltest van Fisher uitvoeren om te bepalen welke groepsgemiddelden verschillend zijn.
Met behulp van de waarden uit het ANOVA-resultaat kunnen we de Fisher-teststatistiek als volgt berekenen:
- LSD = t 0,025 , DFw * √ MS W (1/n 1 + 1/n 1 )
- LSD = t 0,025 , 27 * √ 36,948*(1/10 + 1/10)
- LSD = 2,052 * √ 7,3896
- LSD = 5,578
We kunnen dan het absolute gemiddelde verschil tussen elke groep berekenen:
- Techniek 1 versus Techniek 2: |80 – 85,8| = 5,8
- Techniek 1 versus Techniek 3: |80 – 88| = 8
- Techniek 2 versus Techniek 3: |85,8 – 88| = 2,2
De absolute gemiddelde verschillen tussen techniek 1 en techniek 2 en tussen techniek 1 en techniek 3 zijn groter dan de Fisher-teststatistieken. We kunnen dus concluderen dat deze technieken leiden tot statistisch significant verschillende gemiddelde examenscores.
Ook kunnen we concluderen dat er geen significant verschil is in gemiddelde examenscores tussen techniek 2 en techniek 3.