Mle voor een poisson-verdeling (stap voor stap)

Maximale waarschijnlijkheidsschatting (MLE) is een methode die kan worden gebruikt om de parameters van een bepaalde verdeling te schatten.

In deze tutorial wordt uitgelegd hoe u de MLE voor de parameter λ van een Poisson-verdeling berekent.

Stap 1: Schrijf de PDF.

Schrijf eerst de kansdichtheidsfunctie van de Poisson-verdeling:

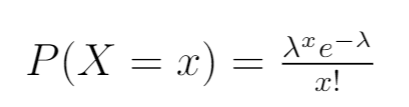
Stap 2: Schrijf de waarschijnlijkheidsfunctie.

Schrijf vervolgens de waarschijnlijkheidsfunctie. Dit is simpelweg het product van de PDF voor de waargenomen waarden x ₁ , …, x _n .

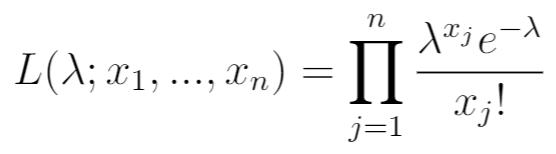
Stap 3: Schrijf de waarschijnlijkheidsfunctie van de natuurlijke logaritme.

Om de berekeningen te vereenvoudigen, kunnen we de natuurlijke waarschijnlijkheidsfunctie schrijven:

Stap 4: Bereken de afgeleide van de natuurlijke waarschijnlijkheidsfunctie met betrekking tot λ.

Vervolgens kunnen we de afgeleide van de natuurlijke waarschijnlijkheidsfunctie berekenen met betrekking tot de parameter λ:

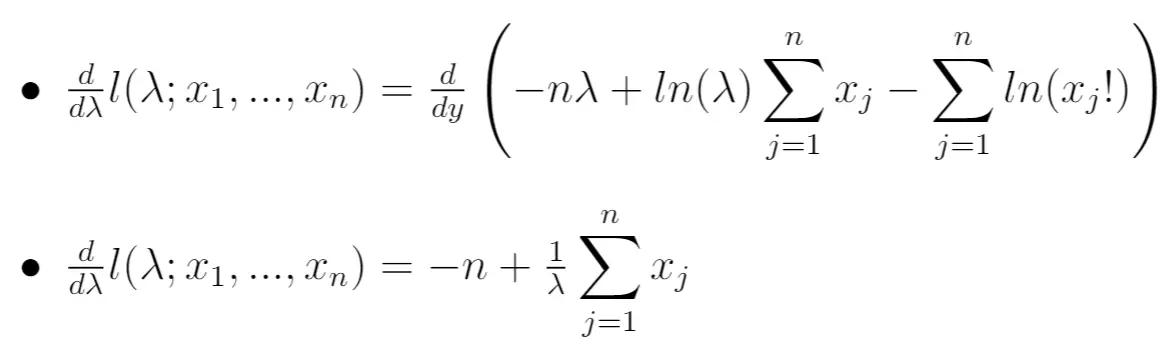
Stap 5: Stel de afgeleide gelijk aan nul en los λ op.

Ten slotte stellen we de afgeleide van de vorige stap gelijk aan nul en lossen we eenvoudigweg op voor λ:

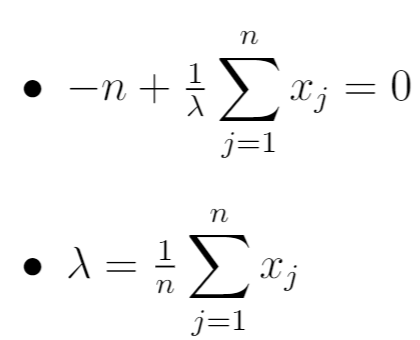
De MLE blijkt dus:

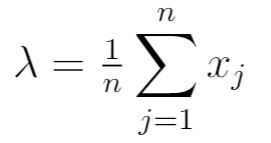
Dit komt overeen met het steekproefgemiddelde van de n waarnemingen in de steekproef.

Aanvullende bronnen

Een inleiding tot de Poisson-verdeling
Visdistributiecalculator
Hoe Poisson-distributie in Excel te gebruiken