Het monty hall-probleem: een eenvoudige visuele uitleg

In een oude spelshow genaamd Let’s Make a Deal presenteerde presentator Monty Hall de deelnemers drie deuren.

Eén van de deuren bevatte een prijs, de andere twee niet.

Monty vroeg de deelnemer om te kiezen welke deur volgens hem de prijs bevatte.

Zodra de deelnemer een deur had uitgekozen, opende Monty een deur waar de prijs niet in zat .

De prijs bleef in een van de twee gesloten deuren liggen.

Monty vroeg de kandidaat dan of hij van deur wilde veranderen.

Hoewel het misschien moeilijk te geloven lijkt, blijkt dat het wisselen van deuren op dit punt in het spel je feitelijk een grotere kans geeft om te winnen.

Blijf lezen om erachter te komen waarom!

Het Monty Hall-probleem visueel uitgelegd

Om te illustreren waarom het veranderen van deuren u een grotere kans geeft om te winnen, kunt u de volgende scenario’s overwegen waarin u eerst deur 1 kiest.

Scenario 1: Je kiest voor deur 1 en de prijs staat daadwerkelijk achter deur 1.

In dit geval zal Monty deur 2 of 3 openen en laten zien dat er achter geen van beide deuren iets zit. Blijf je bij deur 1, dan win je .

Scenario 2: Je kiest voor deur 1 en de prijs staat daadwerkelijk achter deur 2.

In dit geval moet Monty deur 3 openen en laten zien dat er niets achter zit. Als je bij deur 1 blijft, verlies je .

Scenario 3: Je kiest voor deur 1 en de prijs staat daadwerkelijk achter deur 3.

In dit geval moet Monty deur 2 openen en laten zien dat er niets achter zit. Als je bij deur 1 blijft, verlies je .

Dit zijn allemaal mogelijke uitkomsten als je voor deur 1 kiest. Let op: als je bij deur 1 blijft, bespaar je slechts een derde van de tijd. Maar als u overstapt, bespaart u tweederde van de tijd.

De volgende tabel vat alle mogelijke scenario’s in deze spelshow samen, evenals de resultaten die verband houden met onderhoud en verandering:

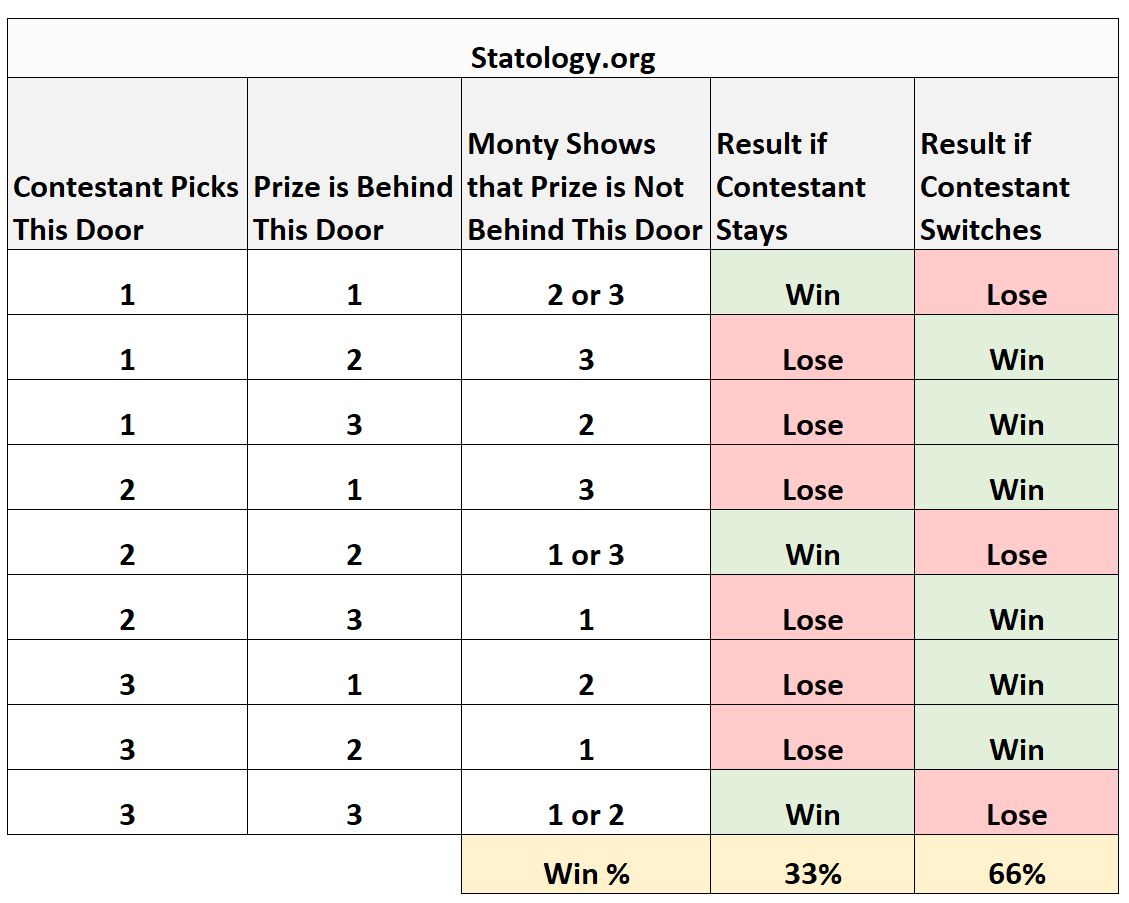
Uit de tabel kunnen we zien dat u 33% van de tijd wint als u blijft, maar dat u 66% van de tijd wint als u overstapt.

Het veranderen van deuren vergroot dus de kans dat u de prijs wint.

Hoewel dit intuïtief misschien niet logisch lijkt, liegt de wiskunde niet.