Wat is morans zelf? (definitie & #038; voorbeeld)

Moran’s I is een manier om ruimtelijke autocorrelatie te meten.

Simpel gezegd is het een manier om te kwantificeren hoe dicht waarden geclusterd zijn in de 2D-ruimte. Het wordt vaak gebruikt in de geografie en de geografische informatiewetenschap (GIS) om te meten hoe nauw verschillende kenmerken op een kaart zijn gegroepeerd, zoals gezinsinkomen, opleidingsniveau, enz.

Moran’s I: de formule

De formule om Moran’s I te berekenen is:

ik = (N/W)*ΣΣw _ij (x _ik – x )(x _j – x )/Σ(x _ik – x ) ²

Goud:

• N: Het aantal ruimtelijke eenheden geïndexeerd door i en j
• W: De som van alle _wij
• x: De rentevariabele (huishoudinkomen, jaren scholing, etc.)
• x : Het gemiddelde van x
• _wij : Een matrix van ruimtelijke gewichten

U zult deze meting waarschijnlijk nooit met de hand hoeven te berekenen, aangezien de meeste statistische software deze voor u kan berekenen, maar het helpt om de formule te kennen die onder de motorkap wordt gebruikt.

De waarde van Moran’s I kan variëren van -1 tot 1 waarbij:

• -1: De relevante variabele is perfect verspreid
• 0: de relevante variabele is willekeurig verspreid
• 1: De relevante variabele is perfect gegroepeerd

Naast het berekenen van Moran’s I berekent de meeste statistische software een overeenkomstige p-waarde die kan worden gebruikt om te bepalen of de gegevens willekeurig verspreid zijn of niet.

De Moran-test gebruikt de volgende nul- en alternatieve hypothesen:

Nulhypothese (H ₀ ): de gegevens zijn willekeurig verspreid.

Alternatieve hypothese ( _HA ): Gegevens zijn niet willekeurig verspreid, dat wil zeggen dat ze in zichtbare patronen zijn gegroepeerd.

Als de p-waarde die overeenkomt met Moran’s I onder een bepaald significantieniveau ligt (dat wil zeggen α = 0,05), dan kunnen we de nulhypothese verwerpen en concluderen dat de gegevens ruimtelijk geclusterd zijn zodat het onwaarschijnlijk is dat ze ruimtelijk geclusterd zijn. toevallig gebeurd.

Moran’s I: enkele voorbeelden

De volgende voorbeelden vertegenwoordigen valse kaarten met verschillende waarden voor Moran’s I.

Laten we aannemen dat elk vierkant op de kaart een provincie vertegenwoordigt, en dat provincies met een gemiddeld gezinsinkomen van meer dan $ 50.000 in blauw worden weergegeven.

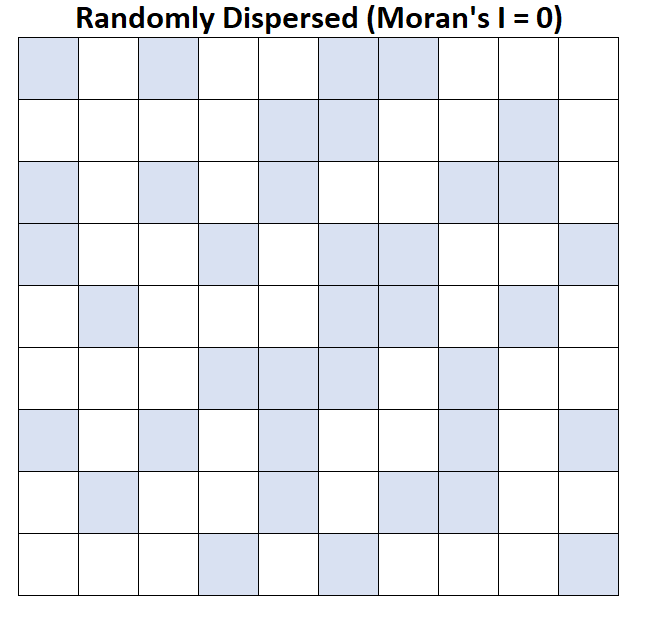
Moran’s I = 0: Het gemiddelde gezinsinkomen is willekeurig verspreid (dwz willekeurige clusters in willekeurige gebieden).

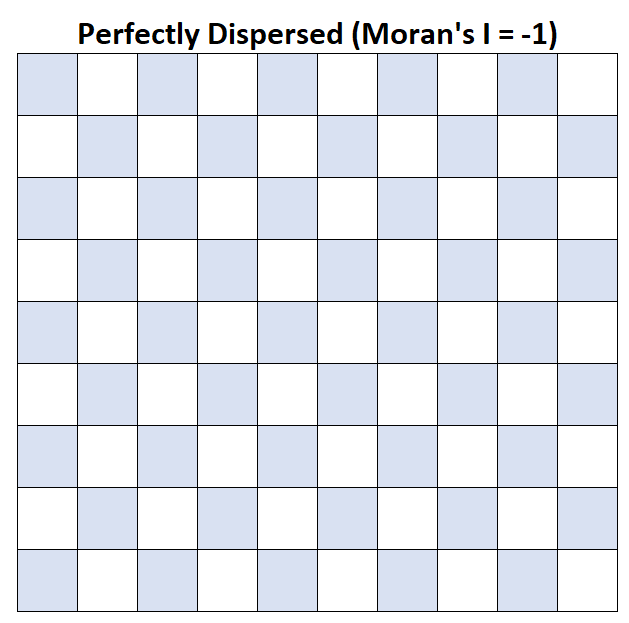
Moran’s I = -1: Het gemiddelde gezinsinkomen is perfect verspreid.

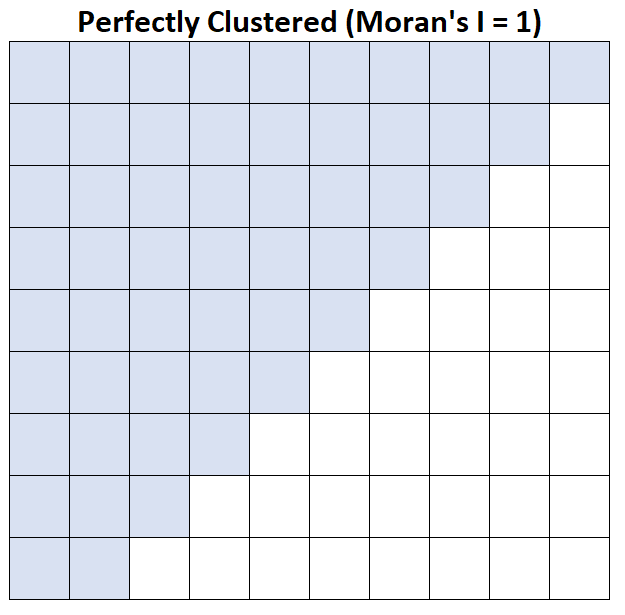
Moran’s I = 1: het gemiddelde gezinsinkomen is perfect gegroepeerd.

Raadpleeg dit voorbeeld voor een concreet voorbeeld van het berekenen van Moran’s I in de statistische software R.