Hoe te testen op multicollineariteit in stata

Multicollineariteit bij regressieanalyse treedt op wanneer twee of meer verklarende variabelen sterk met elkaar gecorreleerd zijn, zodat ze geen unieke of onafhankelijke informatie verschaffen in het regressiemodel. Als de mate van correlatie tussen variabelen hoog genoeg is, kan dit problemen veroorzaken bij het aanpassen en interpreteren van het regressiemodel.

Stel dat u meerdere lineaire regressies uitvoert met de volgende variabelen:

Variabele respons: maximale verticale sprong

Verklarende variabelen: schoenmaat, lengte, tijd besteed aan oefenen

In dit geval zijn de verklarende variabelen schoenmaat en lengte waarschijnlijk sterk gecorreleerd, aangezien lange mensen doorgaans grotere schoenmaten hebben. Dit betekent dat multicollineariteit waarschijnlijk een probleem zal zijn bij deze regressie.

Gelukkig is het mogelijk om multicollineariteit te detecteren met behulp van een metriek genaamd variantie-inflatiefactor (VIF) , die de correlatie en sterkte van de correlatie tussen verklarende variabelen in een regressiemodel meet.

In deze tutorial wordt uitgelegd hoe u VIF kunt gebruiken om multicollineariteit te detecteren in een regressieanalyse in Stata.

Voorbeeld: multicollineariteit in Stata

Voor dit voorbeeld gebruiken we de ingebouwde dataset van Stata, genaamd auto . Gebruik de volgende opdracht om de gegevensset te laden:

automatisch gebruiken

We zullen het regressiecommando gebruiken om een meervoudig lineair regressiemodel te fitten, waarbij prijs als responsvariabele en gewicht, lengte en mpg als verklarende variabelen worden gebruikt:

regressie prijs gewicht lengte mpg

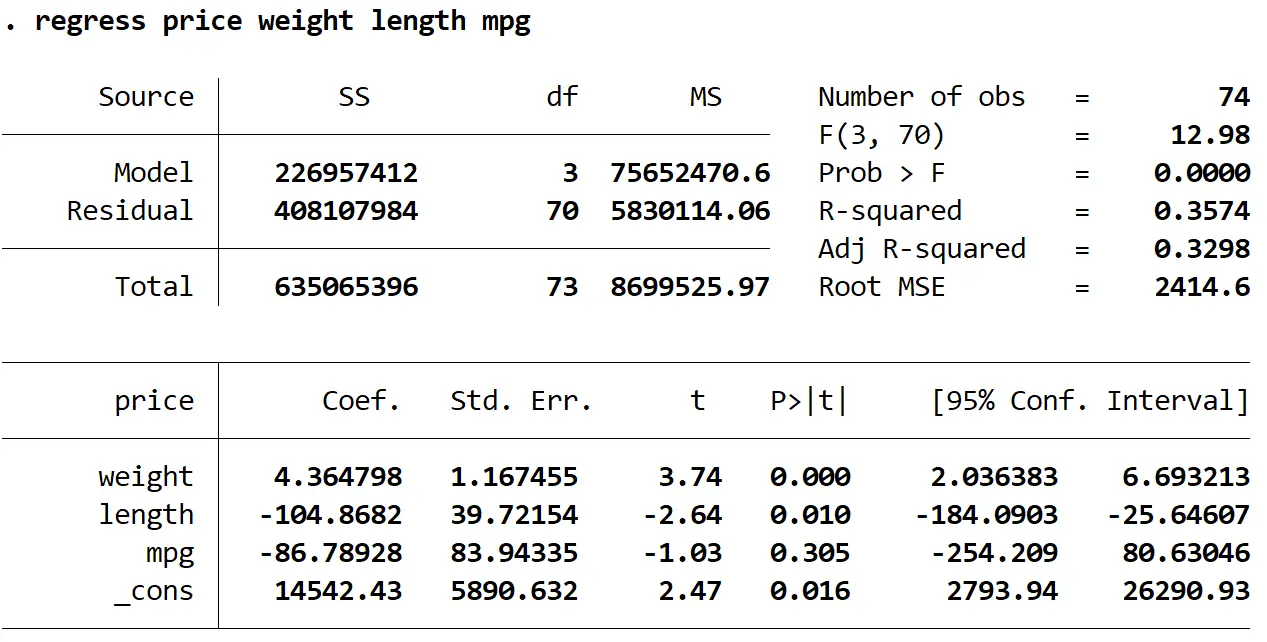
Vervolgens zullen we het vive- commando gebruiken om te testen op multicollineariteit:

levendig

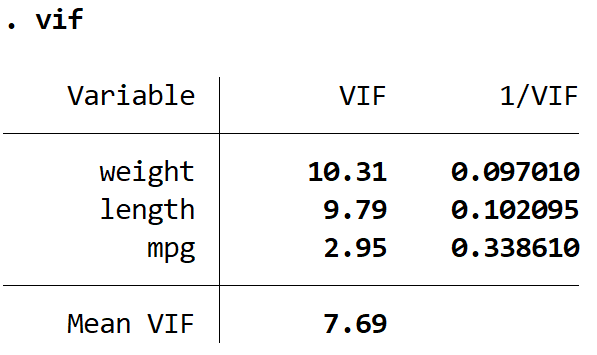
Dit levert een VIF-waarde op voor elk van de verklarende variabelen in het model. De VIF-waarde begint bij 1 en heeft geen bovengrens. Een algemene regel voor het interpreteren van VIF’s is:

• Een waarde van 1 geeft aan dat er geen correlatie bestaat tussen een bepaalde verklarende variabele en enige andere verklarende variabele in het model.
• Een waarde tussen 1 en 5 duidt op een gematigde correlatie tussen een bepaalde verklarende variabele en andere verklarende variabelen in het model, maar deze is vaak niet ernstig genoeg om speciale aandacht te vereisen.
• Een waarde groter dan 5 duidt op een potentieel ernstige correlatie tussen een bepaalde verklarende variabele en andere verklarende variabelen in het model. In dit geval zijn de coëfficiëntschattingen en p-waarden in de regressieresultaten waarschijnlijk onbetrouwbaar.

We kunnen zien dat de VIF-waarden voor gewicht en lengte groter zijn dan 5, wat aangeeft dat multicollineariteit waarschijnlijk een probleem is in het regressiemodel.

Hoe om te gaan met multicollineariteit

Vaak is de eenvoudigste manier om met multicollineariteit om te gaan het eenvoudigweg verwijderen van een van de probleemvariabelen, omdat de variabele die u verwijdert waarschijnlijk sowieso overbodig is en weinig unieke of onafhankelijke informatie aan het model toevoegt.

Om te bepalen welke variabele we moeten verwijderen, kunnen we het corr- commando gebruiken om een correlatiematrix te maken om de correlatiecoëfficiënten tussen elk van de variabelen in het model weer te geven, wat ons kan helpen identificeren welke variabelen sterk met elkaar gecorreleerd kunnen zijn en de oorzaak kunnen zijn van de probleem van multicollineariteit:

corr prijs gewicht lengte mpg

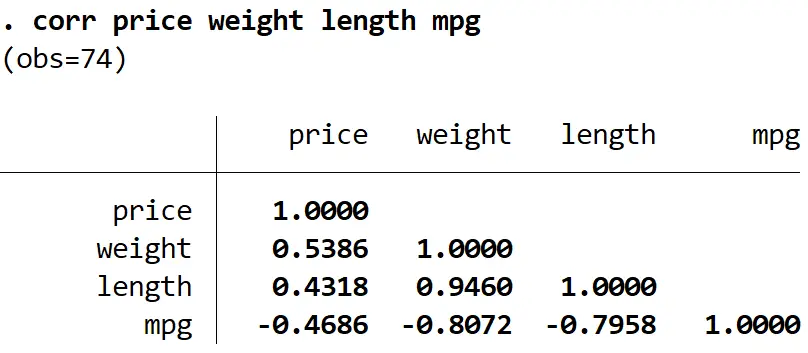
We kunnen zien dat lengte sterk gecorreleerd is met zowel gewicht als mpg, en de laagste correlatie heeft met de responsvariabele prijs. Het verwijderen van de modellengte zou dus het multicollineariteitsprobleem kunnen oplossen zonder de algehele kwaliteit van het regressiemodel te verminderen.

Om dit te testen, kunnen we de regressieanalyse opnieuw uitvoeren met alleen gewicht en mpg als verklarende variabelen:

regressie prijs gewicht mpg

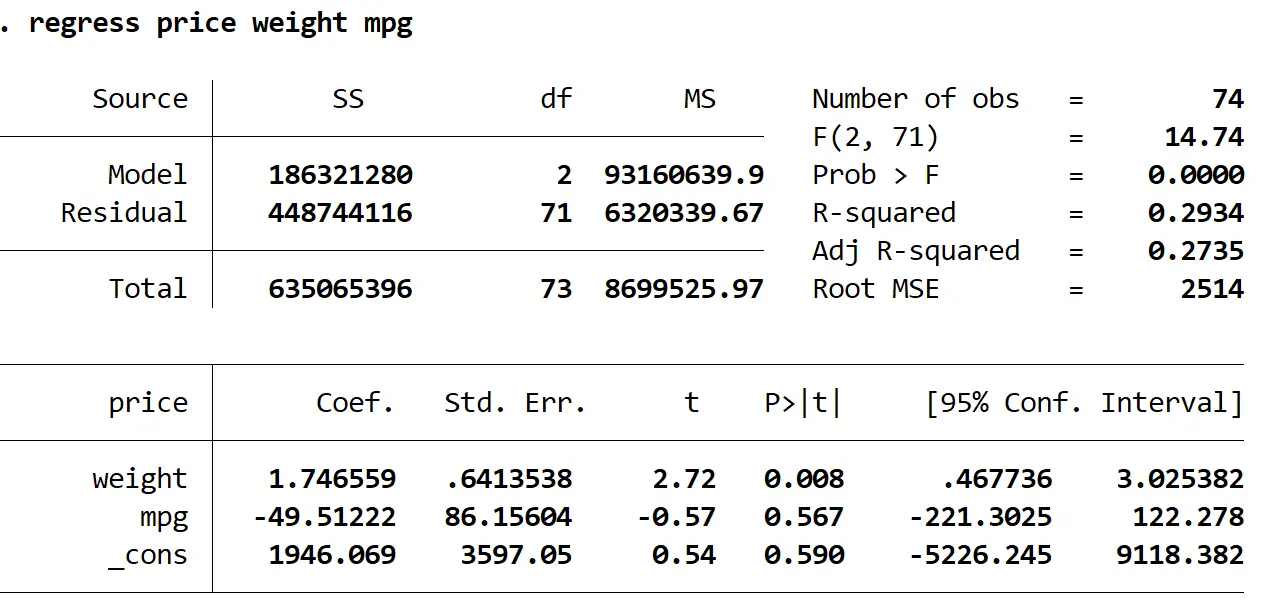
We kunnen zien dat het aangepaste R-kwadraat van dit model 0,2735 is, vergeleken met 0,3298 in het vorige model. Dit geeft aan dat de algehele bruikbaarheid van het model slechts licht is afgenomen. Vervolgens kunnen we de VIF-waarden vinden met behulp van de VIF- opdracht:

LEVENDIG

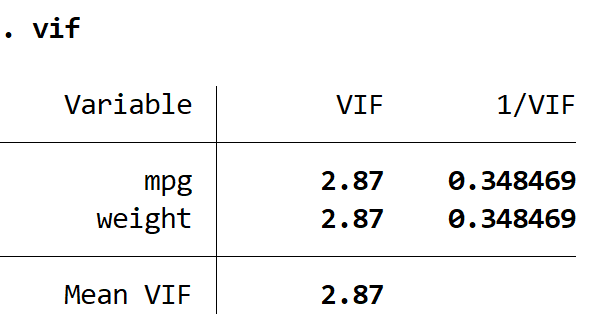
Beide VIF-waarden zijn kleiner dan 5, wat aangeeft dat multicollineariteit geen probleem meer is in het model.