Wat is een multimodale distributie?

Een multimodale verdeling is een kansverdeling met twee of meer modi.

Als u een histogram maakt om een multimodale verdeling te visualiseren, zult u merken dat deze verschillende pieken heeft:

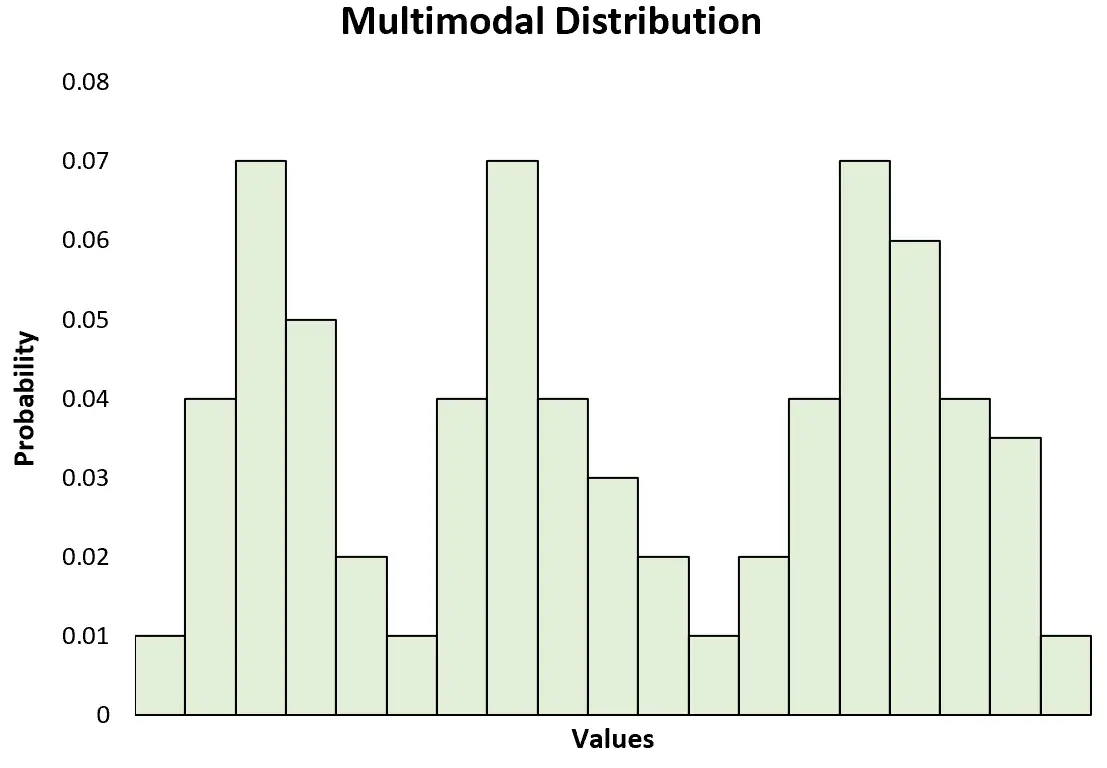
Als een distributie precies twee pieken heeft, wordt deze beschouwd als een bimodale distributie , wat een specifiek type multimodale distributie is.

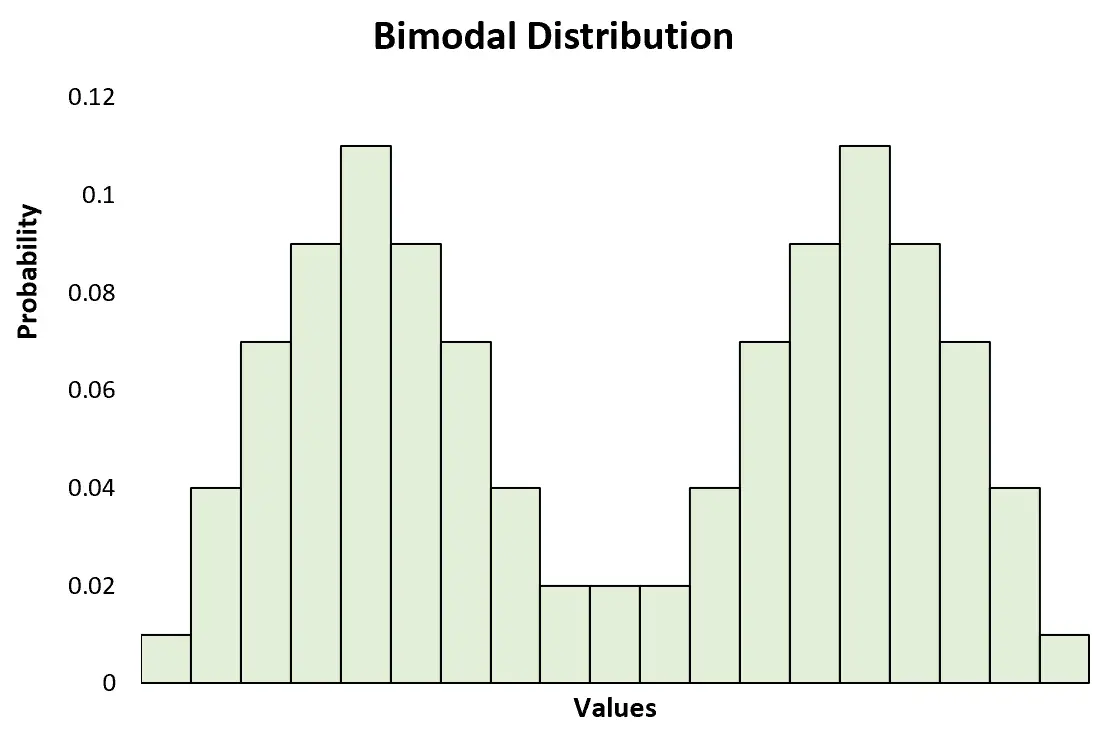
Dit staat in contrast met een unimodale verdeling, die slechts één piek heeft:

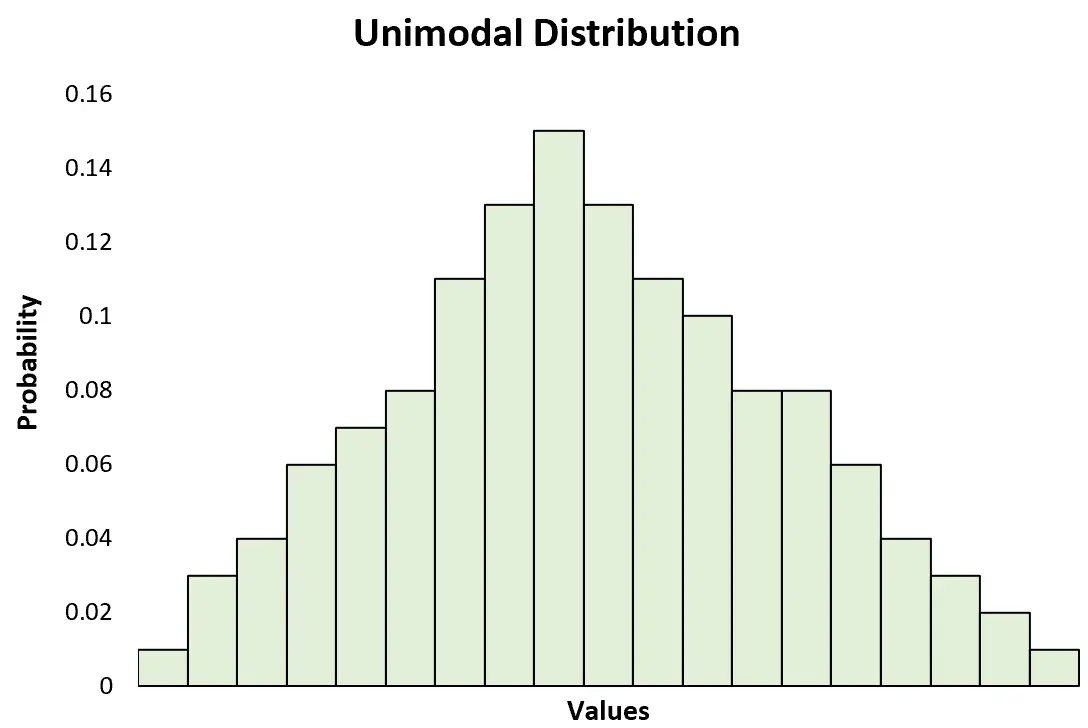
Hoewel unimodale verdelingen zoals de normale verdeling het vaakst worden gebruikt om onderwerpen in de statistiek uit te leggen, komen multimodale verdelingen in de praktijk vrij vaak voor, dus het is nuttig om te weten hoe u ze kunt herkennen en analyseren.

Voorbeelden van multimodale distributies

Hier zijn enkele voorbeelden van multimodale distributies.

Voorbeeld 1: Verdeling van examenresultaten

Stel dat een professor een examen aflegt aan zijn klas. Sommige studenten studeerden, anderen niet. Wanneer de professor een histogram van examenscores maakt, volgt deze een multimodale verdeling met een piek rond lage scores voor studenten die niet hebben gestudeerd en een andere piek rond hoge scores voor studenten die wel hebben gestudeerd:

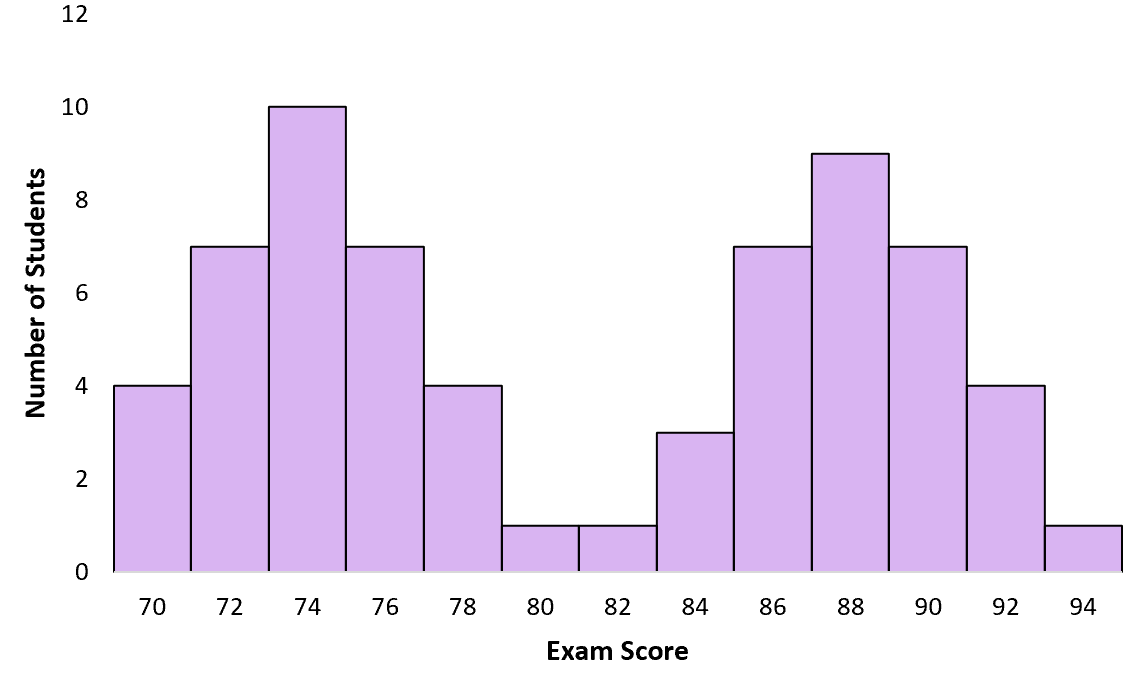
Voorbeeld 2: Hoogte van verschillende plantensoorten

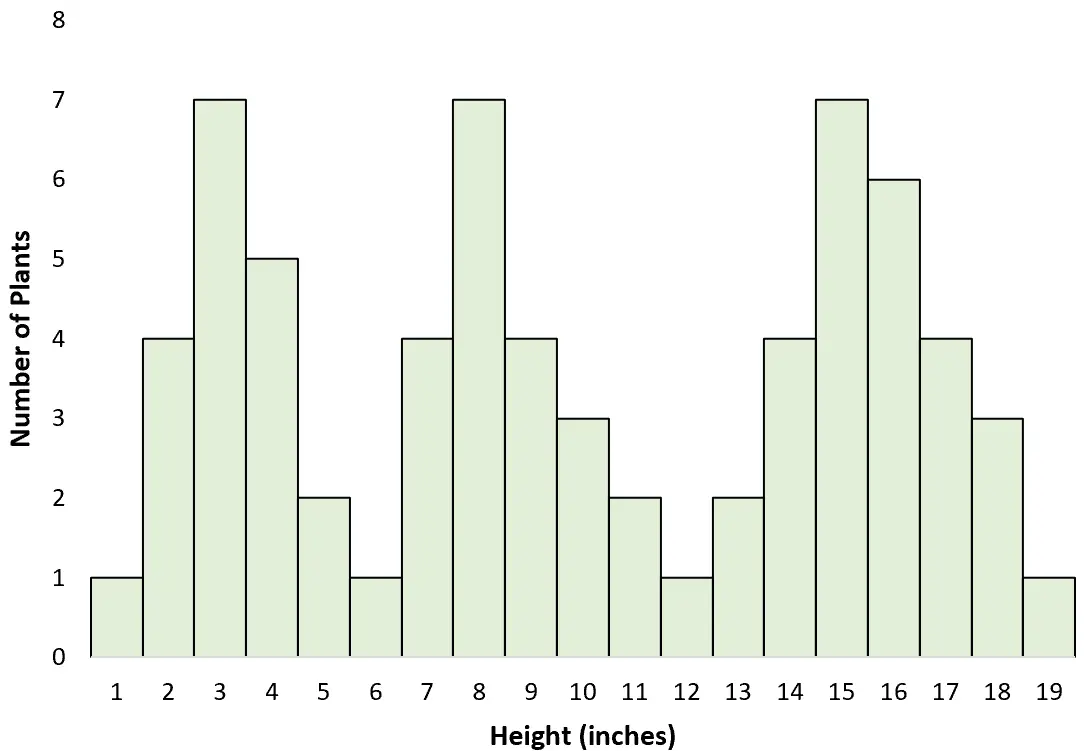
Stel dat een wetenschapper door een veld loopt en de hoogte van verschillende planten meet. Zonder het te beseffen meet ze de grootte van drie verschillende soorten: de ene vrij groot, de andere middelgroot en nog een vrij klein.

Wanneer ze een histogram maakt om de hoogteverdeling te visualiseren, ontdekt ze dat deze multimodaal is: elke piek vertegenwoordigt de meest voorkomende hoogte van de drie verschillende soorten.

Voorbeeld 3: Verdeling van klanten

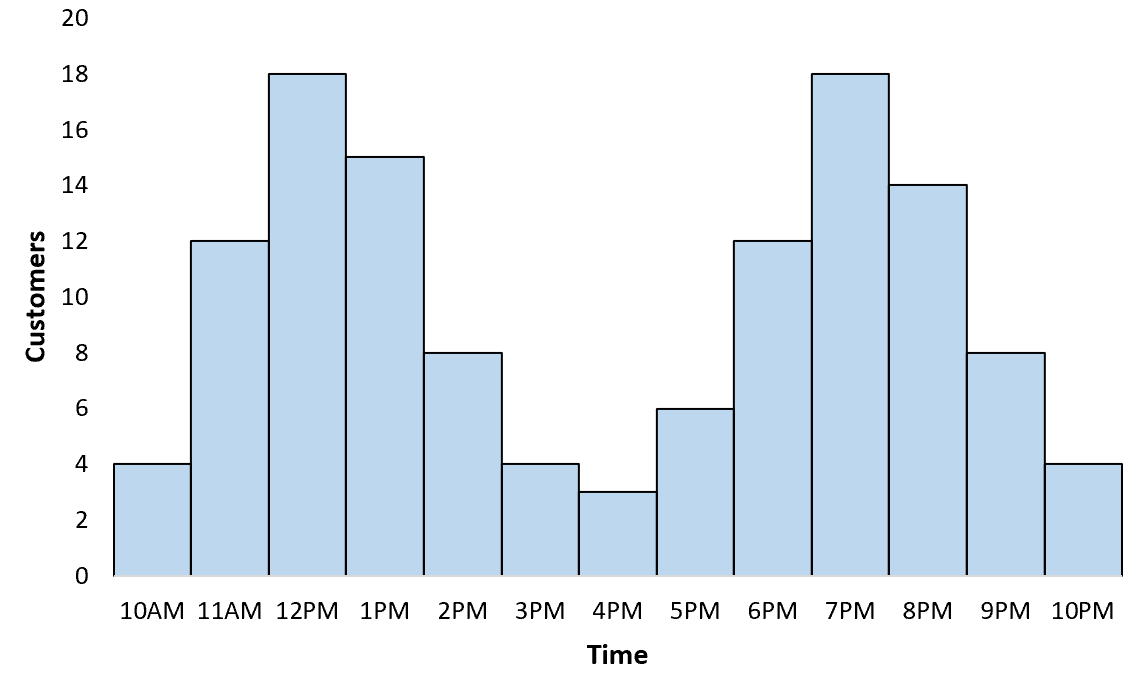
Een restauranteigenaar houdt bij hoeveel klanten er elk uur komen. Wanneer hij een histogram maakt om de distributie van klanten in beeld te brengen, ziet hij dat de distributie multimodaal is: er is een piek tijdens de lunch en nog een piek tijdens de dineruren.

Wat zijn de oorzaken van multimodale distributies?

Er zijn gewoonlijk een van de twee oorzaken die ten grondslag liggen aan multimodale distributies:

1. Verschillende groepen zijn gegroepeerd.

Multimodale distributies kunnen optreden wanneer u gegevens verzamelt voor meerdere groepen zonder dat u het zich realiseert.

Als een wetenschapper bijvoorbeeld onbewust de hoogte meet van drie verschillende plantensoorten die zich in hetzelfde veld bevinden, zal de verdeling van alle planten multimodaal lijken wanneer ze op hetzelfde histogram worden geplaatst.

2. Er is een onderliggend fenomeen.

Multimodale distributies kunnen ook optreden als gevolg van bepaalde onderliggende verschijnselen.

Het aantal klanten dat elk uur een restaurant bezoekt, volgt bijvoorbeeld een multimodale verdeling, aangezien mensen de neiging hebben om op twee verschillende tijdstippen in restaurants te eten: lunch en diner. Dit onderliggende menselijke gedrag is de oorsprong van multimodale distributie.

Hoe multimodale distributies te analyseren

We beschrijven verdelingen vaak met behulp van het gemiddelde of de mediaan , omdat dit ons een idee geeft van waar het ‘centrum’ van de verdeling zich bevindt.

Helaas zijn het gemiddelde en de mediaan niet nuttig om te weten voor een bimodale verdeling. De gemiddelde examenscore van de studenten in bovenstaand voorbeeld is bijvoorbeeld 81:

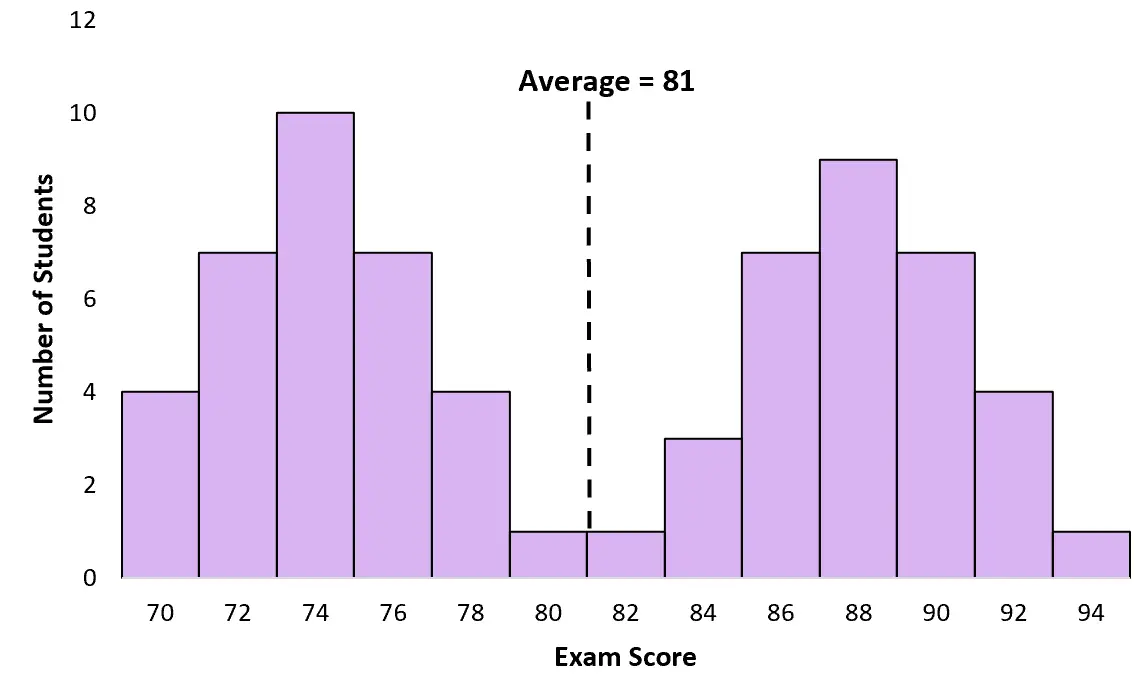
Er zijn echter maar heel weinig studenten die in de buurt van de 81 scoren. In dit geval is het gemiddelde misleidend. De meeste studenten scoorden feitelijk rond de 74 of 88.

Een betere manier om bimodale verdelingen te analyseren en interpreteren is om de gegevens simpelweg in twee afzonderlijke groepen te verdelen en vervolgens de centrumlocatie en verdeling voor elke groep afzonderlijk te analyseren.

We kunnen examenresultaten bijvoorbeeld verdelen in ‚lage scores‘ en ‚hoge scores‘ en vervolgens voor elke groep het gemiddelde en de standaarddeviatie vinden.

Wanneer u samenvattende statistieken berekent voor een bepaalde verdeling, zoals het gemiddelde, de mediaan of de standaarddeviatie, zorg er dan voor dat u de verdeling visualiseert om te bepalen of deze unimodaal of multimodaal is.

Als een verdeling multimodaal is, kan het misleidend zijn om deze te beschrijven met behulp van één gemiddelde, mediaan of standaarddeviatie.