Wat is een multinomiale test? (definitie & #038; voorbeeld)

Een multinomiale test wordt gebruikt om te bepalen of een categorische variabele een hypothetische verdeling volgt.

Deze test maakt gebruik van de volgende nul- en alternatieve hypothesen :

H ₀ : Een categorische variabele volgt een hypothetische verdeling.

H _A : Een categorische variabele volgt niet de hypothetische verdeling.

Als de p-waarde van de test onder een bepaald significantieniveau ligt (bijvoorbeeld α = 0,05), kunnen we de nulhypothese verwerpen en concluderen dat de variabele niet de veronderstelde verdeling volgt.

Deze test wordt gebruikt wanneer een variabele k verschillende resultaten kan opleveren. Een klassiek voorbeeld van een multinomiale test is waarbij we willen bepalen of bepaalde dobbelstenen eerlijk zijn. Wanneer u een dobbelsteen gooit, is de kans dat deze op elk getal (1 tot en met 6) valt 1/6.

Om te testen of een dobbelsteen eerlijk is, kunnen we deze een aantal keren gooien en kijken of het aantal keren dat hij op verschillende getallen terechtkomt aanzienlijk verschilt van wat we zouden verwachten.

De volgende voorbeelden laten zien hoe u een multinomiale test uitvoert met behulp van de statistische programmeertaal R.

Voorbeeld 1: Eerlijke dobbelstenen

Stel dat we willen bepalen of een dobbelsteen eerlijk is. Om dit te testen, voeren we het 30 keer uit en registreren we de frequentie van elk resultaat. De volgende tabel toont de resultaten:

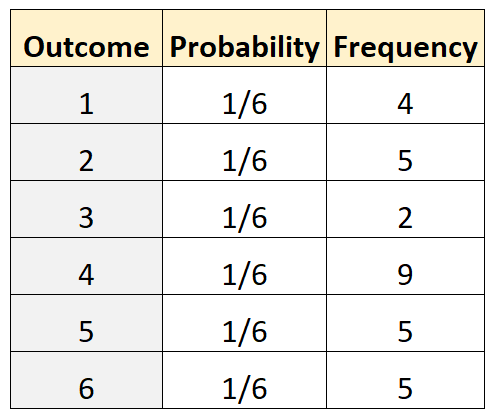
De volgende code in R kan worden gebruikt om een multinomiale test uit te voeren:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

De p-waarde van de test is 0,4306 . Omdat deze p-waarde niet kleiner is dan 0,05, zullen we de nulhypothese niet verwerpen. We hebben dus niet genoeg bewijs om te zeggen dat de dobbelstenen oneerlijk zijn.

Voorbeeld 2: Productverkoop

Stel dat een winkeleigenaar veronderstelt dat een gelijk aantal klanten elk van de vier verschillende producten zal kopen. Om dit te testen, registreert het het aantal klanten dat elk product in een bepaalde week heeft gekocht. De volgende tabel toont de resultaten:

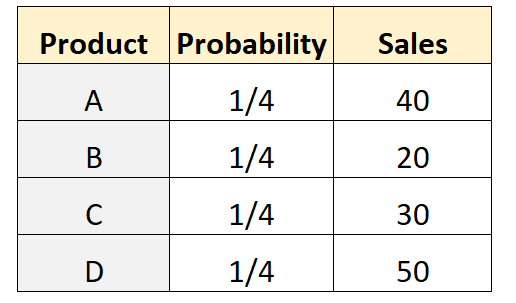
De volgende code in R kan worden gebruikt om een multinomiale test op deze dataset uit te voeren:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

De p-waarde van de test is 0,00226 . Omdat deze p-waarde kleiner is dan 0,05, zullen we de nulhypothese verwerpen. We hebben dus genoeg bewijs om te zeggen dat de verkoop niet voor elk product gelijk is.

Voorbeeld 3: Knikkers in een zakje

Tom stelt dat de kans dat je een rode, groene of paarse knikker uit een zakje kiest respectievelijk 0,2, 0,5 en 0,3 is. Om dit te testen, reikt zijn vriend Mike in de zak en haalt er 100 keer een knikker (met vervangingen) uit. De volgende tabel toont de resultaten:

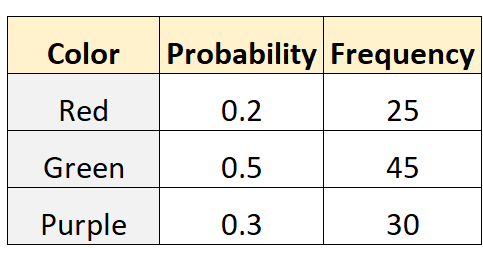
De volgende code in R kan worden gebruikt om een multinomiale test op deze dataset uit te voeren:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

De p-waarde van de test is 0,3999 . Omdat deze p-waarde niet kleiner is dan 0,05, zullen we er niet in slagen de nulhypothese te verwerpen. We hebben daarom niet genoeg bewijs om te zeggen dat de verdeling van de knikkers in de zak anders is dan aangegeven door Tom.

Aanvullende bronnen

Een inleiding tot multinomiale distributie
Multinomiale distributiecalculator