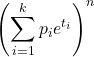Multinomiale distributie

Von Dr.benjamin anderson August 4, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat een multinomiale verdeling in de statistiek is. U zult dus de definitie van een multinomiale verdeling vinden, wat de formule is, een opgeloste oefening en wat de eigenschappen zijn van dit type kansverdeling. Bovendien kunt u de waarschijnlijkheid van een multinomiale verdeling berekenen met een online calculator.

Wat is een multinomiale verdeling?

De multinomiale verdeling (of multinomiale verdeling ) is een waarschijnlijkheidsverdeling die de waarschijnlijkheid beschrijft dat verschillende elkaar uitsluitende gebeurtenissen na verschillende pogingen een bepaald aantal keren voorkomen.

Dat wil zeggen, als een willekeurig experiment kan resulteren in drie of meer exclusieve gebeurtenissen en de waarschijnlijkheid dat elke gebeurtenis afzonderlijk plaatsvindt bekend is, wordt de multinomiale verdeling gebruikt om de waarschijnlijkheid te berekenen dat wanneer meerdere experimenten worden uitgevoerd, een bepaald aantal gebeurtenissen plaatsvindt. keer elke keer.

De multinomiale verdeling is daarom een generalisatie van de binominale verdeling.

Multinomiale distributieformule

Om een multinomiale verdelingskans te berekenen, moet u eerst het quotiënt bepalen tussen de faculteit van het totale aantal gegevens en de faculteiten van het aantal keren dat elke gebeurtenis voorkomt, en het resultaat wordt vermenigvuldigd met het product van de waarschijnlijkheid van elke gebeurtenis. teruggebracht tot het aantal keren dat de genoemde gebeurtenis heeft plaatsgevonden.

Met andere woorden, de formule voor de multinomiale verdeling is als volgt:

Goud:

$P$

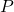
is de waarschijnlijkheid van de berekende multinomiale verdeling.
$n$

is het totaal aantal uitgevoerde tests.
$x_i$

is het aantal keren dat de gebeurtenis plaatsvindt

$i$

.
$p_i$

is de waarschijnlijkheid dat de gebeurtenis plaatsvindt

$i$

.

👉 U kunt de onderstaande rekenmachine gebruiken om de waarschijnlijkheid te berekenen van een variabele die de multinomiale verdeling volgt.

Voorbeeld van multinomiale distributie

Om uw begrip van het concept van multinomiale verdeling af te ronden, heeft u hieronder een voorbeeld opgelost van het berekenen van de waarschijnlijkheid van een multinomiale verdeling.

Een winkel verkoopt drie verschillende producten. Wanneer een klant een aankoop doet, is de kans dat het product A, product B of product C betreft respectievelijk 30%, 15% en 55%. Bereken de kans dat wanneer de winkel 8 eenheden heeft verkocht, er 2 van product A zijn, 1 van product B en 5 van product C.

Het gedefinieerde probleem wordt bepaald door een multinomiale verdeling. Daarom is het noodzakelijk om de formule voor dit type kansverdeling toe te passen:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Dus vervangen we de gegevens van het probleem in de formule en voeren de waarschijnlijkheidsberekening uit:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

De kans dat wat de probleemstelling zegt zal gebeuren, is dus 11,4%.

Multinomiale distributiecalculator

Schrijf het aantal keren dat elke gebeurtenis voorkomt in het eerste vakje en, in dezelfde volgorde, de waarschijnlijkheid dat elke gebeurtenis in het tweede vakje voorkomt. Voer vervolgens het totale aantal pogingen in de laatste lege ruimte in.

Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.

Eigenschappen van multinomiale distributie

De multinomiale verdeling heeft de volgende kenmerken:

In een multinomiale verdeling is de verwachte waarde van het aantal keren dat gebeurtenis i optreedt bij het uitvoeren van n pogingen gelijk aan het totale aantal uitgevoerde pogingen vermenigvuldigd met de waarschijnlijkheid dat de gebeurtenis optreedt.

$E[x_i]=n\cdot p_i$

In een multinomiale verdeling wordt de variantie voor gebeurtenis i berekend met behulp van de volgende uitdrukking:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

Op dezelfde manier is de covariantie tussen twee gebeurtenissen gelijk aan het product van het totale aantal pogingen vermenigvuldigd met de waarschijnlijkheid van elke gebeurtenis vermenigvuldigd met -1:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

De momentgenererende functie voor een multinomiale verdeling is:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder