Negatief binomiaal versus poisson: hoe een regressiemodel te kiezen

Negatieve binomiale regressie en Poisson-regressie zijn twee soorten regressiemodellen die moeten worden gebruikt wanneer deresponsvariabele wordt weergegeven door discrete telresultaten.

Hier volgen enkele voorbeelden van responsvariabelen die discrete telresultaten vertegenwoordigen:

• Het aantal studenten dat een bepaalde opleiding afrondt
• Het aantal verkeersongevallen op een bepaald kruispunt
• Het aantal deelnemers dat een marathon voltooit
• Het aantal retourzendingen in een bepaalde maand bij een winkel

Als de variantie ongeveer gelijk is aan het gemiddelde, past een Poisson-regressiemodel over het algemeen goed bij een dataset.

Als de variantie echter aanzienlijk groter is dan het gemiddelde, kan een negatief binomiaal regressiemodel over het algemeen beter bij de gegevens passen.

Er zijn twee technieken die we kunnen gebruiken om te bepalen of Poisson-regressie of negatieve binomiale regressie geschikter is voor een bepaalde dataset:

1. Restpercelen

We kunnen een grafiek maken van de gestandaardiseerde residuen tegen de voorspelde waarden uit een regressiemodel.

Als de meerderheid van de gestandaardiseerde residuen tussen -2 en 2 ligt, is een Poisson-regressiemodel waarschijnlijk geschikt.

Als veel residuen echter buiten dit bereik vallen, zal een negatief binomiaal regressiemodel waarschijnlijk een betere fit opleveren.

2. Test van de waarschijnlijkheidsratio

We kunnen een Poisson-regressiemodel en een negatief binomiaal regressiemodel in dezelfde dataset passen en vervolgens een waarschijnlijkheidsratiotest uitvoeren.

Als de p-waarde van de test onder een bepaald significantieniveau ligt (bijvoorbeeld 0,05), kunnen we concluderen dat het negatief binomiale regressiemodel een significant betere fit oplevert.

Het volgende voorbeeld laat zien hoe u deze twee technieken in R kunt gebruiken om te bepalen of het beter is om een Poisson-regressie- of een negatief binomiaal regressiemodel te gebruiken voor een bepaalde gegevensset.

Voorbeeld: negatieve binomiale regressie versus Poisson-regressie

Stel dat we willen weten hoeveel beurzen een honkbalspeler op een middelbare school in een bepaalde provincie ontvangt op basis van zijn schoolafdeling („A“, „B“ of „C“) en zijn schoolcijfer. toelatingsexamen voor de universiteit (gemeten van 0 tot 100). ).

Gebruik de volgende stappen om te bepalen of een negatief binomiaal regressiemodel of een Poisson-regressiemodel beter bij de gegevens past.

Stap 1: Creëer de gegevens

Met de volgende code wordt de dataset gemaakt waarmee we gaan werken, die gegevens over 1000 honkbalspelers bevat:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Stap 2: Pas een Poisson-regressiemodel en een negatief binomiaal regressiemodel aan

De volgende code laat zien hoe u zowel een Poisson-regressiemodel als een negatief binomiaal regressiemodel aan de gegevens kunt aanpassen:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Stap 3: Maak resterende plots

De volgende code laat zien hoe u restplots voor beide modellen kunt maken.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

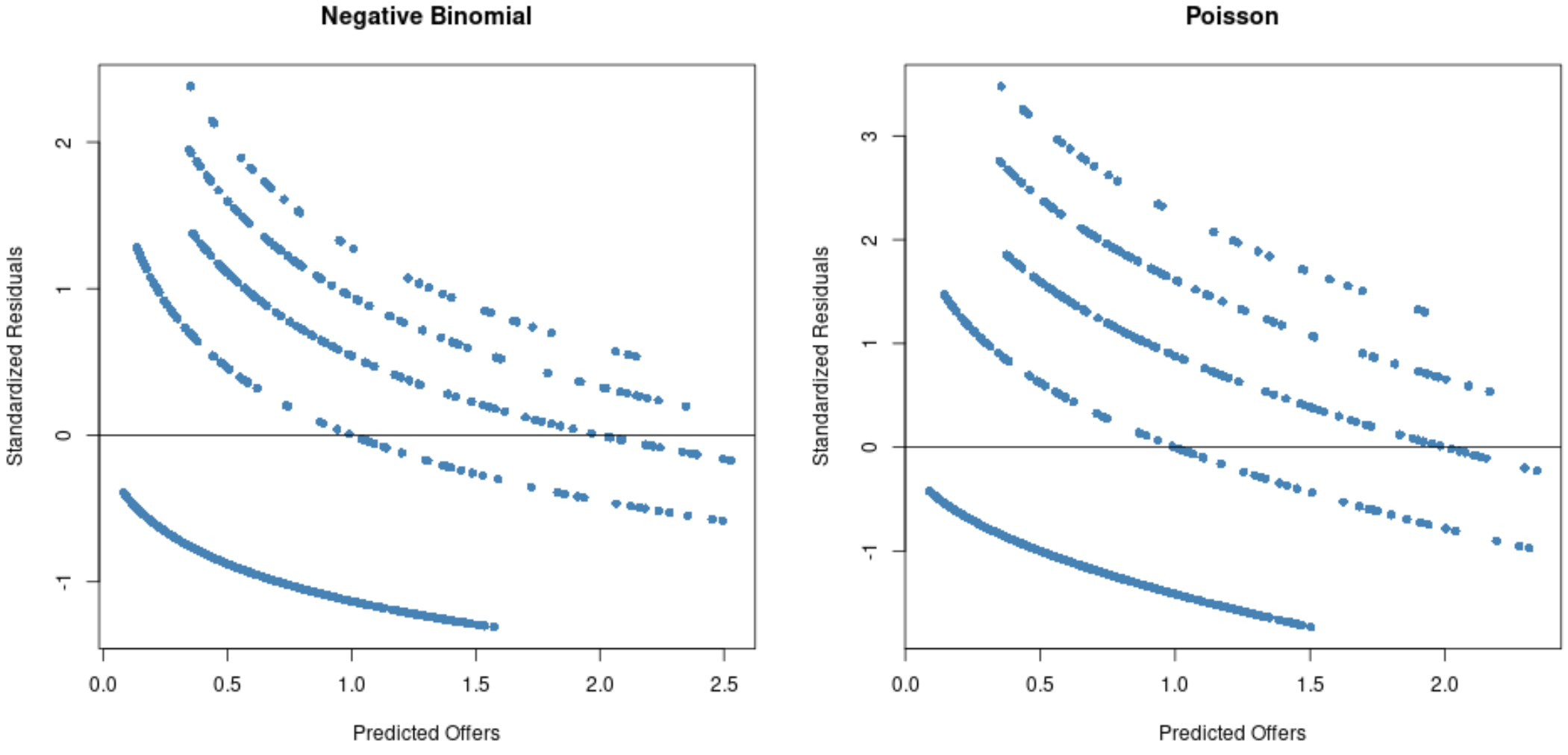
Uit de grafieken kunnen we zien dat de residuen meer verspreid zijn voor het Poisson-regressiemodel (merk op dat sommige residuen verder reiken dan 3) vergeleken met het negatief binomiale regressiemodel.

Dit is een teken dat een negatief binomiaal regressiemodel waarschijnlijk geschikter is, aangezien de residuen van dit model kleiner zijn.

Stap 4: Voer een waarschijnlijkheidsratiotest uit

Ten slotte kunnen we een waarschijnlijkheidsratiotest uitvoeren om te bepalen of er een statistisch significant verschil is in de pasvorm van de twee regressiemodellen:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

De p-waarde van de test blijkt 3,508072e-29 te zijn, wat aanzienlijk minder is dan 0,05.

We zouden dus kunnen concluderen dat het negatieve binomiale regressiemodel een significant betere fit met de gegevens oplevert vergeleken met het Poisson-regressiemodel.

Aanvullende bronnen

Een inleiding tot de negatieve binominale verdeling
Een inleiding tot de Poisson-verdeling