Negatieve binominale verdeling
In dit artikel wordt uitgelegd wat de negatieve binominale verdeling is en waarvoor deze wordt gebruikt. Ook vindt u de formule voor de negatieve binominale verdeling, een concreet voorbeeld en de eigenschappen van dit type kansverdeling. Ten slotte kunt u met een online calculator elke negatieve binomiale verdelingskans berekenen.
Wat is de negatieve binominale verdeling?
De negatieve binomiale verdeling is een waarschijnlijkheidsverdeling die het aantal Bernoulli-proeven beschrijft dat nodig is om een bepaald aantal positieve resultaten te verkrijgen.
Daarom heeft een negatieve binominale verdeling twee karakteristieke parameters: r is het aantal gewenste succesvolle uitkomsten en p is de kans op succes voor elk uitgevoerd Bernoulli-experiment.
![]()
Bedenk dat een Bernoulli-test een experiment is dat twee mogelijke uitkomsten heeft: ’succes‘ en ‚mislukking‘. Dus als de kans op ‘succes’ p is, is de kans op ‘mislukking’ q=1-p .
Een negatieve binominale verdeling definieert dus een proces waarin zoveel Bernoulli-proeven worden uitgevoerd als nodig is om positieve resultaten te verkrijgen. Bovendien zijn al deze Bernoulli-proeven onafhankelijk en hebben ze een constante kans op succes .
Een willekeurige variabele die een negatieve binominale verdeling volgt, is bijvoorbeeld het aantal keren dat een dobbelsteen moet worden gegooid totdat het getal 6 drie keer wordt gegooid.
Het verschil tussen een negatieve binomiale verdeling en een binomiale verdeling is dat de negatieve binomiale verdeling het aantal keren telt dat nodig is om een bepaald aantal succesvolle uitkomsten te verkrijgen, terwijl de binominale verdeling het aantal succesvolle gevallen in een reeks Bernoulli-tests telt.
Negatieve binomiale verdelingsformule
Gegeven de parameters r, p, x wordt de waarschijnlijkheid van een negatieve binomiale verdeling berekend door het combinatorische getal van x-1 in xr te vermenigvuldigen met (1-p) xr met p r .
De formule voor het berekenen van een negatieve binomiale verdelingskans is dus:

👉 U kunt de onderstaande rekenmachine gebruiken om de waarschijnlijkheid te berekenen van een variabele die de negatieve binominale verdeling volgt.
Opgeloste oefening van de negatieve binominale verdeling
- Wat is de kans dat als je acht keer een munt opgooit, deze bij de achtste worp voor de vierde keer kop krijgt?
Eerst moeten we de kans berekenen dat we kop krijgen bij het opgooien van een munt. In dit geval hebben we slechts één positieve uitkomst (kop) van de twee mogelijke uitkomsten (kop en munt), dus de kans op succes is:
![]()
De willekeurige variabele in dit probleem volgt dus een negatieve binominale verdeling waarbij r=4 en p=0,5. Daarom gebruiken we de formule voor de negatieve binominale verdeling om de waarschijnlijkheid te berekenen die de oefening ons vraagt.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-bc56100604e5889a6d169c0395f19ebe_l3.png)
Kenmerken van de negatieve binominale verdeling
Hieronder staan de belangrijkste kenmerken van de negatieve binominale verdeling.
- De negatieve binomiale verdeling wordt gedefinieerd door twee karakteristieke parameters: r is het aantal gewenste succesvolle resultaten en p is de kans op succes voor elk uitgevoerd Bernoulli-experiment.
*** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.
- De variantie van een negatieve binomiale verdeling is gelijk aan r vermenigvuldigd met (1-p) gedeeld door p 2 .
![]()
- Als de parameter r groter is dan 1, kan de modus van een negatieve binominale verdeling worden berekend met de volgende formule:
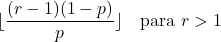
![]()
- De scheefheidscoëfficiënt van een negatieve binominale verdeling wordt berekend met de volgende uitdrukking:
![]()
- De kurtosis van een negatieve binominale verdeling kan worden gevonden met de volgende formule:
![]()
- Als de parameter r gelijk is aan 1, dan hebben we te maken met een geometrische verdeling .
![]()
Negatieve binomiale verdelingscalculator
Voer de waarden van de parameters r, p, x in de volgende rekenmachine in om de waarschijnlijkheid te berekenen. U moet getallen invoeren met de punt als decimaal scheidingsteken, bijvoorbeeld 0,50.