Hoe normalcdf-kansen in excel te berekenen

De NormalCDF- functie op een TI-83- of TI-84-rekenmachine kan worden gebruikt om de waarschijnlijkheid te bepalen dat een normaal verdeelde willekeurige variabele een waarde aanneemt binnen een bepaald bereik.

Op een TI-83- of TI-84-rekenmachine gebruikt deze functie de volgende syntaxis

normalcdf (onder, boven, μ, σ)

Goud:

• lager = lagere waarde van het bereik
• bovenste = bovenste waarde van het bereik
• μ = populatiegemiddelde
• σ = standaarddeviatie van de populatie

Stel bijvoorbeeld dat een willekeurige variabele normaal verdeeld is met een gemiddelde van 50 en een standaarddeviatie van 4. De waarschijnlijkheid dat een willekeurige variabele een waarde tussen 48 en 52 aanneemt, kan als volgt worden berekend:

normaalcdf(48, 52, 50, 4) = 0,3829

We kunnen dit antwoord in Excel reproduceren met behulp van de functie NORM.DIST() , die de volgende syntaxis gebruikt:

NORM.VERD(x, σ, μ, cumulatief)

Goud:

• x = individuele gegevenswaarde
• μ = populatiegemiddelde
• σ = standaarddeviatie van de populatie
• cumulatief = FALSE bereken PDF; WAAR berekent de CDF

De volgende voorbeelden laten zien hoe u deze functie in de praktijk kunt gebruiken.

Voorbeeld 1: Waarschijnlijkheid tussen twee waarden

Stel dat een willekeurige variabele normaal verdeeld is met een gemiddelde van 50 en een standaarddeviatie van 4. De kans dat een willekeurige variabele een waarde tussen 48 en 52 aanneemt, kan als volgt worden berekend:

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

De volgende afbeelding laat zien hoe u deze berekening in Excel uitvoert:

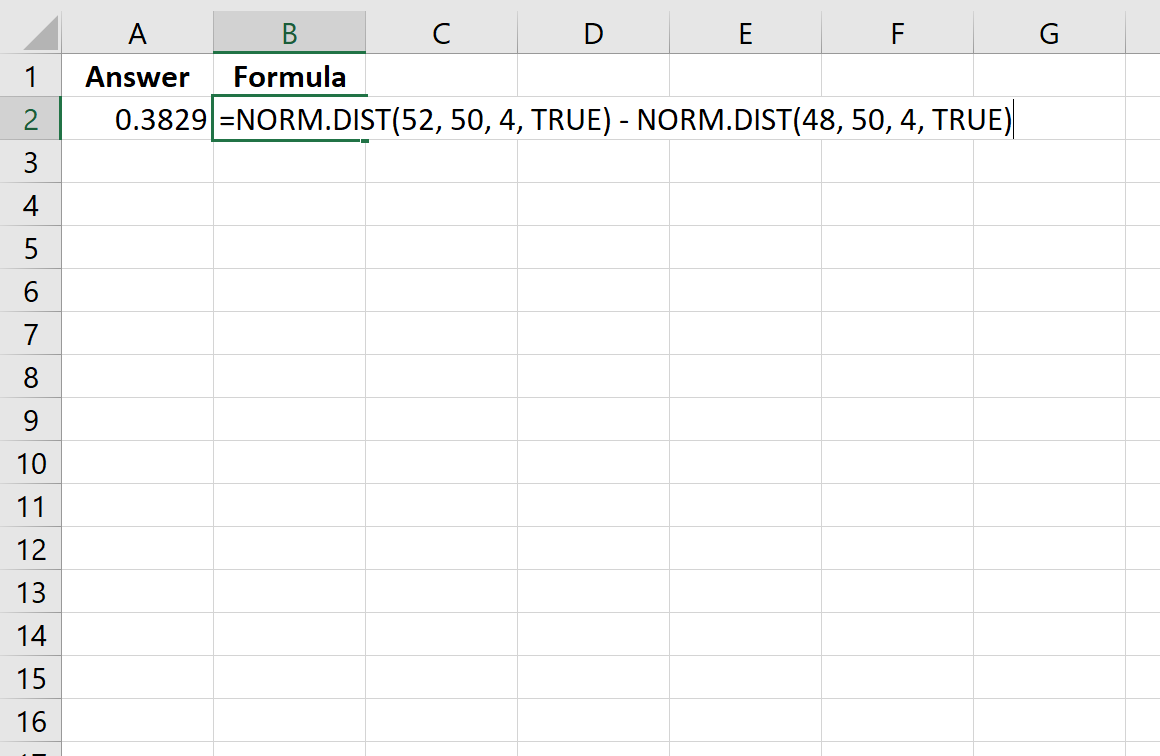
De waarschijnlijkheid blijkt 0,3829 te zijn.

Voorbeeld 2: Waarschijnlijkheid kleiner dan één waarde

Stel dat een willekeurige variabele normaal verdeeld is met een gemiddelde van 50 en een standaarddeviatie van 4. De kans dat een willekeurige variabele een waarde kleiner dan 48 aanneemt, kan als volgt worden berekend:

 =NORM. DIST (48, 50, 4, TRUE )

De volgende afbeelding laat zien hoe u deze berekening in Excel uitvoert:

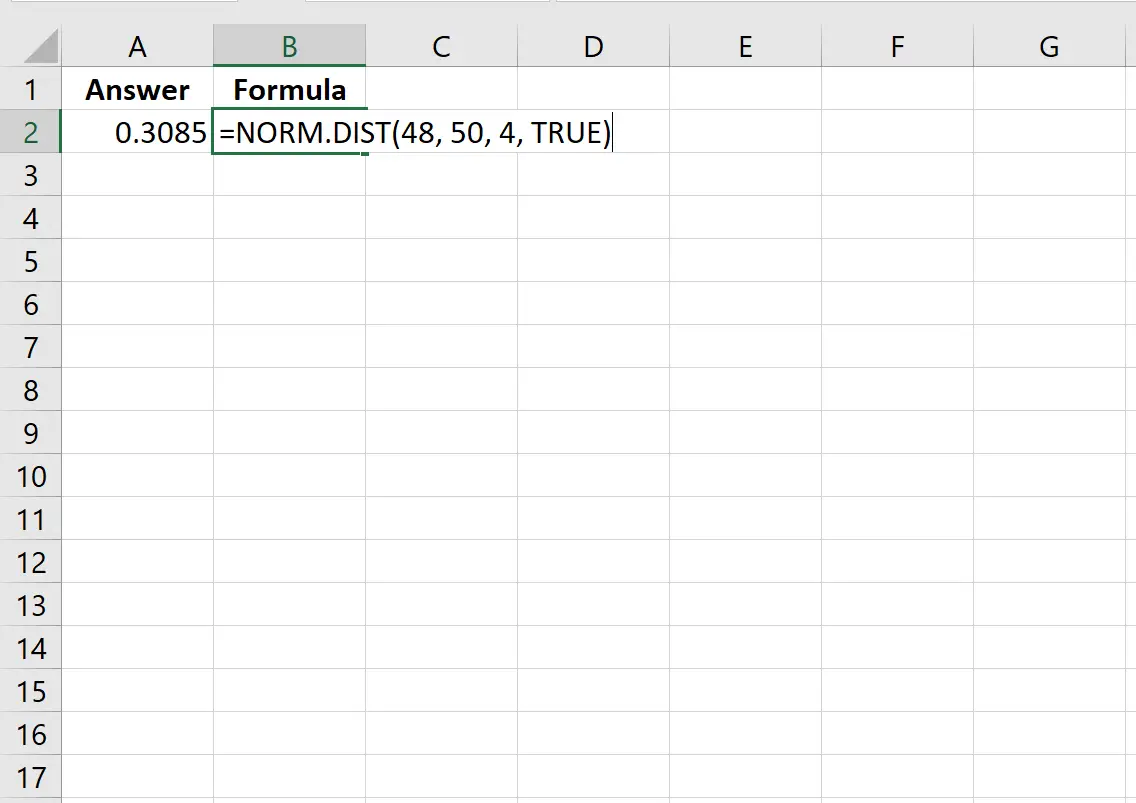
De waarschijnlijkheid blijkt 0,3085 te zijn.

Voorbeeld 3: Waarschijnlijkheid groter dan een waarde

Stel dat een willekeurige variabele normaal verdeeld is met een gemiddelde van 50 en een standaarddeviatie van 4. De kans dat een willekeurige variabele een waarde groter dan 55 aanneemt, kan als volgt worden berekend:

 =1 - NORM. DIST (55, 50, 4, TRUE )

De volgende afbeelding laat zien hoe u deze berekening in Excel uitvoert:

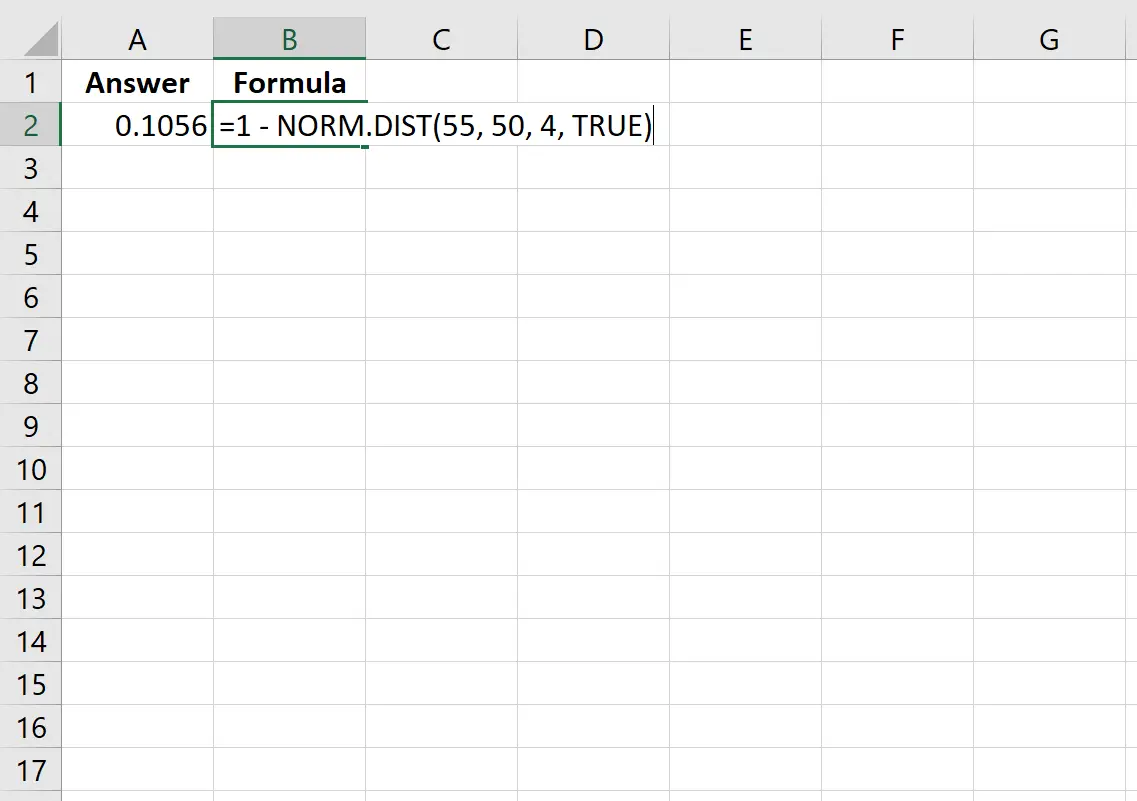
De waarschijnlijkheid blijkt 0,1056 te zijn.

Aanvullende bronnen

U kunt deze normale CDF-calculator ook gebruiken om automatisch de kansen te vinden die bij een normale verdeling horen.