Standaard normale verdeling

In dit artikel wordt uitgelegd wat de standaardnormale verdeling is en waarvoor deze wordt gebruikt. Ook vind je de eigenschappen van de standaardnormale verdeling, de tabel met zijn karakteristieke waarden en daarnaast een opgeloste oefening.

Wat is de standaardnormale verdeling?

De standaardnormale verdeling , ook wel de eenheidsnormale verdeling genoemd, is het eenvoudigste geval van een normale verdeling. Nauwkeuriger gezegd, de standaardnormale verdeling is een normale verdeling met gemiddelde en standaardafwijkingswaarden gelijk aan respectievelijk 0 en 1.

Daarom wordt de standaardnormale verdeling gedefinieerd als N(0,1), waarbij de eerste parameter het gemiddelde van de verdeling is en de tweede parameter de standaardafwijking (of SD).

De grafiek van de standaardnormale verdeling is daarom als volgt:

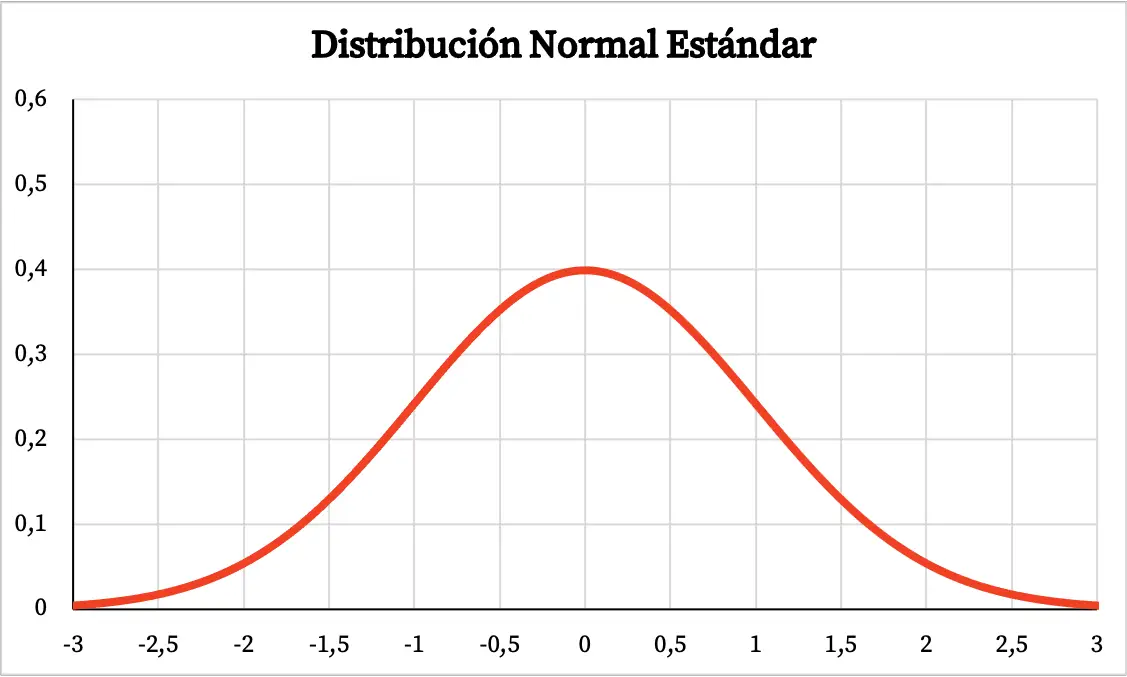
Formule voor de standaardnormale verdeling

Om een normale verdeling om te zetten in een standaardnormale verdeling, moet je het gemiddelde van de normale verdeling aftrekken van al zijn waarden en vervolgens delen door de standaardafwijking van de normale verdeling.

De formule voor de standaardnormale verdeling is daarom als volgt:

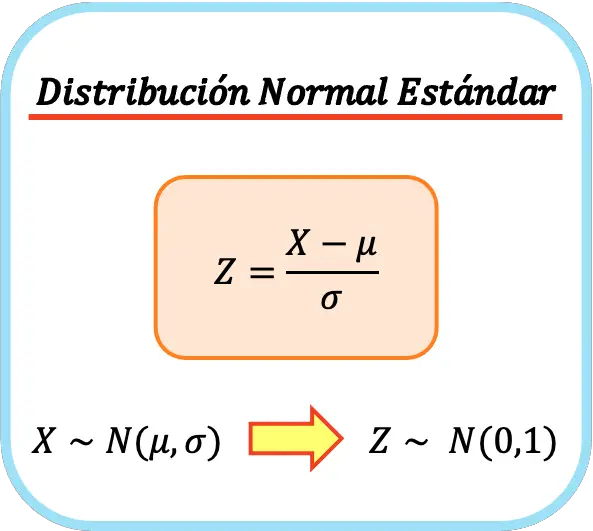
Op deze manier zullen het rekenkundig gemiddelde en de standaarddeviatie van de nieuwe variabele respectievelijk 0 en 1 zijn, zodat we een standaardnormale verdeling verkrijgen. Dit proces wordt ook wel univariate normalisatie of univariate normalisatie genoemd.

Standaard normale verdelingstabel

De tabel van een standaardnormale verdeling is een tabel die de kansen bevat dat een waargenomen waarde kleiner is dan een gegeven waarde van de standaardnormale verdeling.

Omdat de functie van een normale verdeling afhangt van het gemiddelde en de standaarddeviatie, wordt bovendien de standaardnormale verdelingstabel bij uitbreiding ook gebruikt om de waarschijnlijkheden van een normale verdeling te bepalen. Om dit te doen, wordt de normale verdeling in een standaardnormale verdeling getypt en vervolgens kijken we in de tabel welke waarschijnlijkheid daarmee overeenkomt.

De waarden in de standaard normale verdelingstabel zijn dus als volgt:

Voorbeeld van standaardnormale verdeling

Nu we de definitie van standaardnormale verdeling kennen en wat de formule ervan is, volgt hieronder een concreet voorbeeld om het concept goed te begrijpen.

• Een continue willekeurige variabele volgt een normale verdeling met een gemiddelde van 45 en een standaarddeviatie van 15. Wat is de kans op het verkrijgen van een waarde kleiner dan of gelijk aan 58?

Om de waarschijnlijkheid van een normale verdeling te vinden, moeten we de kenmerkentabel ervan gebruiken, maar om dat te doen moeten we eerst het typeproces uitvoeren om de standaard normale verdeling te krijgen. We gebruiken daarom de standaardnormaalverdelingsformule:

Dus trekken we het gemiddelde af van de waarschijnlijkheidswaarde en delen we dit door de standaarddeviatie

Nadat we de variabele hebben gestandaardiseerd, gaan we naar de standaardwaarschijnlijkheidstabel voor normale verdeling (zie hierboven) om te zien met welke waarschijnlijkheid de waarde van 0,87 overeenkomt:

De kans op het verkrijgen van een waarde gelijk aan of kleiner dan 58 is daarom 80,78%.

Kenmerken van de standaardnormale verdeling

De standaardnormale verdeling heeft de volgende kenmerken:

• De standaardnormale verdeling is een symmetrische verdeling, gecentreerd op 0.
• Net als bij een normale verdeling is de standaard normale verdelingsgrafiek klokvormig, waarbij het grootste deel van het grafiekgebied rond het gemiddelde valt.
• Daarom hebben het gemiddelde, de modus en de mediaan van een normale verdeling dezelfde waarde, namelijk 0.
• De standaardnormale verdeling heeft een maximum bij z=0.
• Op dezelfde manier heeft de standaardnormale verdeling twee buigpunten, op z=-1 en z=+1.
• Volgens de vuistregel weten we dat 68% van de waarden in een standaard normale verdeling tussen +1 en -1 valt, 95% van de waarden tussen +2 en -2 en 99,7% van de waarden tussen + 3 en – 3.