Normale verdeling

Von Dr.benjamin anderson August 3, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat de normale verdeling in de statistiek is. U vindt dus de definitie van normale verdeling, voorbeelden van normale verdelingen en wat de eigenschappen van normale verdeling zijn.

Wat is de normale verdeling?

De normale verdeling is een continue kansverdeling waarvan de grafiek klokvormig is en symmetrisch ten opzichte van het gemiddelde. In de statistiek wordt de normale verdeling gebruikt om verschijnselen met zeer verschillende kenmerken te modelleren. Daarom is deze verdeling zo belangrijk.

In feite wordt de normale verdeling in de statistiek beschouwd als verreweg de belangrijkste verdeling van alle waarschijnlijkheidsverdelingen, omdat deze niet alleen een groot aantal verschijnselen uit de echte wereld kan modelleren, maar de normale verdeling ook kan worden gebruikt om andere typen kansverdelingen te benaderen. distributies. onder bepaalde omstandigheden.

Het symbool voor normale verdeling is de hoofdletter N. Om aan te geven dat een variabele een normale verdeling volgt, wordt deze aangegeven met de letter N en worden de waarden van het rekenkundig gemiddelde en de standaarddeviatie tussen haakjes toegevoegd.

$X\sim N(\mu,\sigma)$

De normale verdeling heeft veel verschillende namen, waaronder Gaussische verdeling , Gaussische verdeling en Laplace-Gauss-verdeling .

Voorbeelden van normale verdelingen

Datasets die een normale verdeling volgen, bevatten doorgaans een groot aantal observaties en bestrijken zeer algemene onderwerpen. Hieronder staan enkele voorbeelden van statistische steekproeven die over het algemeen met een normale verdeling kunnen worden gemodelleerd.

Voorbeelden van normale verdeling:

De grootte van de studenten in een cursus.
Het IQ van de werknemers van een bedrijf.
Het aantal defecte onderdelen dat per dag in een fabriek wordt geproduceerd.
De cijfers die studenten van een cursus op een examen behalen.
De winstgevendheid van aandelen van beursgenoteerde bedrijven.

Normale verdelingsgrafiek

Als we eenmaal hebben gezien wat de normale verdeling is en enkele voorbeelden van dit type kansverdeling hebben gezien, gaan we kijken hoe de grafiek eruit ziet om het concept beter te begrijpen.

In de volgende grafiek kunt u zien hoe de dichtheidsfunctie van de normale verdeling varieert, afhankelijk van de waarden van het rekenkundig gemiddelde en de standaarddeviatie.

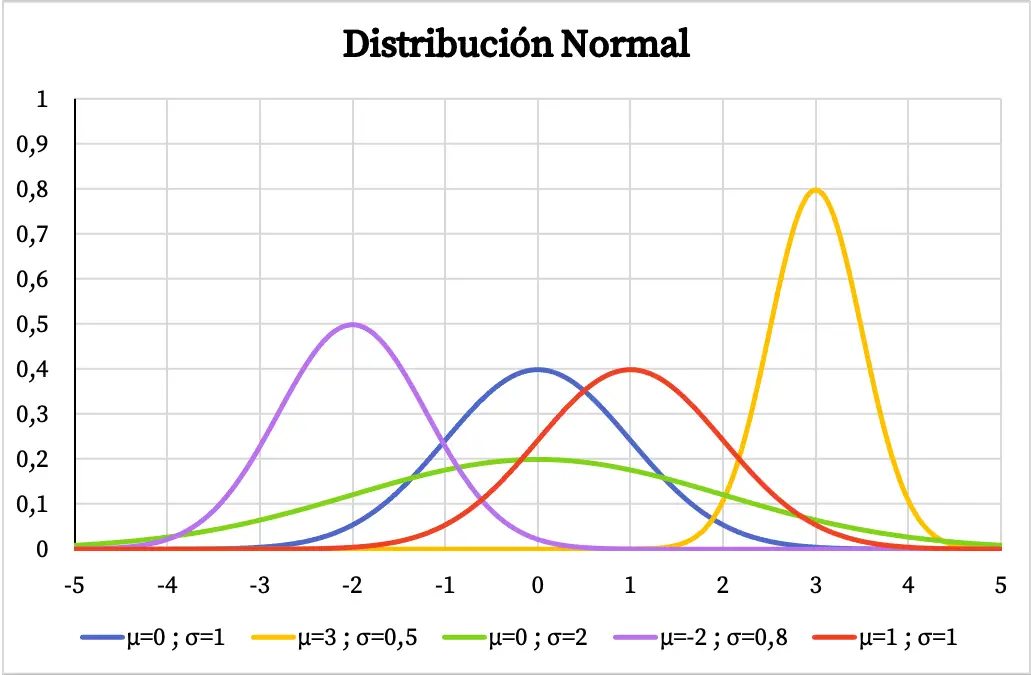
Als een variabele een klokvorm heeft gecentreerd op het rekenkundig gemiddelde, betekent dit dat de meest herhaalde waarde het gemiddelde is en dat waarden rond het gemiddelde vaker worden herhaald dan extreme waarden. Op dezelfde manier geldt: hoe groter de standaardafwijking van de normale verdeling, hoe vlakker de vorm van de grafische weergave.

Aan de andere kant hangt de grafiek van de cumulatieve waarschijnlijkheidsfunctie van de normale verdeling ook af van de waarden van het rekenkundig gemiddelde en de standaarddeviatie, zoals je kunt zien in de volgende afbeelding:

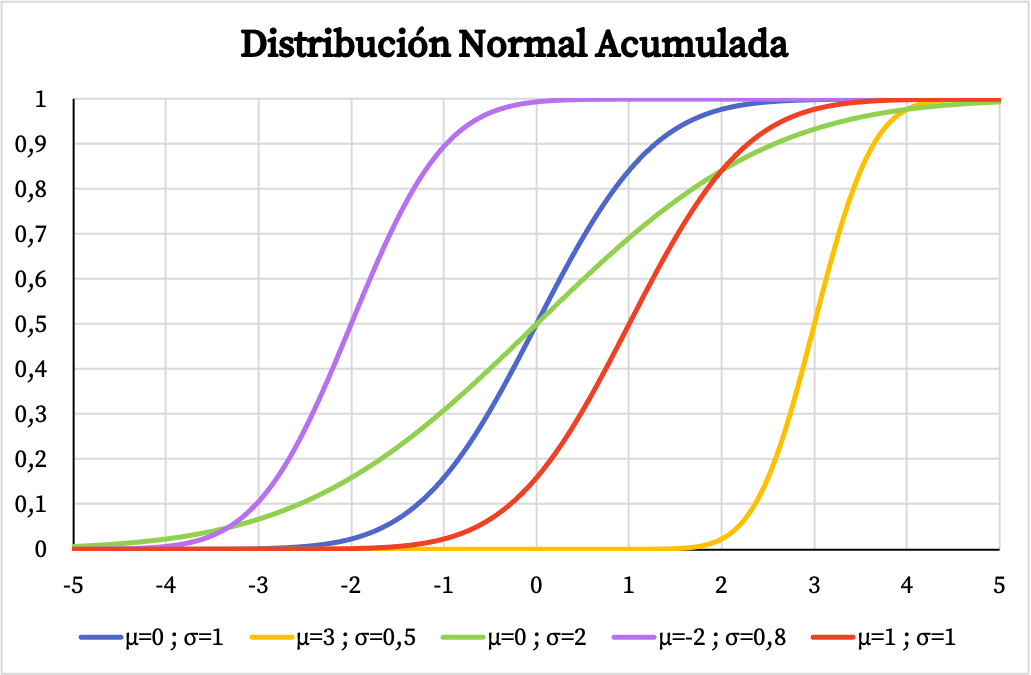
De dichtheidsfunctie en de verdelingsfunctie van de normale verdeling maken het mogelijk om kansen te berekenen die verband houden met deze verdeling. In plaats van hun formules te gebruiken, kunt u echter rechtstreeks de normale verdelingstabellen gebruiken, omdat dit sneller is. U kunt deze tabellen raadplegen via de volgende link:

➤ Zie: Normale verdelingstabel

Kenmerken van de normale verdeling

De normale verdeling heeft de volgende kenmerken:

De normale verdeling hangt af van twee karakteristieke parameters, namelijk het rekenkundig gemiddelde (μ) en de standaardafwijking (σ).

$X\sim N(\mu,\sigma)$

De normale verdeling kan positieve en negatieve waarden aannemen, dus het domein van de normale verdeling bestaat uit reële getallen.

$x\in \mathbb{R}$

De mediaan en modus van de normale verdeling zijn gelijk aan het rekenkundig gemiddelde van de verdeling.

$Me=Mo=\mu$

De scheefheidscoëfficiënt en de kurtosis-coëfficiënt van de normale verdeling zijn nul.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

De formule voor de dichtheidsfunctie van de normale verdeling is:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Op dezelfde manier is de formule voor de cumulatieve waarschijnlijkheidsfunctie van de normale verdeling:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Een toepassing van de centrale limietstelling is dat een Poisson-verdeling een normale verdeling kan benaderen wanneer de waarde van λ voldoende groot is.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Een andere toepassing van de centrale limietstelling is dat een binominale verdeling kan worden benaderd door een normale verdeling voor datasets met een groot aantal waarnemingen.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Standaard normale verdeling

De standaardnormale verdeling , ook wel de eenheidsnormale verdeling genoemd, is het eenvoudigste geval van een normale verdeling. Nauwkeuriger gezegd, de standaardnormale verdeling is een normale verdeling met gemiddelde en standaardafwijkingswaarden gelijk aan respectievelijk 0 en 1.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Merk op dat elke normale verdeling kan worden omgezet in een standaardnormale verdeling door een proces toe te passen dat typen wordt genoemd, waarbij het rekenkundig gemiddelde van elke waarde wordt afgetrokken en vervolgens wordt gedeeld door de standaarddeviatie.

Bovendien wordt de standaardnormale verdeling gebruikt om de waarschijnlijkheid van een normale verdeling te bepalen met behulp van de waarschijnlijkheidstabel. Om dus een waarschijnlijkheid van een normale verdeling te vinden, wordt de variabele eerst ingevoerd om deze om te zetten in een standaard normale verdeling en vervolgens kijken we in de tabel om te zien wat de overeenkomstige waarschijnlijkheidswaarde is. Wilt u meer weten, klik dan op de volgende link:

➤ Zie: Standaardnormale verdeling

De normale verdeling en de empirische regel

In de statistiek is de vuistregel , ook wel de 68-95-99.7-regel genoemd, een regel die het percentage waarden in een normale verdeling definieert dat binnen drie standaarddeviaties van het gemiddelde valt.

Meer specifiek luidt de vuistregel het volgende:

68% van de waarden in een normale verdeling liggen binnen één standaarddeviatie van het gemiddelde.
95% van de waarden in een normale verdeling liggen binnen twee standaarddeviaties van het gemiddelde.
99,7% van de waarden in een normale verdeling vallen binnen drie standaarddeviaties van het gemiddelde.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder