Normale verdeling en standaardnormale verdeling: het verschil

De normale verdeling is de meest gebruikte kansverdeling in de statistiek.

Het heeft de volgende eigenschappen:

• Symmetrisch
• Klokvormig
• Het gemiddelde en de mediaan zijn gelijk; beide gelegen in het centrum van de distributie

Het gemiddelde van de normale verdeling bepaalt de locatie en de standaardafwijking bepaalt de spreiding.

De volgende grafiek toont bijvoorbeeld drie normale verdelingen met verschillende gemiddelden en standaarddeviaties:

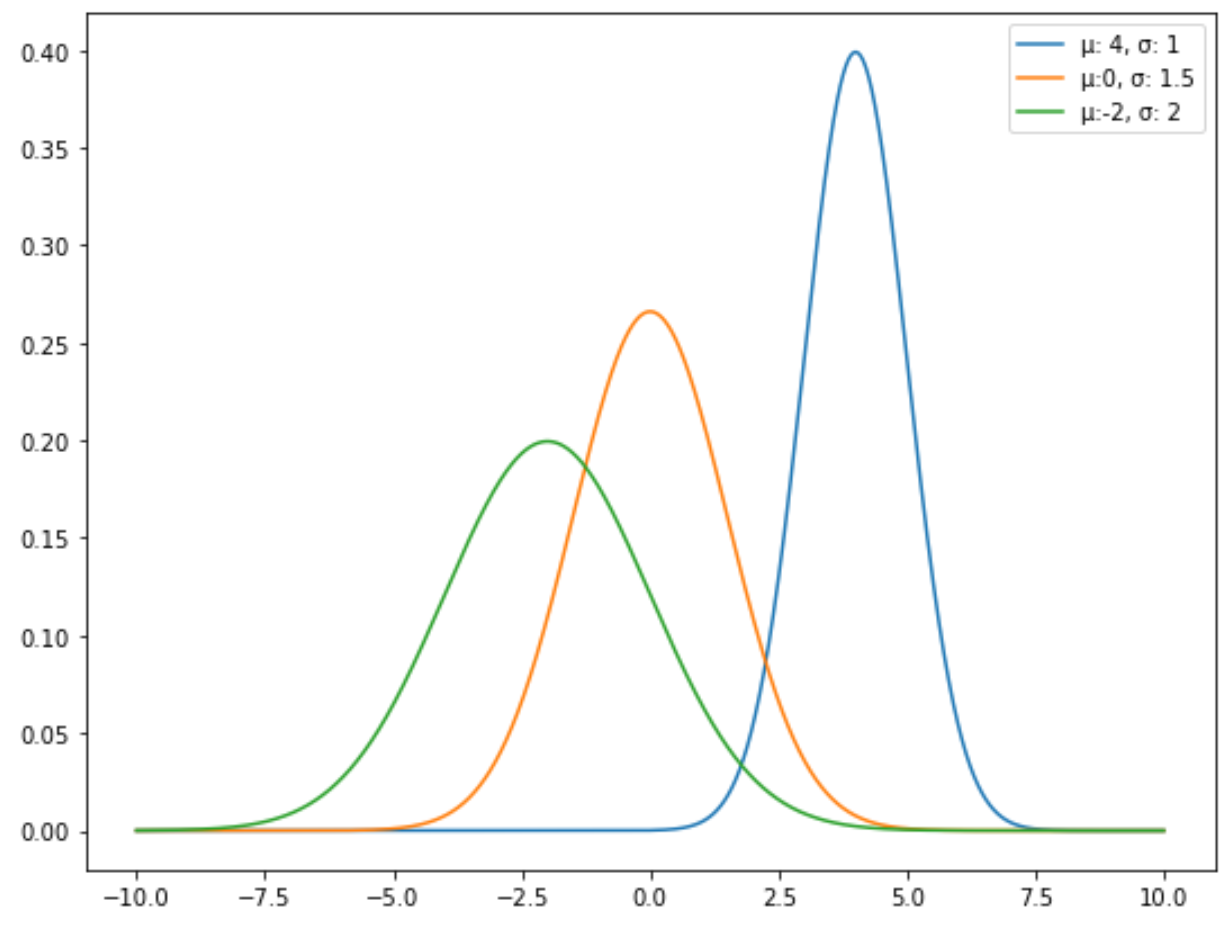
De standaardnormale verdeling is een specifiek type normale verdeling waarbij het gemiddelde 0 is en de standaarddeviatie 1.

De volgende grafiek toont een standaardnormale verdeling:

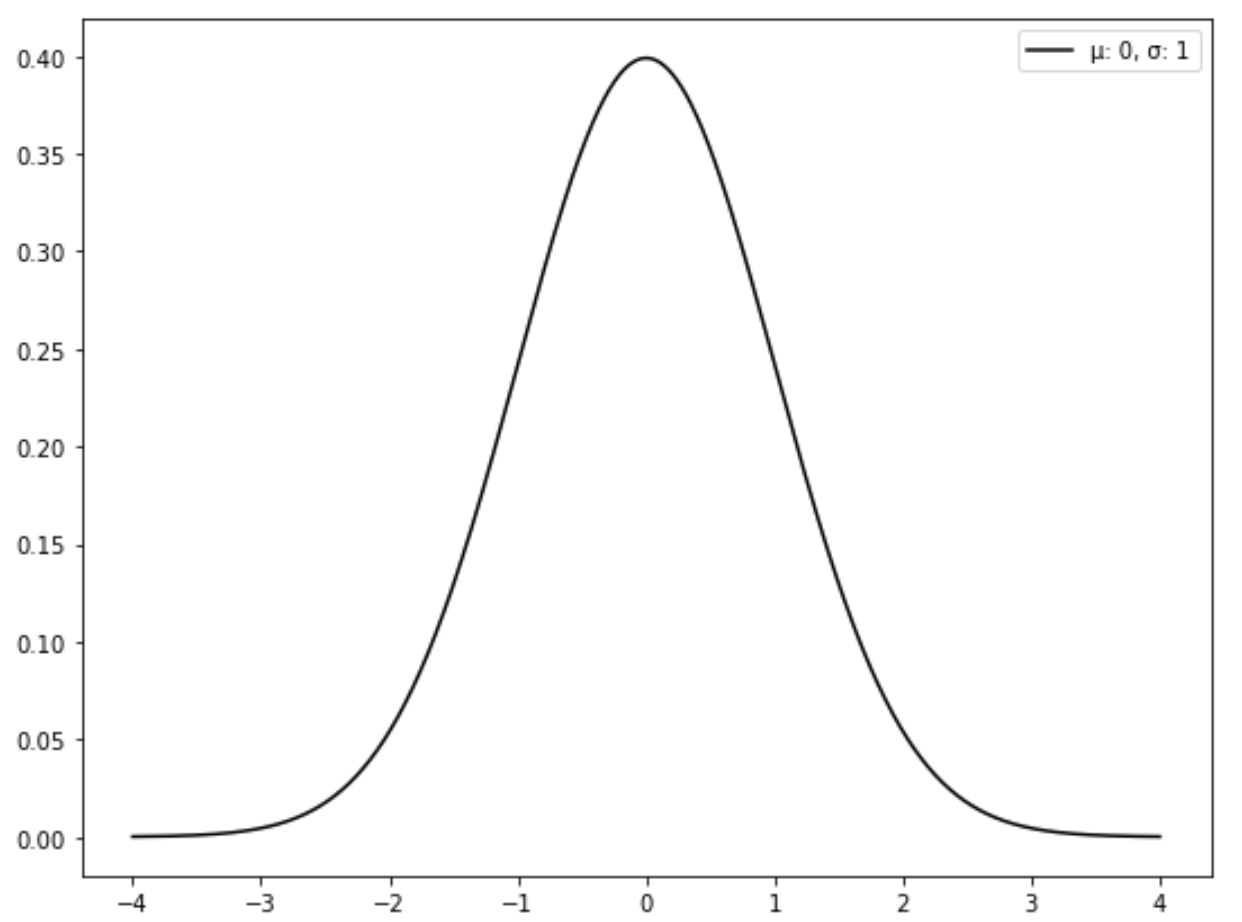
Hoe een normale verdeling naar een standaardnormale verdeling te converteren

Elke normale verdeling kan worden geconverteerd naar een standaard normale verdeling door de gegevenswaarden om te zetten naar z-scores, met behulp van de volgende formule:

z = (x – μ) / σ

Goud:

• x: waarde van individuele gegevens
• μ: gemiddelde van de verdeling
• σ: Standaardafwijking van de verdeling

Stel dat we bijvoorbeeld de volgende gegevensset hebben met een gemiddelde van 6 en een standaardafwijking van 2,152:

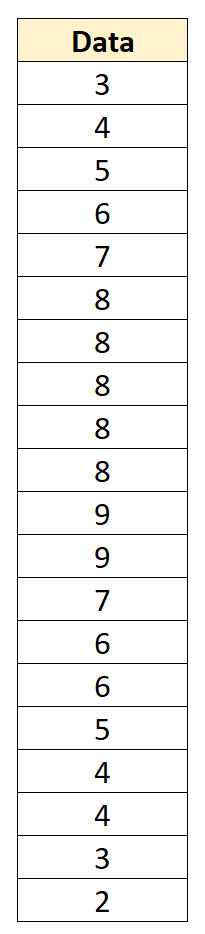
We kunnen elke individuele gegevenswaarde omzetten in een z-score door van elke waarde 6 af te trekken en te delen door 2,152:

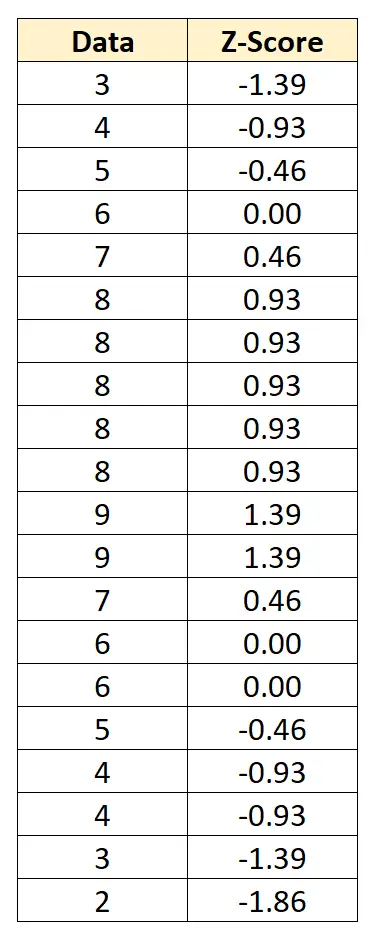
De z-score vertelt ons hoeveel standaardafwijkingen elk gegevenspunt van het gemiddelde verwijderd is. De eerste gegevenswaarde „3“ ligt bijvoorbeeld 1,39 standaardafwijkingen onder het gemiddelde.

Het gemiddelde van deze verdeling van scores heeft een gemiddelde van nul en een standaarddeviatie van één.

Hoe de standaardnormale verdeling te gebruiken

Een standaardnormale verdeling heeft de volgende eigenschappen:

• Ongeveer 68% van de gegevens valt binnen één standaarddeviatie van het gemiddelde
• Ongeveer 95% van de gegevens valt binnen twee standaarddeviaties van het gemiddelde.
• Ongeveer 99,7% van de gegevens valt binnen drie standaarddeviaties van het gemiddelde.

Dit staat bekend als een vuistregel en wordt gebruikt om de verdeling van waarden in een dataset te begrijpen.

Stel bijvoorbeeld dat de hoogte van planten in een bepaalde tuin normaal verdeeld is met een gemiddelde van 47,4 inch en een standaardafwijking van 2,4 inch.

Welk percentage planten is volgens de vuistregel minder dan 54,6 centimeter lang?

De vuistregel stelt dat voor een gegeven dataset met een normale verdeling 99,7% van de datawaarden binnen drie standaarddeviaties van het gemiddelde vallen. Dit betekent dat 49,85% van de waarden tussen het gemiddelde en drie standaarddeviaties boven het gemiddelde liggen.

In dit voorbeeld is 54,6 drie standaarddeviaties boven het gemiddelde. Omdat we weten dat 50% van de gegevenswaarden kleiner is dan het gemiddelde in een normale verdeling, is een totaal van 50% + 49,85% = 99,85% van de waarden minder dan 54,6.

Dus 99,85% van de planten is minder dan 150 cm hoog.

Aanvullende bronnen

Problemen bij het oefenen van vuistregels
Rekenmachine met vuistregels
Hoe u de vuistregel toepast in Excel