Normale verdeling en t-verdeling: wat is het verschil?

Denormale verdeling is de meest gebruikte verdeling in alle statistieken en staat bekend als symmetrisch en klokvormig.

Een nauw verwante verdeling is de t-verdeling , die ook symmetrisch en klokvormig is, maar zwaardere „staarten“ heeft dan de normale verdeling.

Met andere woorden: er bevinden zich meer waarden in de verdeling aan de uiteinden dan in het midden vergeleken met de normale verdeling:

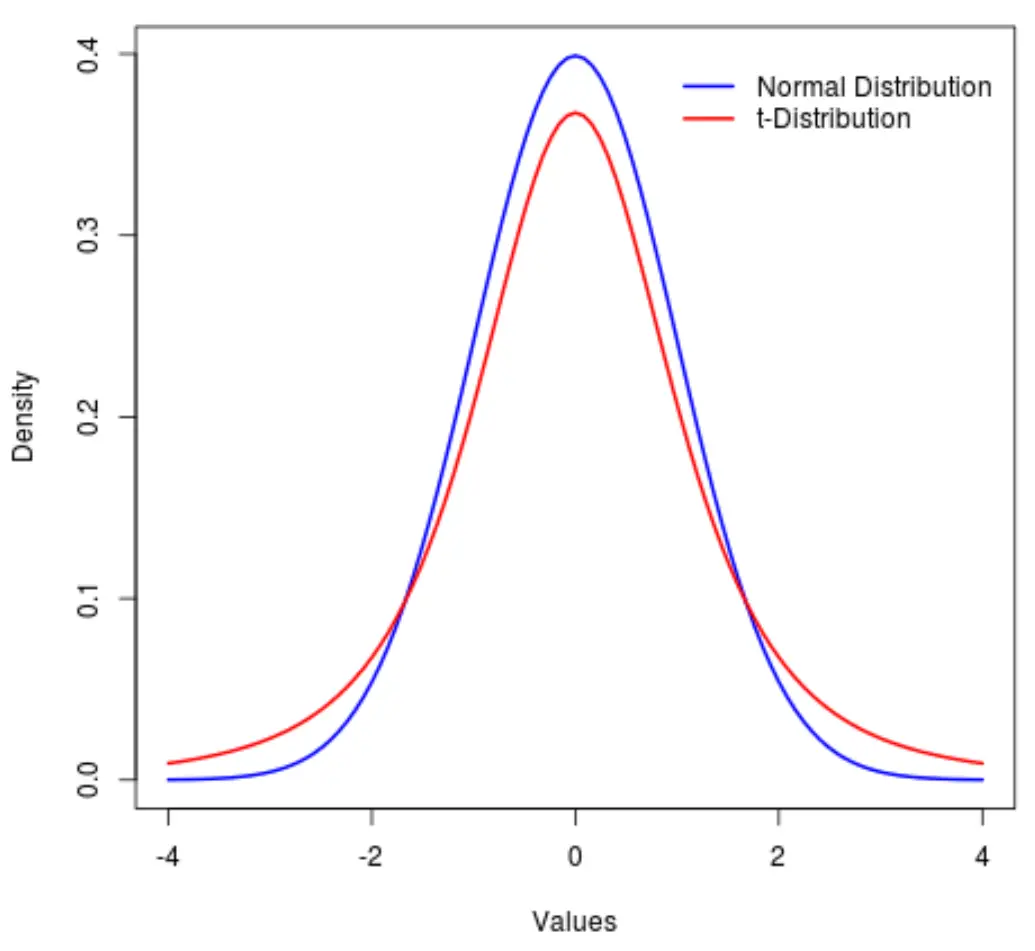
In statistisch jargon gebruiken we een metriek genaamd kurtosis om te meten hoe ‘zwaar’ een verdeling is. We zouden dus zeggen dat de kurtosis van een t-verdeling groter is dan die van een normale verdeling.

In de praktijk gebruiken we de t-verdeling meestal bij het testen van hypothesen of het construeren van betrouwbaarheidsintervallen .

De formule voor het berekenen van een betrouwbaarheidsinterval voor een populatiegemiddelde is bijvoorbeeld:

Betrouwbaarheidsinterval = x +/- t _{1-α/2, n-1} *(s/√ n )

Goud:

• x : steekproefgemiddelden
• t: de kritische t-waarde, gebaseerd op het significantieniveau α en de steekproefomvang n
• s: standaardafwijking van het monster
• n: steekproefomvang

In deze formule gebruiken we de kritische waarde van tabel t in plaats van de kritische waarde van tabel z wanneer een van de volgende voorwaarden waar is:

• We kennen de standaarddeviatie van de populatie niet.
• De steekproefomvang is kleiner dan of gelijk aan 30.

Het volgende stroomdiagram biedt een handige manier om te weten of u de kritische waarde uit tabel t of tabel z moet gebruiken:

Het belangrijkste verschil tussen het gebruik van de t-verdeling en het gebruik van de normale verdeling bij het construeren van betrouwbaarheidsintervallen is dat de kritische waarden van de t-verdeling groter zullen zijn, wat leidt tot bredere betrouwbaarheidsintervallen.

Stel dat we bijvoorbeeld een betrouwbaarheidsinterval van 95% willen construeren voor het gemiddelde gewicht van een populatie schildpadden, om zo een willekeurige steekproef van schildpadden te verzamelen met de volgende informatie:

• Steekproefomvang n = 25
• Gemiddeld monstergewicht x = 300
• Steekproefstandaardafwijking s = 18,5

De kritische z-waarde voor een betrouwbaarheidsniveau van 95% is 1,96 , terwijl een kritische t-waarde voor een betrouwbaarheidsinterval van 95% met df = 25-1 = 24 vrijheidsgraden 2,0639 is.

Een betrouwbaarheidsinterval van 95% voor het populatiegemiddelde met behulp van een z-kritische waarde is dus:

95% BI = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Terwijl een betrouwbaarheidsinterval van 95% voor het populatiegemiddelde bij gebruik van een t-kritische waarde is:

95% BI = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Merk op dat het betrouwbaarheidsinterval met de t-kritische waarde groter is.

Het idee hier is dat als we een kleine steekproefomvang hebben, we minder zeker zijn van het werkelijke populatiegemiddelde. Het is dus nuttig om de t-verdeling te gebruiken om bredere betrouwbaarheidsintervallen te produceren die een grotere kans hebben om het werkelijke populatiegemiddelde te bevatten.

Visualisatie van de vrijheidsgraden voor de t-verdeling

Opgemerkt moet worden dat naarmate de vrijheidsgraden toenemen, de t-verdeling de normale verdeling benadert.

Om dit te illustreren, bekijken we de volgende grafiek, die de vorm van de t-verdeling toont met de volgende vrijheidsgraden:

• df = 3
• df = 10
• df = 30

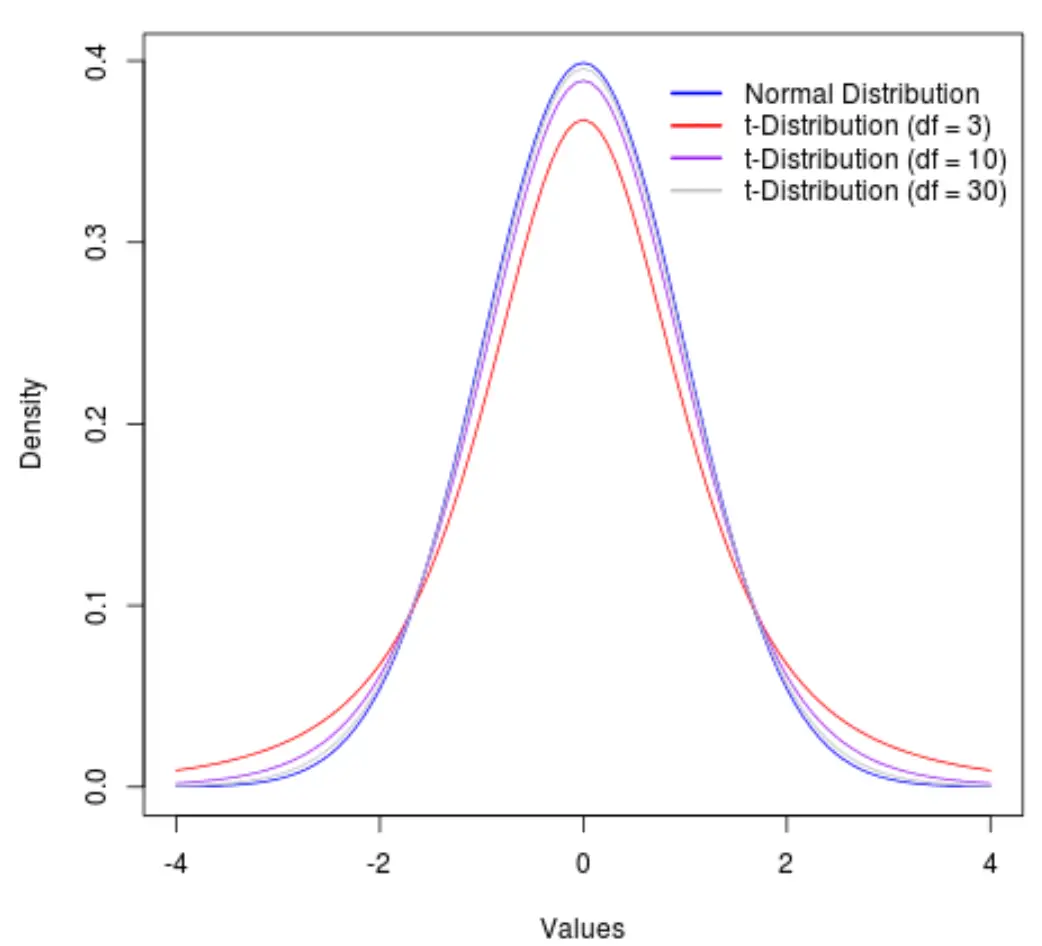
Boven de 30 vrijheidsgraden worden de t-verdeling en de normale verdeling zo vergelijkbaar dat de verschillen tussen het gebruik van een t-kritische waarde en een z-kritische waarde in de formules verwaarloosbaar worden.