Normale of uniforme verdeling: wat is het verschil?

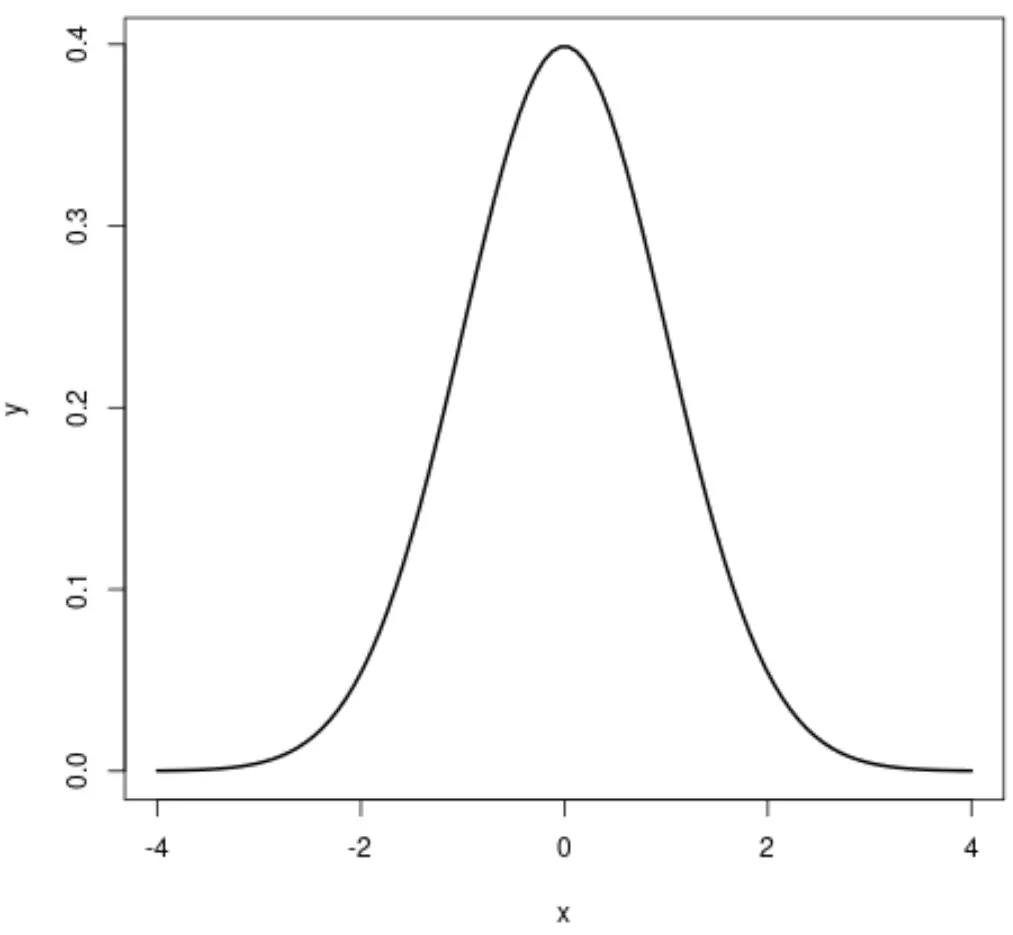
De normale verdeling is de meest gebruikte kansverdeling in de statistiek.

Het heeft de volgende eigenschappen:

• Symmetrisch
• Klokvormig

Als we een grafiek van de normale verdeling maken, ziet deze er als volgt uit:

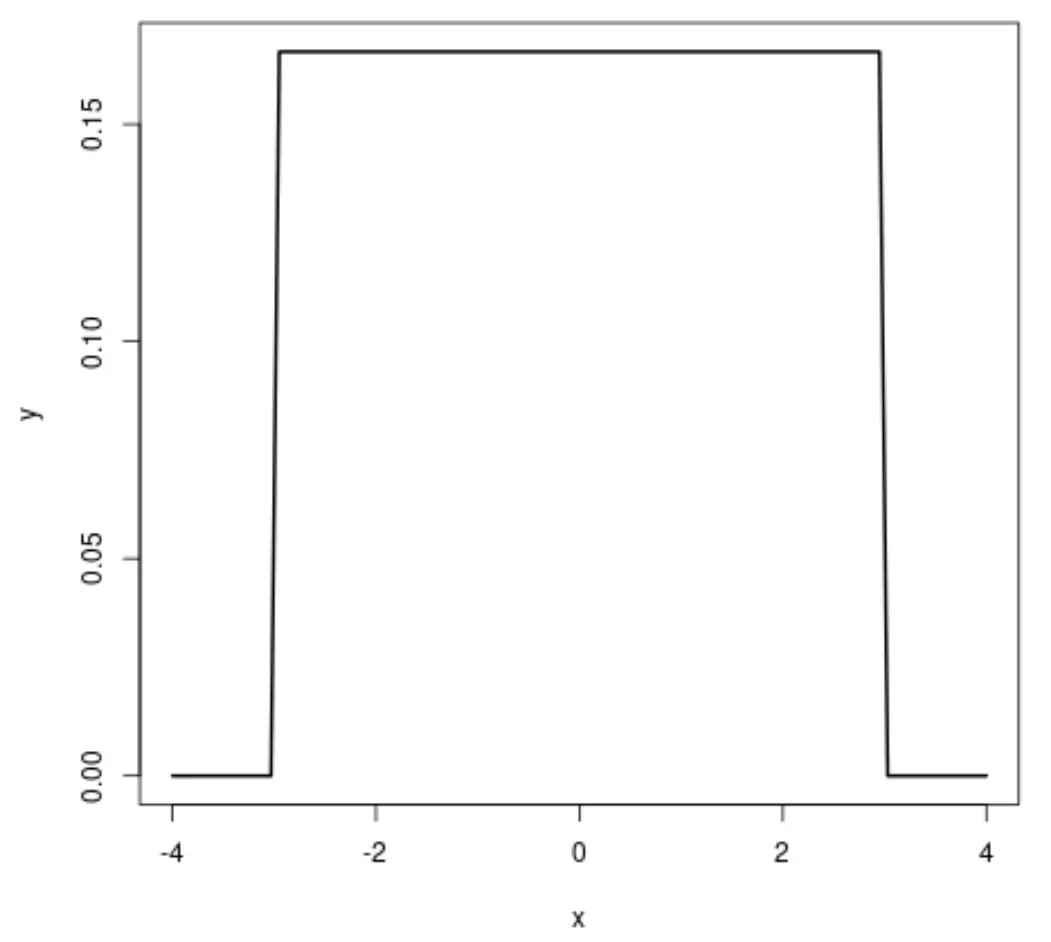
De uniforme verdeling is een kansverdeling waarbij elke waarde tussen een interval van a tot en met b dezelfde kans heeft om te voorkomen.

Het heeft de volgende eigenschappen:

• Symmetrisch
• Rechthoekig van vorm

Als we een grafiek van de uniforme verdeling maken, ziet deze er als volgt uit:

De normale verdeling en de uniforme verdeling delen de volgende gelijkenis :

• De twee verdelingen zijn symmetrisch. Dat wil zeggen, als we een lijn door het midden van de verdeling zouden trekken, zouden de linker- en rechterkant van de verdeling elkaar perfect weerspiegelen:

De twee distributies hebben echter het volgende verschil :

• De verdelingen hebben verschillende vormen.
• De normale verdeling is klokvormig, wat betekent dat waarden nabij het midden van de verdeling vaker voorkomen dan waarden aan de staarten van de verdeling.
• De uniforme verdeling is rechthoekig van vorm, wat betekent dat elke waarde in de verdeling dezelfde waarschijnlijkheid heeft om te voorkomen.

Normale distributie of uniforme distributie: wanneer gebruik je ze?

De normale verdeling wordt gebruikt om verschijnselen te modelleren die de neiging hebben de vorm van een „belcurve“ te volgen. Het is bijvoorbeeld goed gedocumenteerd dat het geboortegewicht van pasgeborenen normaal gesproken gemiddeld rond de 7,5 pond ligt.

Het histogram van het geboortegewicht van pasgeborenen in de Verenigde Staten vertoont een belvorm die over het algemeen overeenkomt met de normale verdeling:

De meeste baby’s wegen waarschijnlijk ongeveer 7,5 pond, waarbij een paar minder dan 7 pond wegen en een paar meer dan 8 pond wegen.

Omgekeerd wordt de uniforme verdeling gebruikt om scenario’s te modelleren waarin elke potentiële uitkomst even waarschijnlijk is.

Een klassiek voorbeeld is het gooien van een dobbelsteen. Als je één keer een dobbelsteen gooit, volgt de kans dat deze op een getal tussen 1 en 6 valt een uniforme verdeling, omdat elk getal dezelfde kans heeft om te verschijnen.

Er zijn bijvoorbeeld zes mogelijke getallen waarop de dobbelsteen kan landen, dus de kans dat je een 1 gooit is 1/6.

Op dezelfde manier is de kans dat je een 2 gooit 1/6.

Op dezelfde manier is de kans dat u een 3 gooit 1/6.

Enzovoort.

Bonus: hoe u de normale en uniforme verdeling in kaart brengt

We hebben de volgende code in R gebruikt om grafieken van de normale en uniforme verdelingen te maken:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

Aanvullende bronnen

6 concrete voorbeelden van de normale verdeling
5 concrete voorbeelden van uniforme distributie
Symmetrische verdeling: definitie + voorbeelden