Hoe te testen op normaliteit in r (4 methoden)

Veel statistische tests gaan ervan uit dat datasets normaal verdeeld zijn.

Er zijn vier gebruikelijke manieren om deze aanname in R te controleren:

1. (Visuele methode) Maak een histogram.

• Als het histogram ongeveer de vorm van een klok heeft, wordt aangenomen dat de gegevens normaal verdeeld zijn.

2. (Visuele methode) Maak een QQ-plot.

• Als de punten op de grafiek grofweg langs een rechte diagonale lijn liggen, wordt aangenomen dat de gegevens normaal verdeeld zijn.

3. (Formele statistische test) Voer een Shapiro-Wilk-test uit.

• Als de p-waarde van de test groter is dan α = 0,05, wordt aangenomen dat de gegevens normaal verdeeld zijn.

4. (Formele statistische test) Voer een Kolmogorov-Smirnov-test uit.

• Als de p-waarde van de test groter is dan α = 0,05, wordt aangenomen dat de gegevens normaal verdeeld zijn.

De volgende voorbeelden laten zien hoe u elk van deze methoden in de praktijk kunt gebruiken.

Methode 1: Maak een histogram

De volgende code laat zien hoe u een histogram maakt voor een normaal verdeelde en niet-normaal verdeelde gegevensset in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

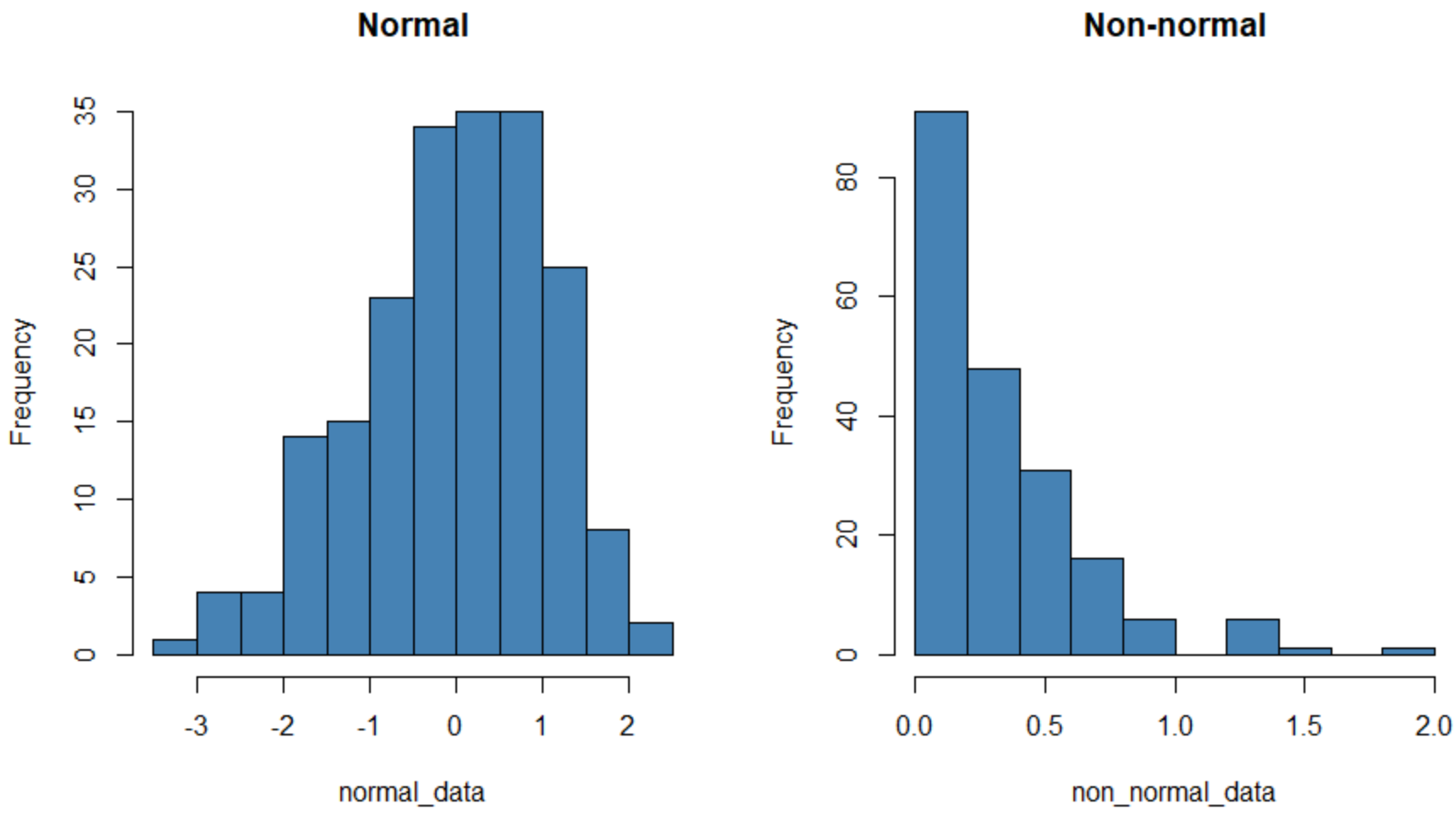
Het histogram aan de linkerkant toont een dataset die normaal verdeeld is (ruwweg „klokvormig“) en het histogram aan de rechterkant toont een dataset die niet normaal verdeeld is.

Methode 2: Maak een QQ-plot

De volgende code laat zien hoe u een QQ-plot maakt voor een normaal verdeelde en niet-normaal verdeelde gegevensset in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

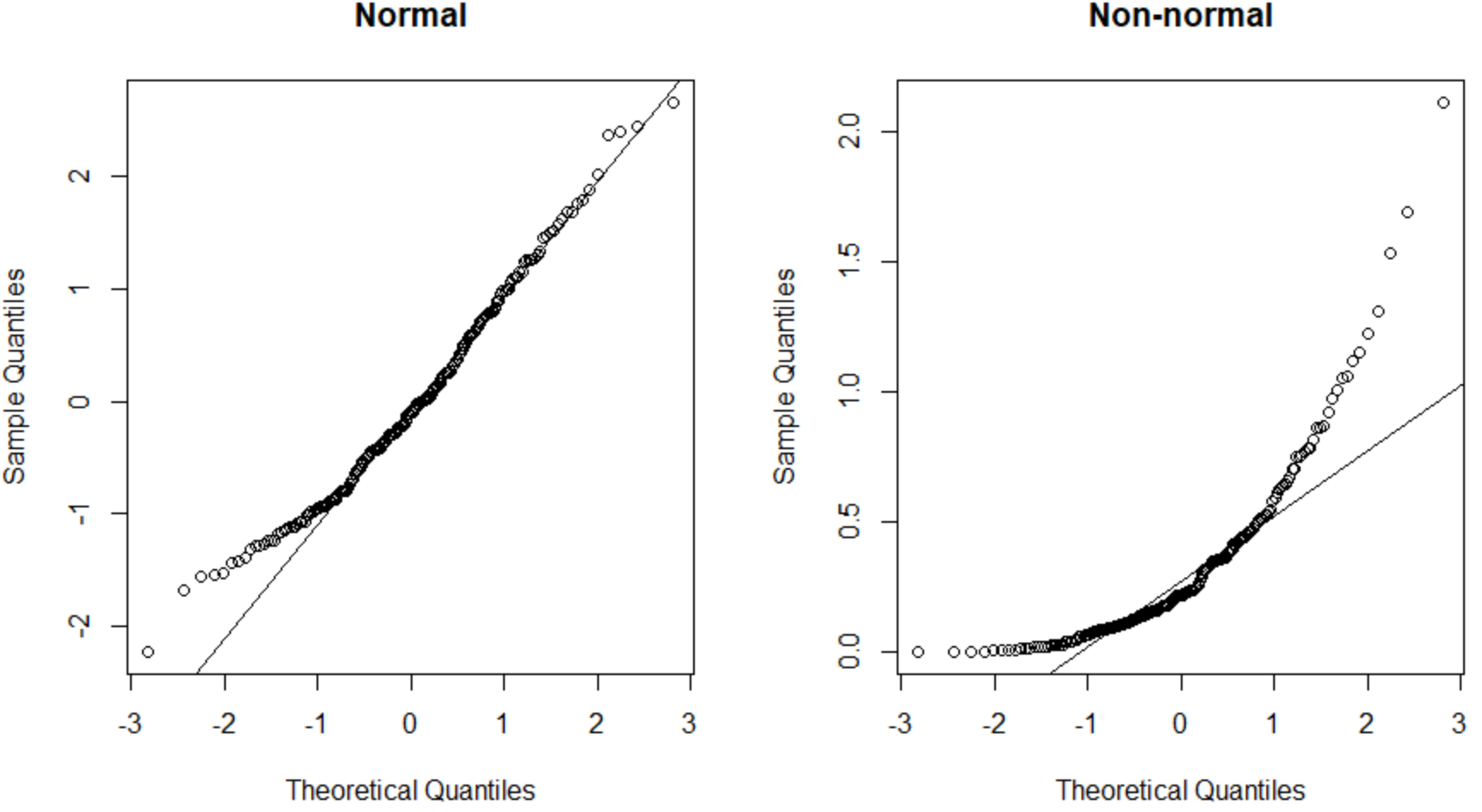
De QQ-plot aan de linkerkant presenteert een dataset die normaal verdeeld is (de punten vallen langs een rechte diagonale lijn) en de QQ-plot aan de rechterkant presenteert een dataset die niet normaal verdeeld is.

Methode 3: Voer een Shapiro-Wilk-test uit

De volgende code laat zien hoe u een Shapiro-Wilk-test uitvoert op een normaal verdeelde en niet-normaal verdeelde gegevensset in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

De p-waarde van de eerste test is niet minder dan 0,05, wat aangeeft dat de gegevens normaal verdeeld zijn.

De p-waarde van de tweede test is kleiner dan 0,05, wat aangeeft dat de gegevens niet normaal verdeeld zijn.

Methode 4: Voer een Kolmogorov-Smirnov-test uit

De volgende code laat zien hoe u een Kolmogorov-Smirnov-test uitvoert op een normaal verdeelde en niet-normaal verdeelde dataset in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

De p-waarde van de eerste test is niet minder dan 0,05, wat aangeeft dat de gegevens normaal verdeeld zijn.

De p-waarde van de tweede test is kleiner dan 0,05, wat aangeeft dat de gegevens niet normaal verdeeld zijn.

Hoe om te gaan met niet-normale gegevens

Als een bepaalde dataset niet normaal verdeeld is , kunnen we vaak een van de volgende transformaties uitvoeren om deze normaler verdeeld te maken:

1. Logtransformatie: transformeer x-waarden naar log(x) .

2. Vierkantsworteltransformatie: Transformeer de waarden van x naar √x .

3. Derdemachtsworteltransformatie: transformeer de waarden van x naar x ^1/3 .

Door deze transformaties uit te voeren, wordt de dataset doorgaans normaler verdeeld.

Lees deze tutorial om te zien hoe u deze transformaties in R kunt uitvoeren.

Aanvullende bronnen

Histogrammen maken in R
Hoe u een QQ-plot in R maakt en interpreteert
Hoe een Shapiro-Wilk-test uit te voeren in R
Hoe een Kolmogorov-Smirnov-test uit te voeren in R