Een normaliteitstest uitvoeren in google spreadsheets

Veel statistische tests gaan ervan uit dat de waarden in een dataset normaal verdeeld zijn.

Een van de eenvoudigste manieren om deze hypothese te testen is door een Jarque-Bera-test uit te voeren, een goodness-of-fit-test die bepaalt of de steekproefgegevens al dan niet scheefheid en kurtosis vertonen die consistent zijn met een normale verdeling.

Deze test maakt gebruik van de volgende aannames:

• H ₀ : Gegevens zijn normaal verdeeld.
• H _A : De gegevens zijn niet normaal verdeeld.

De JB- teststatistiek wordt gedefinieerd als:

JB =(n/6) * (S ² + (C ² /4))

Goud:

• n: het aantal waarnemingen in de steekproef
• S: de asymmetrie van het monster
• C: het flatterende exemplaar

Onder de nulhypothese van normaliteit is JB ~ X ² (2).

Als de p-waarde die overeenkomt met de teststatistiek onder een bepaald significantieniveau ligt (bijvoorbeeld α = 0,05), dan kunnen we de nulhypothese verwerpen en concluderen dat de gegevens niet normaal verdeeld zijn.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe u een Jarque-Bera-test kunt uitvoeren voor een bepaalde dataset in Google Spreadsheets.

Stap 1: Voer de gegevens in

Laten we eerst een nep-dataset maken met 15 waarden:

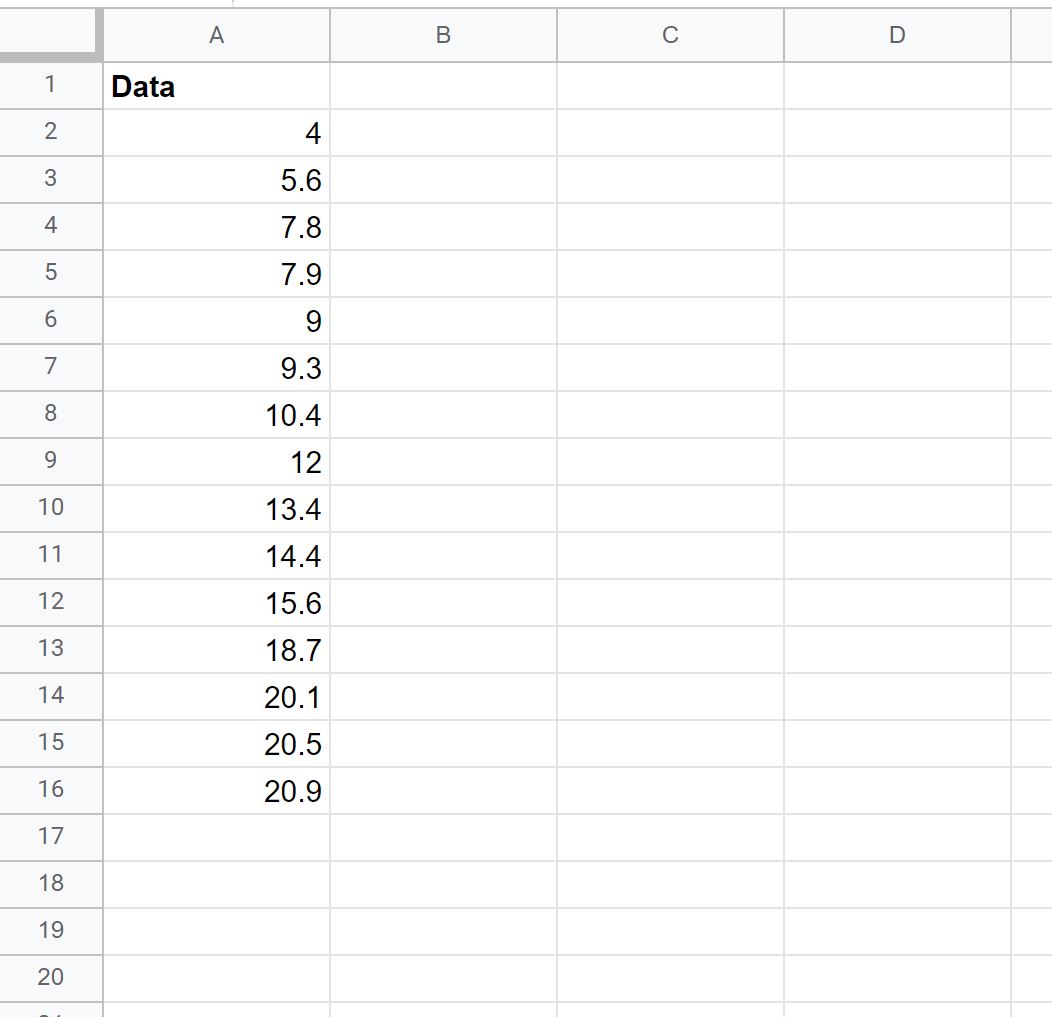
Stap 2: Bereken de teststatistiek

Vervolgens berekenen we de JB-teststatistiek.

Kolom E toont de gebruikte formules:

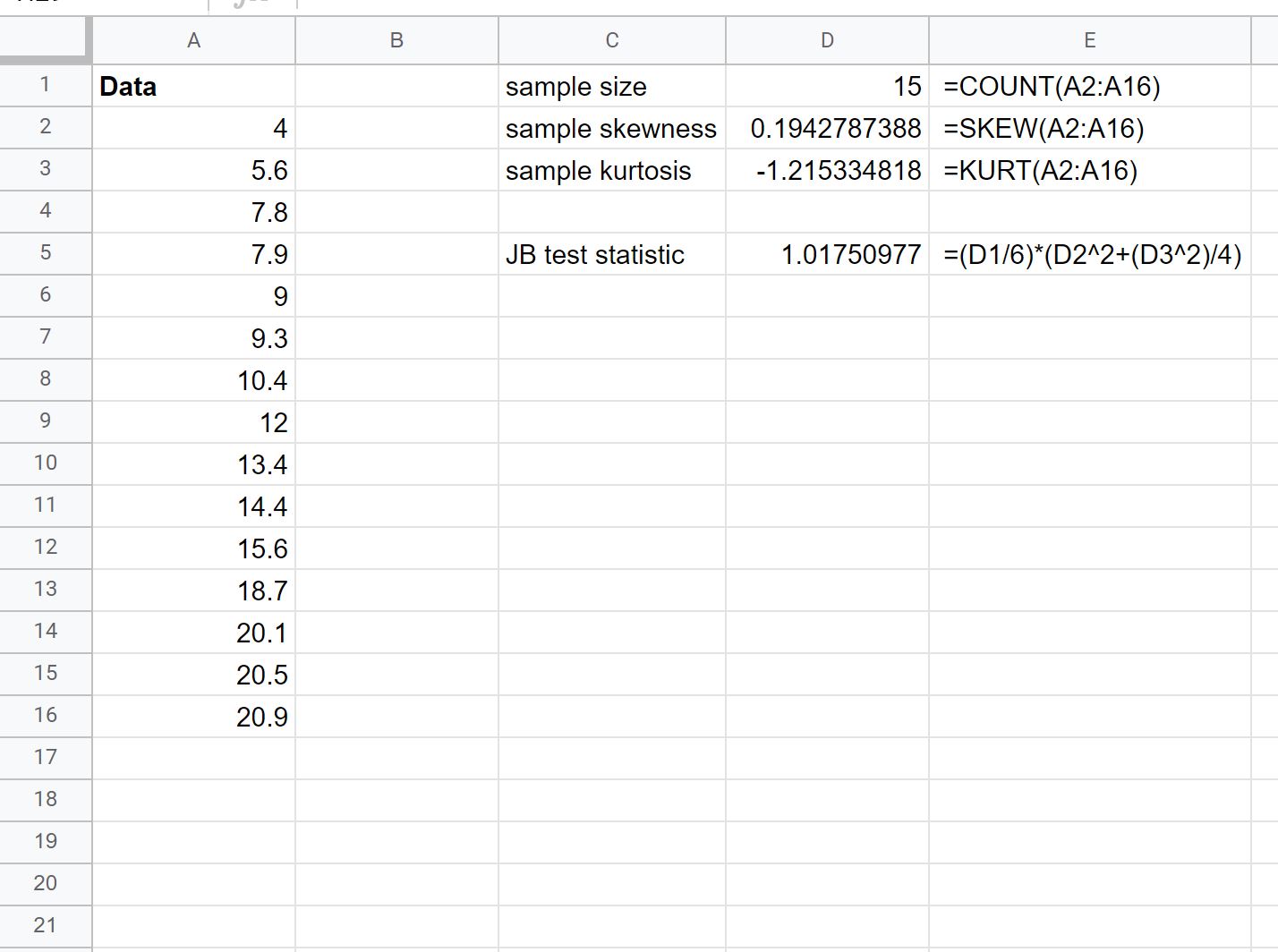
De teststatistiek blijkt 1,0175 te zijn.

Stap 3: Bereken de P-waarde

Onder de nulhypothese van normaliteit volgt de JB-teststatistiek een Chi-kwadraatverdeling met 2 vrijheidsgraden.

Om de p-waarde voor de test te vinden, gebruiken we dus de volgende formule:

=CHISQ.DIST.RT(JB-teststatistiek, 2)

De volgende schermafbeelding laat zien hoe u deze formule in de praktijk kunt gebruiken:

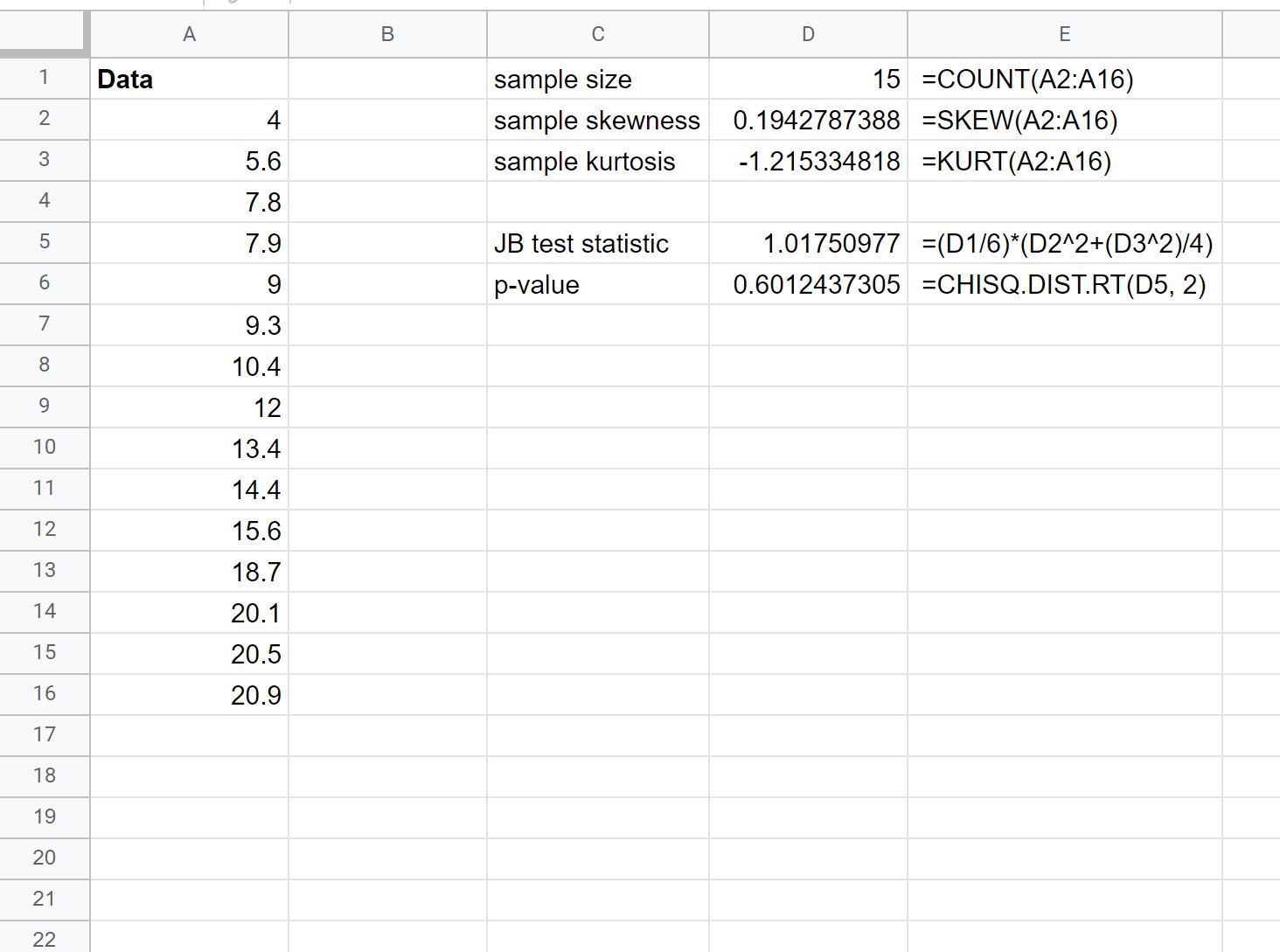
De p-waarde van de test is 0,601244 .

Onthoud dat deze Jarque-Bera-normaliteitstest de volgende hypothesen gebruikt:

• H ₀ : Gegevens zijn normaal verdeeld.
• H _A : De gegevens zijn niet normaal verdeeld.

Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we niet genoeg bewijs hebben om te zeggen dat de dataset niet normaal verdeeld is.

Met andere woorden, er kan worden aangenomen dat de gegevens normaal verdeeld zijn.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in Google Spreadsheets kunt uitvoeren:

Hoe u t-tests uitvoert in Google Spreadsheets
F-tests uitvoeren in Google Spreadsheets
Hoe u betrouwbaarheidsintervallen in Google Spreadsheets kunt berekenen