Hoe te testen op normaliteit in stata

Veel statistische tests vereisen dat een of meer variabelen normaal verdeeld zijn om de testresultaten betrouwbaar te maken.

In deze tutorial worden verschillende methoden uitgelegd die u kunt gebruiken om te testen op normaliteit tussen variabelen in Stata.

Voor elk van deze methoden gebruiken we de ingebouwde Stata-gegevensset genaamd auto . U kunt deze dataset laden met behulp van de volgende opdracht:

automatisch gebruik van het systeem

Methode 1: histogrammen

Een informele manier om te zien of een variabele normaal verdeeld is, is door een histogram te maken om de verdeling van de variabele weer te geven.

Als de variabele normaal verdeeld is , moet het histogram de vorm aannemen van een „bel“ met meer waarden nabij het midden en minder waarden aan de staarten.

We kunnen het hist- commando gebruiken om een histogram te maken voor de variabele verplaatsing :

bewegende geschiedenis

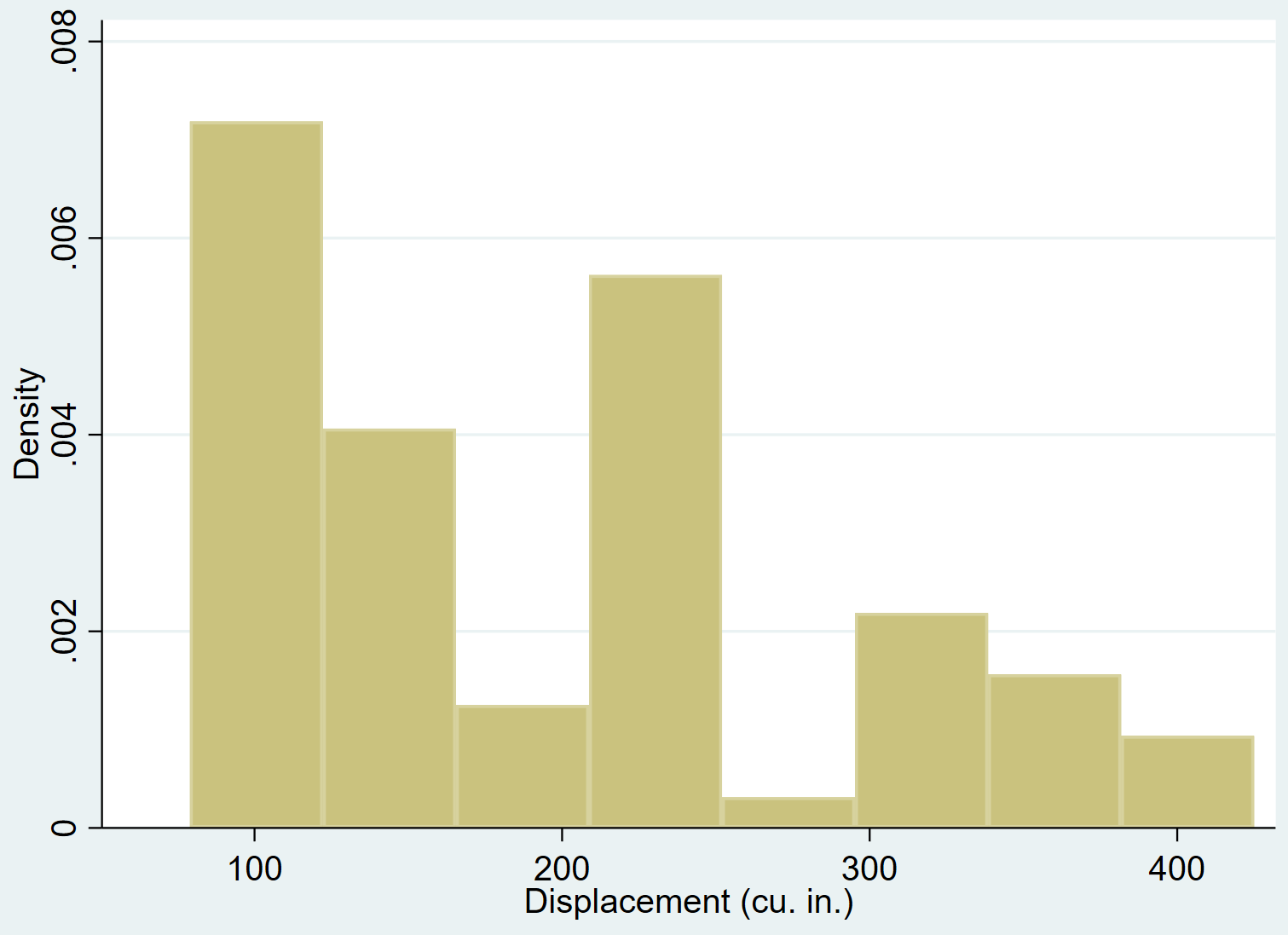
We kunnen een normale dichtheidscurve aan een histogram toevoegen met behulp van de normale opdracht:

bewegende geschiedenis, normaal

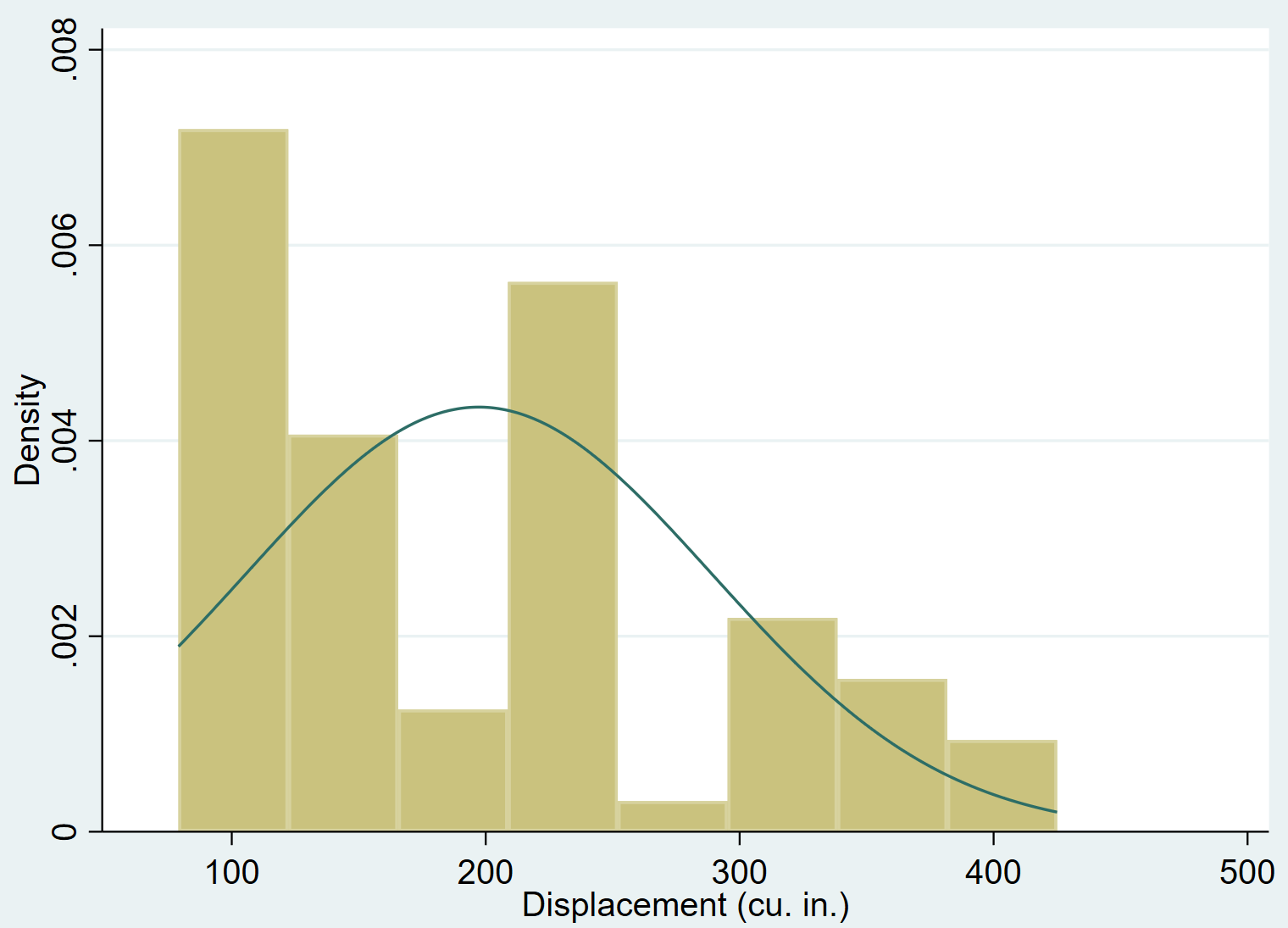
Het is vrij duidelijk dat de variabele verschuiving naar rechts scheef is (de meeste waarden zijn bijvoorbeeld geconcentreerd aan de linkerkant en een lange „staart“ van waarden strekt zich uit naar rechts) en volgt geen normale verdeling.

Gerelateerd:Links- en rechtsscheve verdelingen

Methode 2: Shapiro-Wilk-test

Een formele manier om op normaliteit te testen is door de Shapiro-Wilk-test te gebruiken.

De nulhypothese voor deze test is dat de variabele normaal verdeeld is. Als de p-waarde van de test onder een bepaald significantieniveau ligt (veel voorkomende keuzes zijn 0,01, 0,05 en 0,10), dan kunnen we de nulhypothese verwerpen en concluderen dat er voldoende bewijs is om te beweren dat de variabele niet normaal verdeeld is. .

*Deze test kan worden gebruikt als het totaal aantal waarnemingen tussen 4 en 2.000 ligt.

We kunnen het swilk- commando gebruiken om een Shapiro-Wilk-test uit te voeren op variabele verplaatsing :

soepele beweging

Zo interpreteert u het testresultaat:

Obs: 74. Dit is het aantal observaties dat in de test is gebruikt.

W: 0,92542. Dit is de teststatistiek voor de test.

Prob>z: 0,00031. Dit is de p-waarde die bij de teststatistiek hoort.

Omdat de p-waarde kleiner is dan 0,05, kunnen we de nulhypothese van de test verwerpen. We hebben voldoende bewijs om te zeggen dat de variabele verplaatsing niet normaal verdeeld is.

We kunnen de Shapiro-Wilk-test ook op meerdere variabelen tegelijk uitvoeren door meerdere variabelen op te sommen na het swilk- commando:

swilk verplaatsing mpg lengte

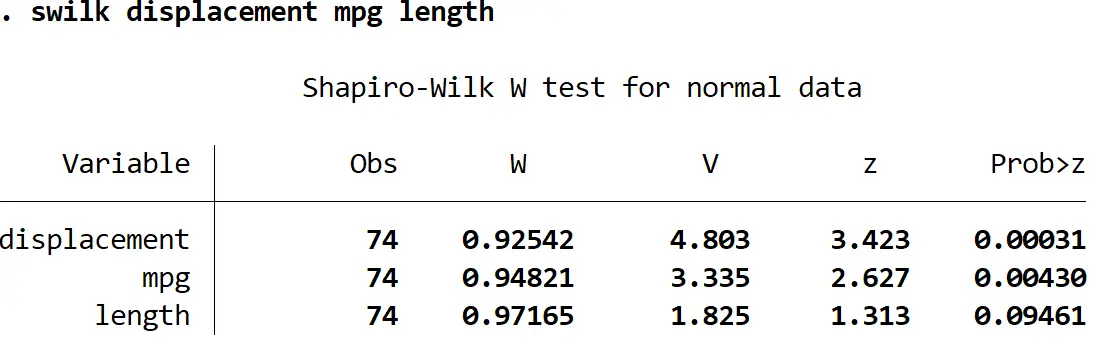
Als we een significantieniveau van 0,05 gebruiken, zouden we concluderen dat verplaatsing en mpg niet normaal verdeeld zijn, maar we hebben niet genoeg bewijs om te zeggen dat lengte niet normaal verdeeld is.

Methode 3: Shapiro-Francia-test

Een andere formele manier om op normaliteit te testen is door de Shapiro-Francia-test te gebruiken.

De nulhypothese voor deze test is dat de variabele normaal verdeeld is. Als de p-waarde van de test onder een bepaald significantieniveau ligt, kunnen we de nulhypothese verwerpen en concluderen dat er voldoende bewijs is om te zeggen dat de variabele niet normaal verdeeld is.

*Deze test kan worden gebruikt als het totaal aantal waarnemingen tussen de 10 en 5.000 ligt.

We kunnen het sfrancia- commando gebruiken om een Shapiro-Wilk-test uit te voeren op variabele verplaatsing :

bewegende sfrancia

Zo interpreteert u het testresultaat:

Obs: 74. Dit is het aantal observaties dat in de test is gebruikt.

W‘: 0,93011. Dit is de teststatistiek voor de test.

Waarschijnlijk>z: 0,00094. Dit is de p-waarde die bij de teststatistiek hoort.

Omdat de p-waarde kleiner is dan 0,05, kunnen we de nulhypothese van de test verwerpen. We hebben voldoende bewijs om te zeggen dat de variabele verplaatsing niet normaal verdeeld is.

Net als bij de Shapiro-Wilk-test kunt u de Shapiro-Francia-test op meerdere variabelen tegelijk uitvoeren door meerdere variabelen op te sommen na de opdracht sfrancia .

Methode 4: testen van scheefheid en kurtosis

Een andere manier om op normaliteit te testen is door de skewness- en kurtosis-test te gebruiken, die bepaalt of de skewness en kurtosis van een variabele al dan niet consistent zijn met de normale verdeling.

De nulhypothese voor deze test is dat de variabele normaal verdeeld is. Als de p-waarde van de test onder een bepaald significantieniveau ligt, kunnen we de nulhypothese verwerpen en concluderen dat er voldoende bewijs is om te zeggen dat de variabele niet normaal verdeeld is.

*Voor deze test zijn minimaal 8 waarnemingen vereist.

We kunnen het commando sktest gebruiken om een skewness- en kurtosis-test uit te voeren op de variabele verplaatsing :

de proef verplaatsen

Zo interpreteert u het testresultaat:

Obs: 74. Dit is het aantal observaties dat in de test is gebruikt.

bijvoeglijk naamwoord chi(2): 5,81. Dit is de chikwadraattoetsstatistiek voor de toets.

Prob>chi2: 0,0547. Dit is de p-waarde die bij de teststatistiek hoort.

Omdat de p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet genoeg bewijs om te zeggen dat bewegingen niet normaal verdeeld zijn.

Net als bij andere normaliteitstests kunt u de skewness- en kurtosis-test op meerdere variabelen tegelijk uitvoeren door meerdere variabelen op te sommen na de opdracht sktest .