Np-controlekaart

Von Dr.benjamin anderson August 1, 2023 Kwaliteitsmanagement Keine Kommentare

In dit artikel laten we u zien wat een NP-controlediagram is en waarvoor deze wordt gebruikt. Daarnaast krijg je een opgeloste oefening te zien waarin we uitleggen hoe je een NP-controlediagram maakt.

Wat is een NP-controlediagram?

Een NP-controlediagram , of eenvoudigweg NP-diagram , is een grafiek waarin het aantal defecte eenheden uit verschillende monsters van constante grootte wordt weergegeven.

Een NP-controlediagram wordt gebruikt om te controleren of het aantal defecte eenheden in een proces de controlelimieten niet overschrijdt.

Een NP-controlekaart kan bijvoorbeeld worden gebruikt om de evolutie van defecte producten die door een productieproces worden geproduceerd, te analyseren. Op deze manier kunnen we weten dat er een probleem is in het productieproces wanneer het aantal defecte producten de controlelimieten overschrijdt.

Het is belangrijk op te merken dat, in tegenstelling tot een P-controlediagram, het NP-controlediagram niet het aandeel defecte eenheden bewaakt, maar eerder het aantal defecte eenheden. Bovendien moet de grootte van alle monsters hetzelfde zijn.

Hoe u een NP-controlediagram maakt

De stappen die u moet volgen om een NP-controlediagram te maken, zijn als volgt:

Monsters nemen : Allereerst moet u verschillende monsters nemen om de evolutie van het aantal defecte eenheden in de grafiek te zien. Monsters moeten dezelfde grootte hebben. Bovendien wordt aanbevolen dat er ten minste 20 monsters worden genomen en dat de monstergrootte groter is dan 50.
Tel het aantal defecte eenheden : Voor elk monster moet het aantal eenheden met minstens één defect worden bepaald.
Bereken de gemiddelde waarde van het aandeel : Uit alle bestudeerde elementen moet u het totale aandeel defecte eenheden berekenen.

$\overline{p}=\cfrac{\text{N\'umero total de unidades defectuosas}}{\text{N\'umero total de unidades}}$

Bereken de controlelimieten van de NP-kaart : Voor elk getest monster moet u de controlelimieten vinden met behulp van de volgende formules:

$\displaystyle LCS=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})}$

$\displaystyle LCI=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})}$

Goud

$LCS$

$LCI$

zijn respectievelijk de bovenste en onderste controlelimieten,

$\overline{p}$

is de gemiddelde waarde van het aandeel defecten en

$n$

is de steekproefomvang.

Zet de waarden in de grafiek : Nu moet u de waarden van het aantal verkregen defecten samen met de controlelimieten die in de vorige stap zijn berekend, in een grafiek weergeven.
Analyseer het NP-controlediagram : Ten slotte hoeft u alleen nog maar te controleren of geen enkele waarde buiten de controlegrenzen van het diagram valt en dat het proces daarom onder controle is. Anders moeten er maatregelen worden genomen om het productieproces te corrigeren.

Voorbeeld van een NP-controlediagram

Vervolgens zullen we zien hoe u een NP-controlediagram kunt maken met behulp van een stapsgewijs opgelost voorbeeld.

Een industrieel bedrijf verzamelde monsters van 100 eenheden en analyseerde het aantal defecte onderdelen in elk monster. De geregistreerde waarden zijn te zien in de volgende tabel. Maak een NP-controlediagram met de verkregen gegevens.

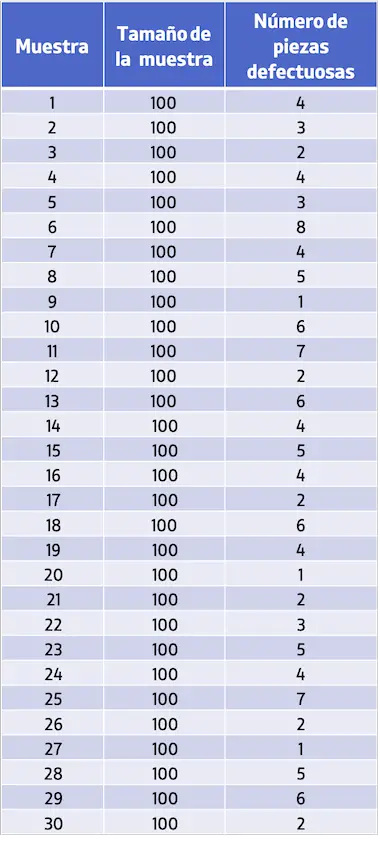
Zoals u kunt zien, hebben alle onderzochte monsters dezelfde grootte en bovendien is de steekproefomvang groter dan 50 eenheden, zodat aan de kenmerken wordt voldaan om een NP-controlediagram te kunnen maken.

Het eerste dat we moeten berekenen om de NP-grafiek te maken, is dus het gemiddelde aantal defecte eenheden. Om dit te doen, past u eenvoudig de volgende formule toe:

$\overline{p}=\cfrac{\text{N\'umero total de unidades defectuosas}}{\text{N\'umero total de unidades}}=\cfrac{118}{30\cdot 100}=0,039$

We berekenen nu de NP-kaartcontrolelimieten met de formules die we hierboven zagen:

$\begin{aligned}\displaystyle LCS&=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039+3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=9,76\end{aligned}$

$\begin{aligned}\displaystyle LCI&=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039-3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=-1,9\end{aligned}$

De onderste controlegrens is negatief geworden, wat geen zin heeft, aangezien defecte negatieve eenheden niet kunnen worden vervaardigd. Daarom stellen we de onderste controlelimiet op 0.

Nadat we de controlelimieten hebben berekend, zetten we alle waarden in het NP-controlediagram in kaart:

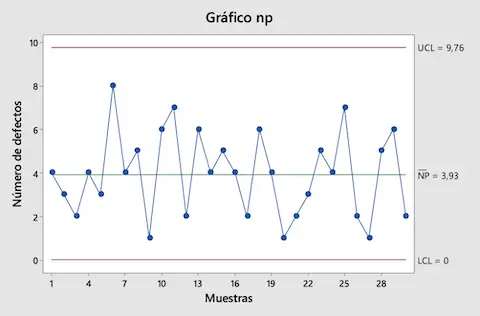
Zoals u kunt zien in de NP-grafiek liggen alle waarden die uit de monsters zijn verzameld binnen de controlelimieten, dus er wordt geconcludeerd dat het productieproces onder controle is.

Andere soorten controlediagrammen

Naast het NP-controlediagram zijn er binnen kwaliteitsmanagement nog andere typen attribuutcontrolediagrammen:

P-controlekaart : Het aandeel producten met gebreken wordt gecontroleerd.
Stuurkaart C : Het aantal optredende fouten wordt bewaakt.
Controlediagram U : Het aantal defecten wordt gecontroleerd zoals in diagram C, maar de steekproefomvang is variabel.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder