Wat is nulde-ordecorrelatie?

In de statistiek vertelt de correlatie tussen twee variabelen ons over de relatie tussen deze twee variabelen.

Een van de meest basale soorten correlatie staat bekend als nulde-orde correlatie , wat verwijst naar de correlatie tussen twee variabelen zonder te controleren op de mogelijke invloed van andere variabelen.

Een voorbeeld van dit type correlatie is de Pearson-correlatiecoëfficiënt , die de lineaire associatie tussen twee variabelen meet en waarden tussen -1 en 1 kan aannemen, waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Hoe verder de correlatie van nul verwijderd is, hoe sterker de associatie tussen de twee variabelen.

Eerste en tweede orde correlaties

Als we de correlatie tussen twee variabelen A en B berekenen terwijl we controleren voor de invloed van een derde variabele C, zouden we de correlatie tussen A en B een eerste-orde correlatie noemen.

Op dezelfde manier zouden we, als we de correlatie tussen twee variabelen A en B berekenen terwijl we controleren voor de invloed van variabelen C en D, de correlatie tussen A en B een tweede-orde correlatie noemen.

Voorbeeld van nulde-ordecorrelatie

Laten we zeggen dat we de volgende gegevensset hebben die het aantal uren aan studeren toont en het cijfer dat 10 verschillende studenten op het examen hebben behaald:

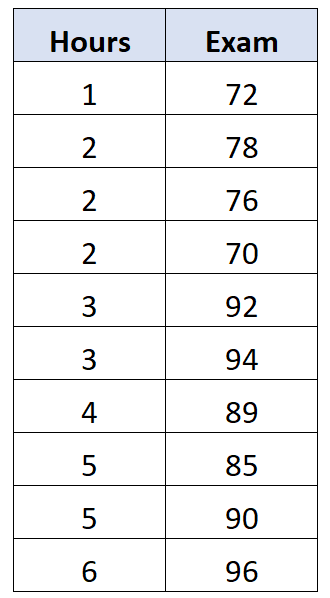
Het blijkt dat de correlatie tussen deze twee variabelen 0,762 bedraagt. Dit zou worden beschouwd als een correlatie van de nulde orde tussen de twee variabelen, omdat we niet controleren voor de potentiële invloed van een derde variabele.

In werkelijkheid is het echter mogelijk dat andere factoren de relatie tussen deze twee variabelen beïnvloeden.

Het huidige cijfer van de leerling in de klas kan bijvoorbeeld een effect hebben op de examenscore. Stel dat wij ook toegang hebben tot deze gegevens:

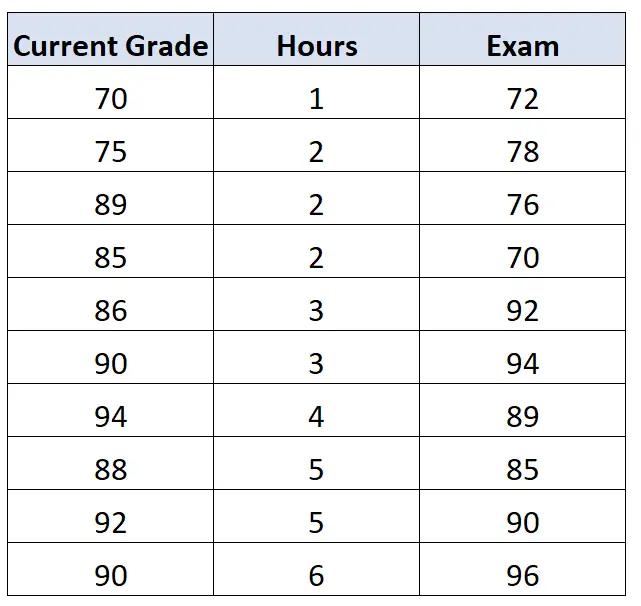
Als we vervolgens de correlatie tussen uren en examen berekenen en daarbij controleren voor het effect van het huidige cijfer , vinden we dat de eerste orde correlatie tussen uren en examen 0,578 is.

Dit betekent dat er nog steeds een vrij sterke positieve correlatie bestaat tussen het aantal gestudeerde uren en het examencijfer, zelfs na controle voor het effect van het huidige cijfer van de leerling in de klas.

Opmerking: Eerste-ordecorrelatie wordt ook wel gedeeltelijke correlatie genoemd . In deze tutorial wordt uitgelegd hoe u gedeeltelijke correlaties in Excel kunt berekenen.

Nulde-correlaties in een correlatiematrix

we maken een correlatiematrix Wanneer voor een reeks variabelen de correlatiecoëfficiënten die in de matrix worden weergegeven altijd correlaties van de nulde orde zijn, omdat ze eenvoudigweg de correlaties zijn tussen elke paarsgewijze combinatie van variabelen zonder rekening te houden met de invloed van andere variabelen.

Beschouw bijvoorbeeld onze dataset uit het vorige voorbeeld:

Als we voor deze dataset een correlatiematrix zouden maken, zou deze er als volgt uitzien:

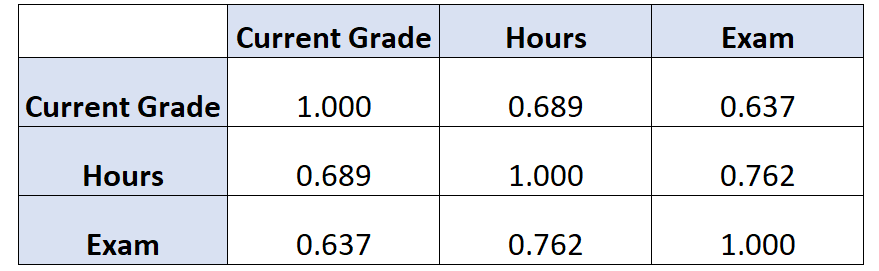
De manier om dit te interpreteren is:

• De correlatie tussen het huidige cijfer en het aantal gestudeerde uren is 0,689 .
• De correlatie tussen de huidige score en de score behaald op het examen is 0,637 .
• De correlatie tussen het aantal gestudeerde uren en de examenscore bedraagt 0,762 .

Elk van deze correlaties is een correlatie van de nulde orde .

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over correlatiecoëfficiënten:

Inleiding tot de Pearson-correlatiecoëfficiënt
Hoe een correlatiematrix te lezen
Hoe gedeeltelijke correlatie in Excel te berekenen