De nulhypothese voor anova-modellen begrijpen

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Een eenrichtings-ANOVA gebruikt de volgende nul- en alternatieve hypothesen:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (alle groepsgemiddelden zijn gelijk)
• H _A : Minstens één groepsgemiddelde is anders   rest

Om te beslissen of we de nulhypothese al dan niet moeten verwerpen, moeten we verwijzen naar de p-waarde in het resultaat van de ANOVA-tabel.

Als de p-waarde onder een bepaald significantieniveau ligt (bijvoorbeeld 0,05), kunnen we de nulhypothese verwerpen en concluderen dat niet alle groepsgemiddelden gelijk zijn.

Een tweerichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen die aan twee variabelen zijn toegewezen (soms „factoren“ genoemd).

Een tweerichtings-ANOVA test tegelijkertijd drie nulhypothesen:

• Alle groepsgemiddelden zijn gelijk op elk niveau van de eerste variabele
• Alle groepsgemiddelden zijn gelijk op elk niveau van de tweede variabele
• Er is geen interactie-effect tussen de twee variabelen

Om te beslissen of we elke nulhypothese al dan niet moeten verwerpen, moeten we verwijzen naar de p-waarden in het resultaat van de tweeweg-ANOVA-tabel.

De volgende voorbeelden laten zien hoe u kunt beslissen of u de nulhypothese al dan niet verwerpt bij een eenrichtings-ANOVA en een tweerichtings-ANOVA.

Voorbeeld 1: Eenrichtings-ANOVA

Stel dat we willen weten of drie verschillende toetsvoorbereidingsprogramma’s al dan niet tot verschillende gemiddelde scores op een bepaald examen leiden. Om dit te testen werven we 30 studenten om mee te doen aan een onderzoek en verdelen ze in drie groepen.

Studenten in elke groep worden willekeurig toegewezen om de komende drie weken een van de drie toetsvoorbereidingsprogramma’s te gebruiken ter voorbereiding op een examen. Aan het einde van de drie weken leggen alle studenten hetzelfde examen af.

Hieronder vindt u de examenresultaten per groep:

Wanneer we deze waarden invoeren in de one-way ANOVA-calculator , ontvangen we de volgende ANOVA-tabel als uitvoer:

Merk op dat de p-waarde 0,11385 is.

Voor dit specifieke voorbeeld zouden we de volgende nul- en alternatieve hypothesen gebruiken:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (de gemiddelde examenscore voor elke groep is gelijk)
• H _A : Minstens één groepsgemiddelde is anders   rest

Omdat de p-waarde van de ANOVA-tabel niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Dit betekent dat we onvoldoende bewijs hebben om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde examenscores van de drie groepen.

Voorbeeld 2: Tweeweg-ANOVA

Stel dat een botanicus wil weten of de plantengroei wordt beïnvloed door blootstelling aan zonlicht en de frequentie van water geven.

Ze plant 40 zaden en laat ze twee maanden lang groeien onder verschillende omstandigheden wat betreft blootstelling aan de zon en waterfrequentie. Na twee maanden registreert ze de hoogte van elke plant. De resultaten worden hieronder weergegeven:

In de bovenstaande tabel zien we dat er onder elke combinatie van omstandigheden vijf planten werden gekweekt.

Er werden bijvoorbeeld vijf planten gekweekt met dagelijks water en zonder zonlicht en hun hoogten na twee maanden waren 4,8 inch, 4,4 inch, 3,2 inch, 3,9 inch en 4,4 inch:

Ze voert een tweeweg-ANOVA uit in Excel en bekomt het volgende resultaat:

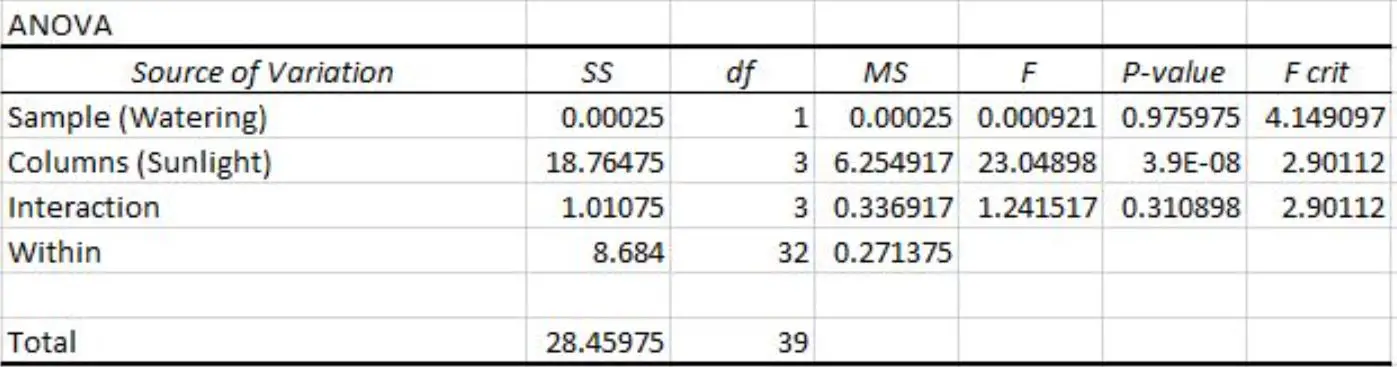
We kunnen de volgende p-waarden zien in het resultaat van de tweeweg-ANOVA-tabel:

• De p-waarde voor de bewateringsfrequentie is 0,975975 . Dit is niet statistisch significant op het significantieniveau van 0,05.
• De p-waarde voor blootstelling aan de zon is 3,9E-8 (0,000000039) . Dit is statistisch significant op het significantieniveau van 0,05.
• De p-waarde voor de interactie tussen de waterfrequentie en de blootstelling aan de zon is 0,310898 . Dit is niet statistisch significant op het significantieniveau van 0,05.

Deze resultaten geven aan dat blootstelling aan de zon de enige factor is met een statistisch significant effect op de planthoogte.

En omdat er geen interactie-effect is, is het effect van blootstelling aan de zon consistent op elk niveau van de bewateringsfrequentie.

Simpel gezegd: of een plant dagelijks of wekelijks water krijgt, heeft geen invloed op de invloed van blootstelling aan de zon op een plant.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over ANOVA-modellen:

Hoe F-waarde en P-waarde in ANOVA te interpreteren
Hoe de som van de kwadraten in ANOVA te berekenen
Wat betekent een hoge F-waarde in ANOVA?