Hoe oddsratio’s te interpreteren

In de statistiek verwijst waarschijnlijkheid naar de kans dat een gebeurtenis plaatsvindt. Het wordt als volgt berekend:

WAARSCHIJNLIJKHEID:

P(gebeurtenis) = (# wenselijke uitkomsten) / (# mogelijke uitkomsten)

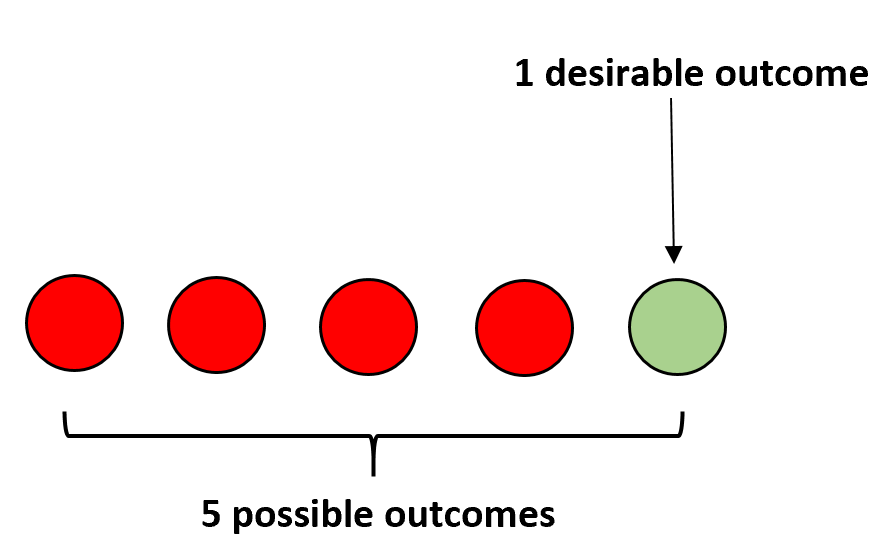
Stel dat we vier rode ballen en één groene bal in een zak hebben. Als je je ogen sluit en willekeurig een bal selecteert, wordt de kans dat je een groene bal kiest als volgt berekend:

P(groen) = 1/5 = 0,2 .

De kans dat een gebeurtenis plaatsvindt, kan als volgt worden berekend:

KANSEN:

Kansen (gebeurtenis) = P (gebeurtenis vindt plaats) / 1-P (gebeurtenis vindt plaats)

De kans dat je een groene bal schiet, is bijvoorbeeld (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .

De odds ratio is de verhouding tussen twee kansen.

GELUK RAPPORT:

Odds Ratio = Kans op gebeurtenis A / Kans op gebeurtenis B

We kunnen bijvoorbeeld de odds ratio berekenen tussen het kiezen van een rode bal en een groene bal.

De kans op het trekken van een rode bal is 4/5 = 0,8 .

De kans op het trekken van een rode bal is (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .

De oddsratio voor het kiezen van een rode bal boven een groene bal wordt als volgt berekend:

Kansen (rood) / Kansen (groen) = 4 / 0,25 = 16 .

De kans op het schieten van een rode bal is dus 16 keer groter dan de kans op het schieten van een groene bal.

Wanneer worden odds ratio’s in de echte wereld gebruikt?

In de echte wereld worden odds ratio’s gebruikt in verschillende contexten waarin onderzoekers de kansen willen vergelijken dat twee gebeurtenissen plaatsvinden. Hier zijn enkele voorbeelden.

Voorbeeld #1: Kansverhoudingen interpreteren

Onderzoekers willen weten of een nieuwe behandeling de kans vergroot dat een patiënt een positief gezondheidsresultaat ervaart in vergelijking met een bestaande behandeling. De volgende tabel toont het aantal patiënten dat een positief of negatief gezondheidsresultaat ervoer, afhankelijk van de behandeling.

De kans dat een patiënt een positief resultaat ervaart met de nieuwe behandeling kan als volgt worden berekend:

Kans = P(positief) / 1 – P(positief) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25

De kans dat een patiënt een positief resultaat ervaart met de bestaande behandeling kan als volgt worden berekend:

Kans = P(positief) / 1 – P(positief) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875

De odds ratio voor het bereiken van een positief resultaat met de nieuwe behandeling in vergelijking met de bestaande behandeling kan dus als volgt worden berekend:

Odds-ratio = 1,25 / 0,875 = 1,428 .

Wij interpreteren dit zo dat de kans dat een patiënt een positief resultaat heeft bij gebruik van de nieuwe behandeling 1,428 keer groter is dan de kans dat een patiënt een positief resultaat heeft bij gebruik van de bestaande behandeling.

Met andere woorden: de kans op een positief resultaat wordt met de nieuwe behandeling met 42,8% vergroot.

Voorbeeld #2: Kansverhoudingen interpreteren

Marketeers willen weten of een advertentie ertoe leidt dat klanten een bepaald artikel vaker kopen dan een andere advertentie. Dus laten ze elke advertentie aan 100 mensen zien. In de volgende tabel ziet u het aantal mensen dat het artikel heeft gekocht, op basis van de advertentie die ze hebben gezien:

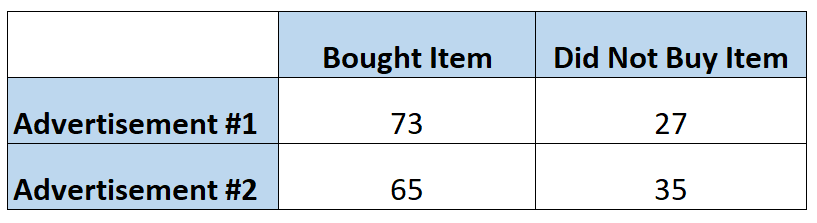
De kans dat iemand het artikel koopt nadat hij de eerste advertentie heeft gezien, kan als volgt worden berekend:

Odds = P(gekocht) / 1 – P(gekocht) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704

De kans dat iemand het artikel koopt nadat hij de tweede advertentie heeft gezien, kan als volgt worden berekend:

Odds = P(gekocht) / 1 – P(gekocht) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857

De oddsratio voor een klant die het artikel koopt nadat hij de eerste advertentie heeft gezien versus een aankoop nadat hij de tweede advertentie heeft gezien, kan dus als volgt worden berekend:

Odds-ratio = 2,704 / 1,857 = 1,456 .

We interpreteren dit zo dat de kans dat een individu het artikel koopt na het zien van de eerste advertentie 1,456 maal de kans is dat een individu het artikel koopt na het zien van de tweede advertentie.

Met andere woorden, de kansen om het artikel te kopen worden dankzij de eerste aanbieding met 45,6% verhoogd.

Aanvullende bronnen

Hoe u de oddsratio en het relatieve risico in Excel kunt berekenen
Hoe interpreteer je een odds ratio kleiner dan 1?
Hoe het relatieve risico te interpreteren