Odds ratio versus relatief risico: wat is het verschil?

Twee termen die studenten vaak verwarren in de statistiek zijn odds ratio en relatief risico .

We gebruiken deze twee statistieken vaak bij het analyseren van een tabel van 2 bij 2, die de volgende indeling heeft:

De odds ratio vertelt ons de verhouding tussen de waarschijnlijkheid dat een gebeurtenis optreedt in een behandelgroep en de waarschijnlijkheid dat een gebeurtenis optreedt in een controlegroep. Het wordt als volgt berekend:

Odds-ratio = (A*D) / (B*C)

Het relatieve risico vertelt ons de verhouding tussen de waarschijnlijkheid dat een gebeurtenis zich voordoet in een behandelgroep en de waarschijnlijkheid dat een gebeurtenis zich voordoet in een controlegroep. Het wordt als volgt berekend:

Relatief risico = [A/(A+B)] / [C/(C+D)]

Kortom, hier is het verschil:

• Een odds ratio is een verhouding van twee odds .
• Relatief risico is een verhouding tussen twee kansen .

Het volgende voorbeeld laat zien hoe u een oddsratio en een relatief risico in een reële situatie kunt berekenen en interpreteren.

Voorbeeld: berekening van de odds ratio en het relatieve risico

Veronderstel dat 100 basketbalspelers een nieuw trainingsprogramma gebruiken en dat 100 spelers een oud trainingsprogramma gebruiken. Aan het einde van het programma testen we elke speler om te zien of hij of zij slaagt voor een bepaalde vaardigheidstest.

De volgende tabel toont het aantal spelers dat wel of niet slaagde, gebaseerd op het programma dat ze gebruikten:

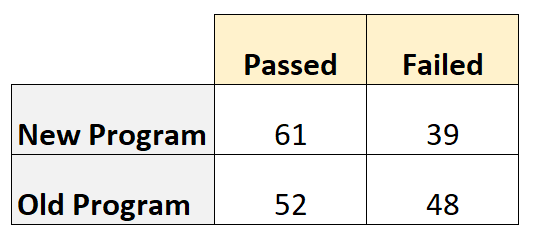
De oddsratio wordt als volgt berekend:

• Odds-ratio = (A*D) / (B*C)
• Odds-ratio = (61*48) / (39*52)
• Odds-ratio = 1,44

We zouden dit zo interpreteren dat de kans dat een speler slaagt voor de test met het nieuwe programma 1,44 keer groter is dan de kans dat een speler de test haalt met het oude programma.

Met andere woorden: de kans dat een speler de test doorstaat, neemt toe door het gebruik van het nieuwe programma.

Het relatieve risico wordt berekend als

• Relatief risico = [A/(A+B)] / [C/(C+D)]
• Relatief risico = [61/(61+39)] / [52/(52+48)]
• Relatief risico = 1,17

We zouden dit zo interpreteren dat de verhouding tussen de kans dat een speler de test met het nieuwe programma doorstaat en het oude programma 1,17 bedraagt.

Omdat deze waarde groter is dan 1, vertelt dit ons dat de kans op succes groter is in het nieuwe programma dan in het oude programma.

We kunnen dit ook zien door direct de kans te berekenen dat een speler onder elk programma slaagt:

Kans op succes onder nieuw programma = 61/100 = 61%

Kans op succes onder het oude programma = 52 / 100 = 52%

Door de verhouding tussen deze kansen te nemen, kunnen we het relatieve risico berekenen als 61% / 52% = 1,17 .

Merk op dat de odds ratio en het relatieve risico beide groter zijn dan 1, wat ons vertelt dat de kans op het meemaken van een gebeurtenis (bijvoorbeeld het slagen voor de vaardigheidstest) groter is in de behandelgroep dan in de controlegroep.

De oddsratio en het relatieve risico geven ons vergelijkbare informatie, maar we interpreteren elke waarde iets anders.

Speciaal:

• De odds ratio vertelt ons dat de kansen om te slagen voor de vaardigheidstest groter zijn onder het nieuwe programma.
• Het relatieve risico vertelt ons dat de kans om te slagen voor de vaardigheidstest groter is onder het nieuwe programma.

Als we beide meetwaarden gebruiken, kunnen we gemakkelijk zien dat het nieuwe programma beter is dan het oude.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over oddsratio’s en relatief risico:

Hoe oddsratio’s te interpreteren
Hoe het relatieve risico te interpreteren
Hoe u de oddsratio en het relatieve risico in Excel kunt berekenen