Hoe u oddsratio's in sas kunt berekenen (met voorbeeld)

In de statistieken vertelt een odds ratio ons de verhouding tussen de kans dat een gebeurtenis zich voordoet in een behandelgroep en de kans dat een gebeurtenis zich voordoet in een controlegroep.

We berekenen vaak een oddsratio bij het uitvoeren van analyses op een tafel van 2 bij 2, die het volgende formaat heeft:

Om een odds ratio in SAS te berekenen, kunnen we de PROC FREQ- instructie gebruiken.

Het volgende voorbeeld laat zien hoe u deze verklaring in de praktijk kunt gebruiken.

Voorbeeld: een odds ratio berekenen in SAS

Laten we zeggen dat 50 basketbalspelers een nieuw trainingsprogramma gebruiken en 50 spelers een oud trainingsprogramma gebruiken. Aan het einde van het programma testen we elke speler om te zien of hij of zij slaagt voor een bepaalde vaardigheidstest.

De volgende tabel toont het aantal spelers dat wel of niet slaagde, gebaseerd op het programma dat ze gebruikten:

Laten we zeggen dat we een oddsratio willen berekenen om de kansen te vergelijken dat een speler de vaardigheidstest haalt met het nieuwe programma en met het oude programma.

We kunnen de volgende syntaxis gebruiken met PROC FREQ in SAS met de chisq- en relrisk- instructies om deze oddsratio samen met de relatieve risicowaarden te berekenen:

 /*create dataset*/
data my_data;
    input result $program $count;
    datalines ;
Passed New 34
Passed Old 39
_Failed New 16
_Failed Old 11
;
run ;
/*calculate odds ratio*/
proc freq data =my_data;
    weightcount ;
    tables program * result / chisq relrisk ;
run ;

De eerste tabel met het resultaat toont de frequentie van elke combinatie van categorische variabelen:

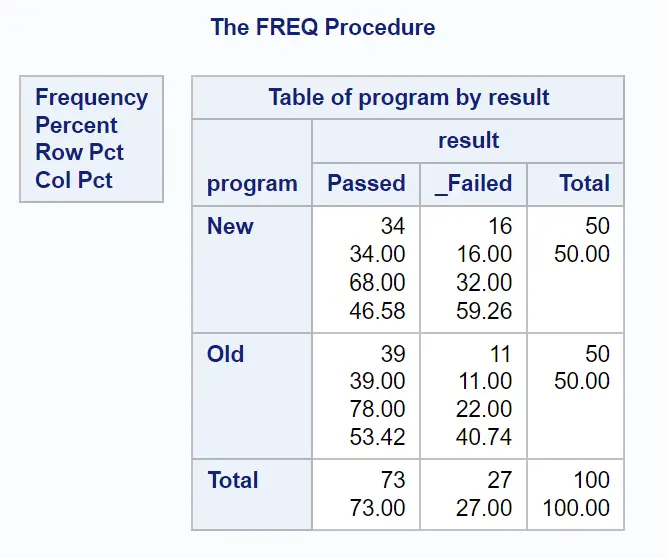
De laatste tabel met het resultaat toont de odds ratio die ons interesseert:

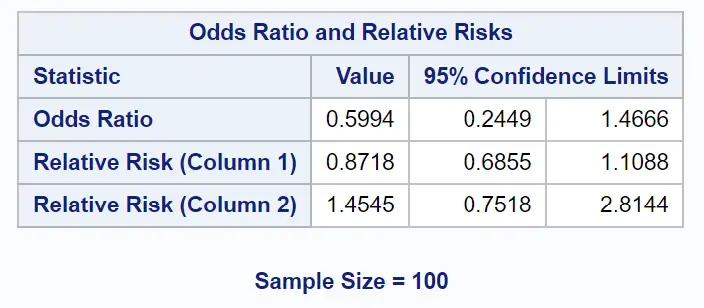
De oddsratio blijkt 0,5994 te zijn.

Wij interpreteren dit zo dat de kans dat een speler slaagt voor de test met het nieuwe programma slechts 0,5994 keer zo groot is als de kans dat een speler de test haalt met het oude programma.

Met andere woorden: de kans dat een speler de test doorstaat, wordt feitelijk met ongeveer 40,06% verkleind door het gebruik van het nieuwe programma.

We kunnen ook de waarden in de kolommen Resultaat 95% betrouwbaarheidslimieten gebruiken om het volgende 95% betrouwbaarheidsinterval voor de oddsratio te construeren:

95% betrouwbaarheidsinterval voor de oddsratio: [0,2449, 1,4666] .

We zijn er 95% zeker van dat de werkelijke odds ratio tussen het nieuwe en het oude trainingsprogramma binnen dit interval ligt.

Omdat het betrouwbaarheidsinterval de odds ratio-waarde van 1 bevat, betekent dit dat de odds ratio niet statistisch significant is.

Met andere woorden, we weten uit de odds ratio dat de kans op succes van een speler bij gebruik van het nieuwe programma kleiner is dan de kans op succes bij gebruik van het oude programma, maar het verschil tussen deze kansen is feitelijk niet statistisch significant.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over oddsratio’s:

Het verschil tussen de oddsratio en het relatieve risico
De complete gids: Hoe u oddsratio’s kunt rapporteren
Hoe u een betrouwbaarheidsinterval voor een oddsratio kunt berekenen