Ols-regressie uitvoeren in r (met voorbeeld)

Gewone kleinste kwadratenregressie (OLS) is een methode waarmee we een lijn kunnen vinden die de relatie tussen een of meer voorspellende variabelen en eenresponsvariabele het beste beschrijft.

Met deze methode kunnen we de volgende vergelijking vinden:

ŷ = _b0 + _b1 x

Goud:

• ŷ : De geschatte responswaarde
• b ₀ : De oorsprong van de regressielijn
• b ₁ : De helling van de regressielijn

Deze vergelijking kan ons helpen de relatie tussen de voorspeller en de responsvariabele te begrijpen, en kan worden gebruikt om de waarde van een responsvariabele te voorspellen, gegeven de waarde van de voorspellende variabele.

In het volgende stapsgewijze voorbeeld ziet u hoe u OLS-regressie uitvoert in R.

Stap 1: Creëer de gegevens

Voor dit voorbeeld maken we een dataset met de volgende twee variabelen voor 15 studenten:

• Totaal aantal bestudeerde uren
• Examenresultaat

We voeren een OLS-regressie uit, waarbij we uren gebruiken als voorspellende variabele en examenscore als responsvariabele.

De volgende code laat zien hoe u deze nep-dataset in R kunt maken:

 #create dataset
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Stap 2: Visualiseer de gegevens

Voordat we een OLS-regressie uitvoeren, maken we een spreidingsdiagram om de relatie tussen uren en examenscore te visualiseren:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size= 2 )

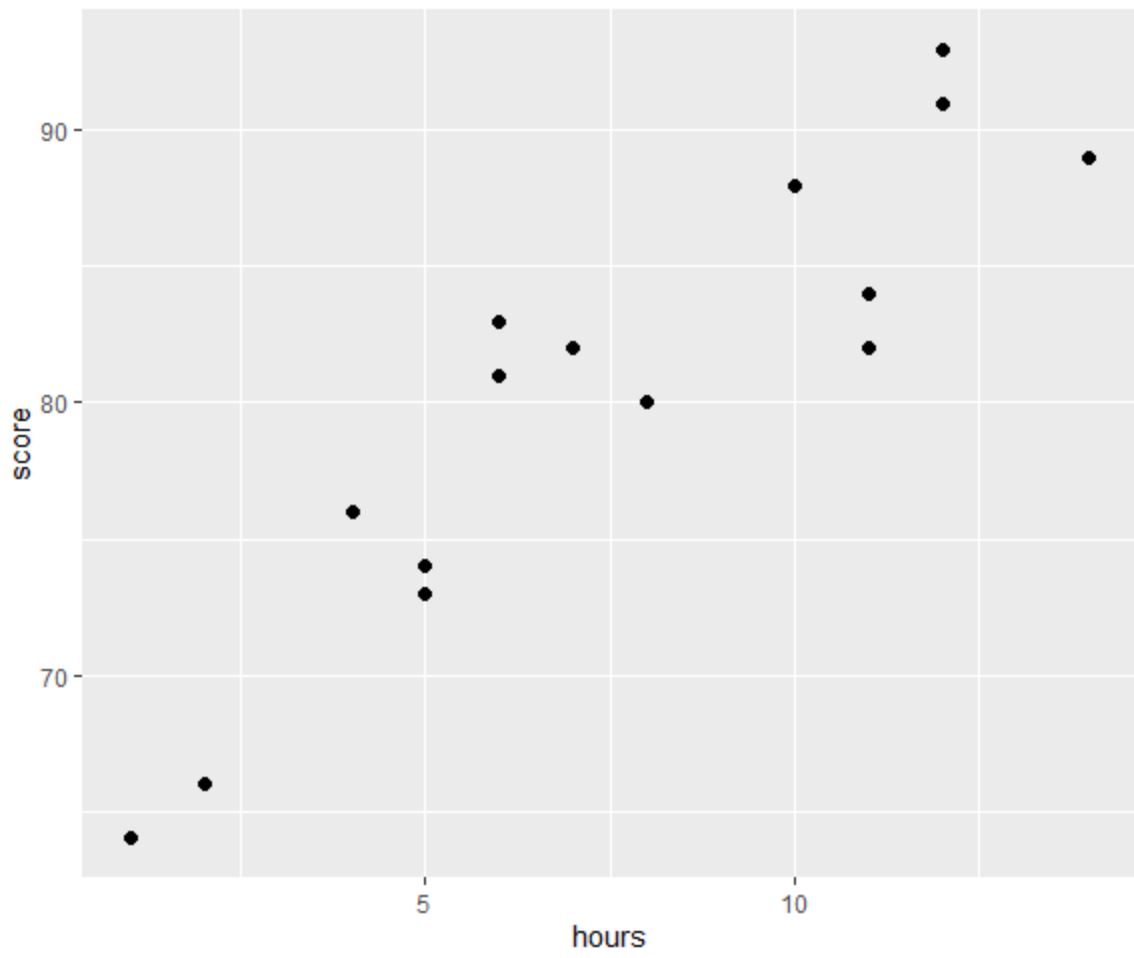
Een van de vier aannames van lineaire regressie is dat er een lineair verband bestaat tussen de voorspeller en de responsvariabele.

Uit de grafiek kunnen we zien dat de relatie lineair lijkt te zijn. Naarmate het aantal uren toeneemt, stijgt de score ook lineair.

Vervolgens kunnen we een boxplot maken om de verdeling van examenresultaten te visualiseren en te controleren op uitschieters.

Opmerking : R definieert een waarneming als een uitbijter als deze 1,5 keer de interkwartielafstand boven het derde kwartiel of 1,5 keer de interkwartielafstand onder het eerste kwartiel ligt.

Als een waarneming een uitbijter is, verschijnt er een kleine cirkel in de boxplot:

 library (ggplot2)

#create scatterplot
ggplot(df, aes(y=score)) +
  geom_boxplot() 

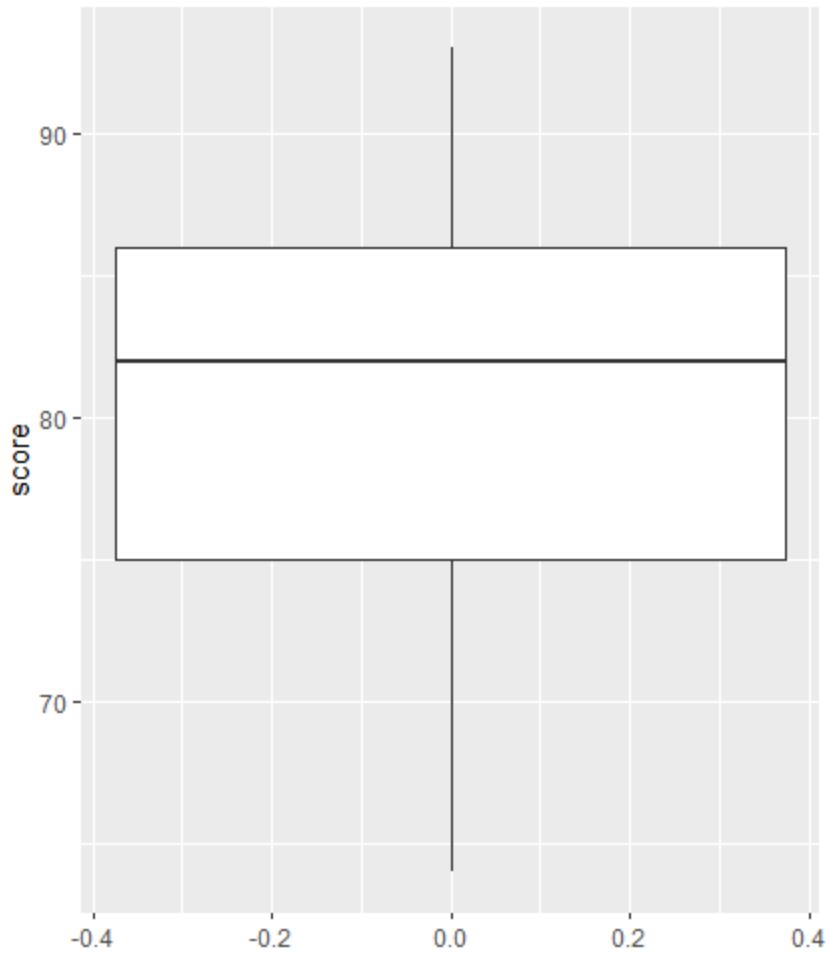
Er zijn geen kleine cirkels in de boxplot, wat betekent dat er geen uitschieters in onze dataset voorkomen.

Stap 3: Voer OLS-regressie uit

Vervolgens kunnen we de functie lm() in R gebruiken om een OLS-regressie uit te voeren, waarbij uren als voorspellende variabele en score als responsvariabele worden gebruikt:

 #fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Uit de samenvatting van het model kunnen we zien dat de aangepaste regressievergelijking is:

Score = 65.334 + 1.982*(uur)

Dit betekent dat elk extra bestudeerd uur gepaard gaat met een gemiddelde stijging van de examenscore van 1.982 punten.

De oorspronkelijke waarde van 65.334 vertelt ons de gemiddelde verwachte examenscore voor een student die nul uur studeert.

We kunnen deze vergelijking ook gebruiken om de verwachte examenscore te vinden op basis van het aantal uren dat een student studeert.

Een student die bijvoorbeeld 10 uur studeert, moet een examenscore van 85,15 behalen:

Score = 65,334 + 1,982*(10) = 85,15

Zo interpreteert u de rest van de modelsamenvatting:

• Pr(>|t|): Dit is de p-waarde die is gekoppeld aan de modelcoëfficiënten. Omdat de p-waarde voor uren (2.25e-06) aanzienlijk kleiner is dan 0,05, kunnen we zeggen dat er een statistisch significant verband bestaat tussen uren en score .
• Meerdere R-kwadraat: Dit getal vertelt ons dat het percentage variatie in examenscores kan worden verklaard door het aantal bestudeerde uren. Over het algemeen geldt dat hoe groter de R-kwadraatwaarde van een regressiemodel is, hoe beter de voorspellende variabelen de waarde van de responsvariabele kunnen voorspellen. In dit geval kan 83,1% van de variatie in scores worden verklaard door bestudeerde uren.
• Residuele standaardfout: dit is de gemiddelde afstand tussen de waargenomen waarden en de regressielijn. Hoe lager deze waarde, hoe beter een regressielijn kan corresponderen met de waargenomen gegevens. In dit geval wijkt de gemiddelde score op het examen 3.641 punten af van de score voorspeld door de regressielijn.
• F-statistiek en p-waarde: De F-statistiek ( 63.91 ) en de bijbehorende p-waarde ( 2.253e-06 ) vertellen ons de algehele betekenis van het regressiemodel, dat wil zeggen of de voorspellende variabelen in het model nuttig zijn om de variatie te verklaren . in de responsvariabele. Omdat de p-waarde in dit voorbeeld kleiner is dan 0,05, is ons model statistisch significant en worden uren als nuttig beschouwd bij het verklaren van de scorevariatie .

Stap 4: Maak resterende plots

Ten slotte moeten we residuele plots maken om de aannames van homoscedasticiteit en normaliteit te controleren.

De aanname van homoscedasticiteit is dat de residuen van een regressiemodel ongeveer gelijke variantie hebben op elk niveau van een voorspellende variabele.

Om te verifiëren dat aan deze veronderstelling is voldaan, kunnen we een grafiek van residuen versus passingen maken.

Op de x-as worden de gefitte waarden weergegeven en op de y-as de residuen. Zolang de residuen willekeurig en uniform verspreid lijken te zijn over de grafiek rond de nulwaarde, kunnen we aannemen dat de homoscedasticiteit niet wordt geschonden:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

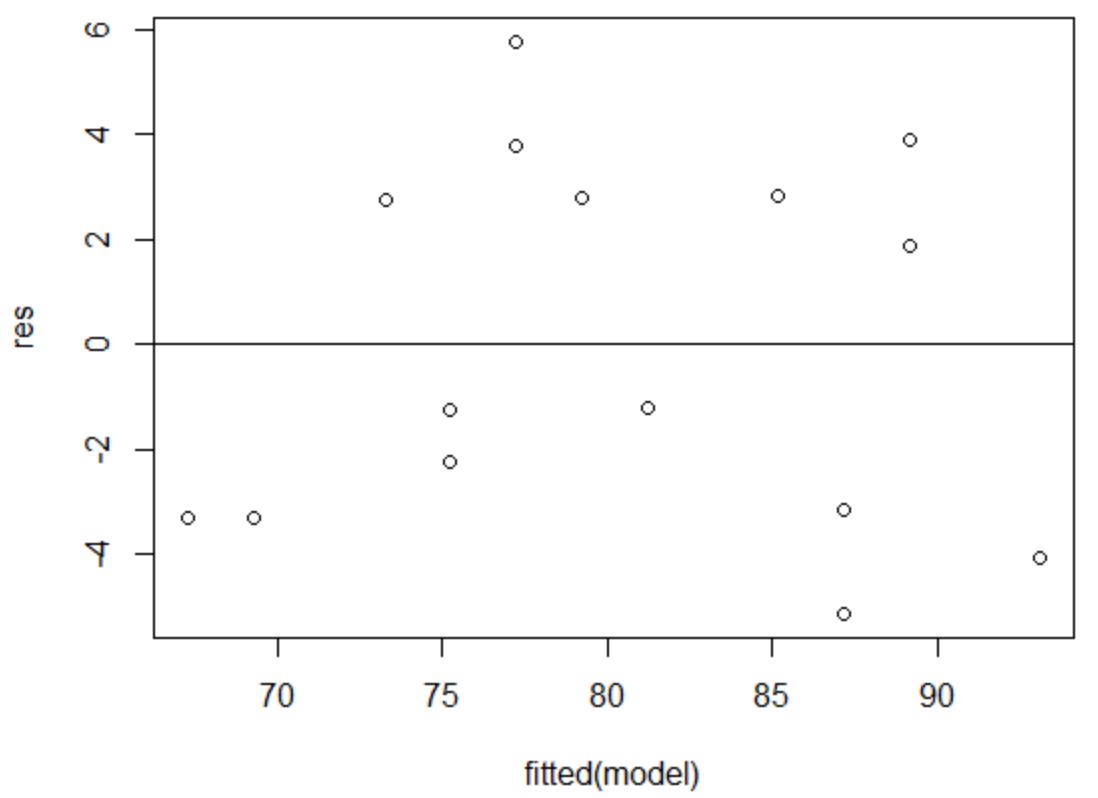
De residuen lijken willekeurig rond nul verspreid te zijn en vertonen geen merkbaar patroon, dus aan deze veronderstelling wordt voldaan.

De normaliteitsaanname stelt dat de residuen van een regressiemodel bij benadering normaal verdeeld zijn.

Om te controleren of aan deze veronderstelling is voldaan, kunnen we een QQ-plot maken. Als de plotpunten langs een ruwweg rechte lijn liggen die een hoek van 45 graden vormt, zijn de gegevens normaal verdeeld:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

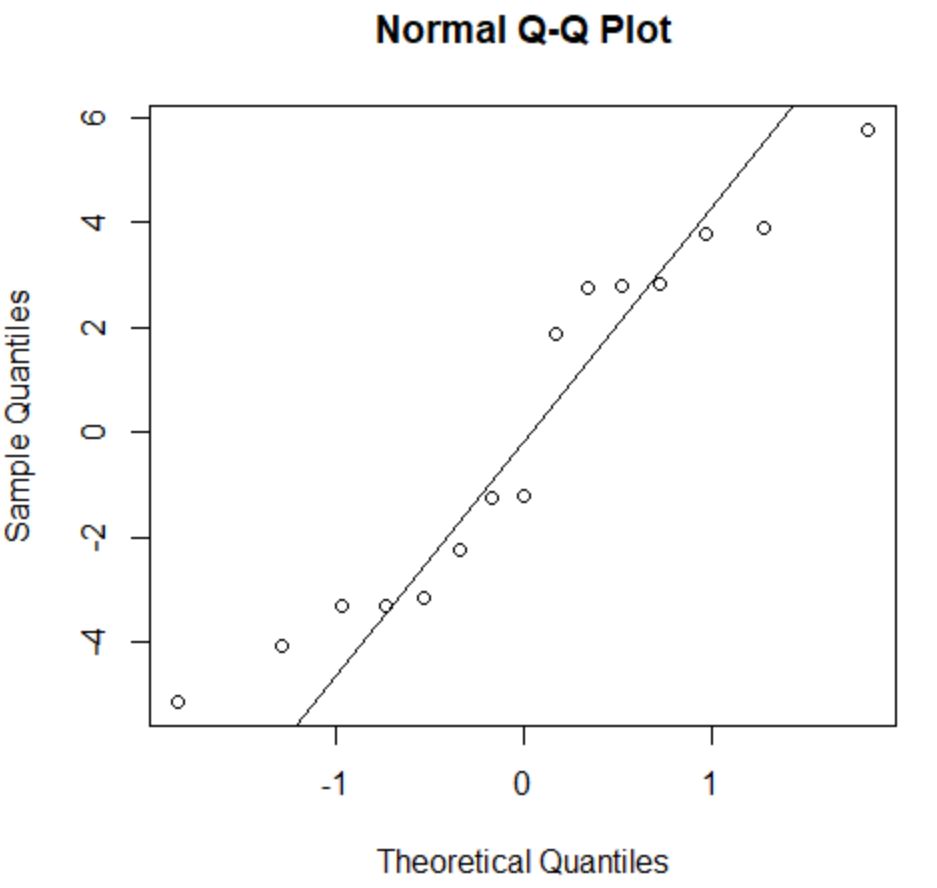
De residuen wijken een beetje af van de 45 graden-lijn, maar niet genoeg om ernstige zorgen te veroorzaken. We kunnen ervan uitgaan dat aan de normaliteitsaanname is voldaan.

Omdat de residuen normaal verdeeld en homoskedastisch zijn, hebben we geverifieerd dat aan de aannames van het OLS-regressiemodel is voldaan.

De output van ons model is dus betrouwbaar.

Opmerking : als aan een of meer van de aannames niet wordt voldaan, kunnen we proberen onze gegevens te transformeren .

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in R kunt uitvoeren:

Hoe meervoudige lineaire regressie uit te voeren in R
Hoe exponentiële regressie uit te voeren in R
Hoe u een gewogen kleinste kwadratenregressie uitvoert in R