Ols-regressie uitvoeren in python (met voorbeeld)

Gewone kleinste kwadratenregressie (OLS) is een methode waarmee we een lijn kunnen vinden die het beste de relatie beschrijft tussen een of meer voorspellende variabelen en eenresponsvariabele .

Met deze methode kunnen we de volgende vergelijking vinden:

ŷ = _b0 + _b1 x

Goud:

• ŷ : De geschatte responswaarde
• b ₀ : De oorsprong van de regressielijn
• b ₁ : De helling van de regressielijn

Deze vergelijking kan ons helpen de relatie tussen de voorspeller en de responsvariabele te begrijpen, en kan worden gebruikt om de waarde van een responsvariabele te voorspellen gegeven de waarde van de voorspellende variabele.

In het volgende stapsgewijze voorbeeld ziet u hoe u OLS-regressie in Python uitvoert.

Stap 1: Creëer de gegevens

Voor dit voorbeeld maken we een dataset met de volgende twee variabelen voor 15 studenten:

• Totaal aantal bestudeerde uren
• Examenresultaat

We voeren een OLS-regressie uit, waarbij we uren gebruiken als voorspellende variabele en examenscore als responsvariabele.

De volgende code laat zien hoe u deze nep-dataset in panda’s kunt maken:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Stap 2: Voer een OLS-regressie uit

Vervolgens kunnen we de functies in de statsmodels- module gebruiken om een OLS-regressie uit te voeren, waarbij uren als voorspellende variabele en score als responsvariabele worden gebruikt:

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Uit de coef- kolom kunnen we de regressiecoëfficiënten zien en de volgende aangepaste regressievergelijking schrijven:

Score = 65.334 + 1.9824*(uren)

Dit betekent dat elk extra bestudeerd uur gepaard gaat met een gemiddelde stijging van de examenscore van 1,9824 punten.

De oorspronkelijke waarde van 65.334 vertelt ons de gemiddelde verwachte examenscore voor een student die nul uur studeert.

We kunnen deze vergelijking ook gebruiken om de verwachte examenscore te vinden op basis van het aantal uren dat een student studeert.

Een student die bijvoorbeeld 10 uur studeert, moet een examenscore van 85,158 behalen:

Score = 65,334 + 1,9824*(10) = 85,158

Zo interpreteert u de rest van de modelsamenvatting:

• P(>|t|): Dit is de p-waarde die is gekoppeld aan de modelcoëfficiënten. Omdat de p-waarde voor uren (0,000) kleiner is dan 0,05, kunnen we zeggen dat er een statistisch significant verband bestaat tussen uren en score .
• R-kwadraat: Dit vertelt ons dat het percentage variatie in examenscores kan worden verklaard door het aantal gestudeerde uren. In dit geval kan 83,1% van de variatie in scores worden verklaard door bestudeerde uren.
• F-statistiek en p-waarde: De F-statistiek ( 63.91 ) en de bijbehorende p-waarde ( 2.25e-06 ) vertellen ons de algehele betekenis van het regressiemodel, dwz of de voorspellende variabelen in het model nuttig zijn bij het verklaren van variatie. in de responsvariabele. Omdat de p-waarde in dit voorbeeld kleiner is dan 0,05, is ons model statistisch significant en worden uren als nuttig beschouwd bij het verklaren van de scorevariatie .

Stap 3: Visualiseer de best passende lijn

Ten slotte kunnen we het datavisualisatiepakket matplotlib gebruiken om de regressielijn te visualiseren die is aangepast aan de feitelijke gegevenspunten:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

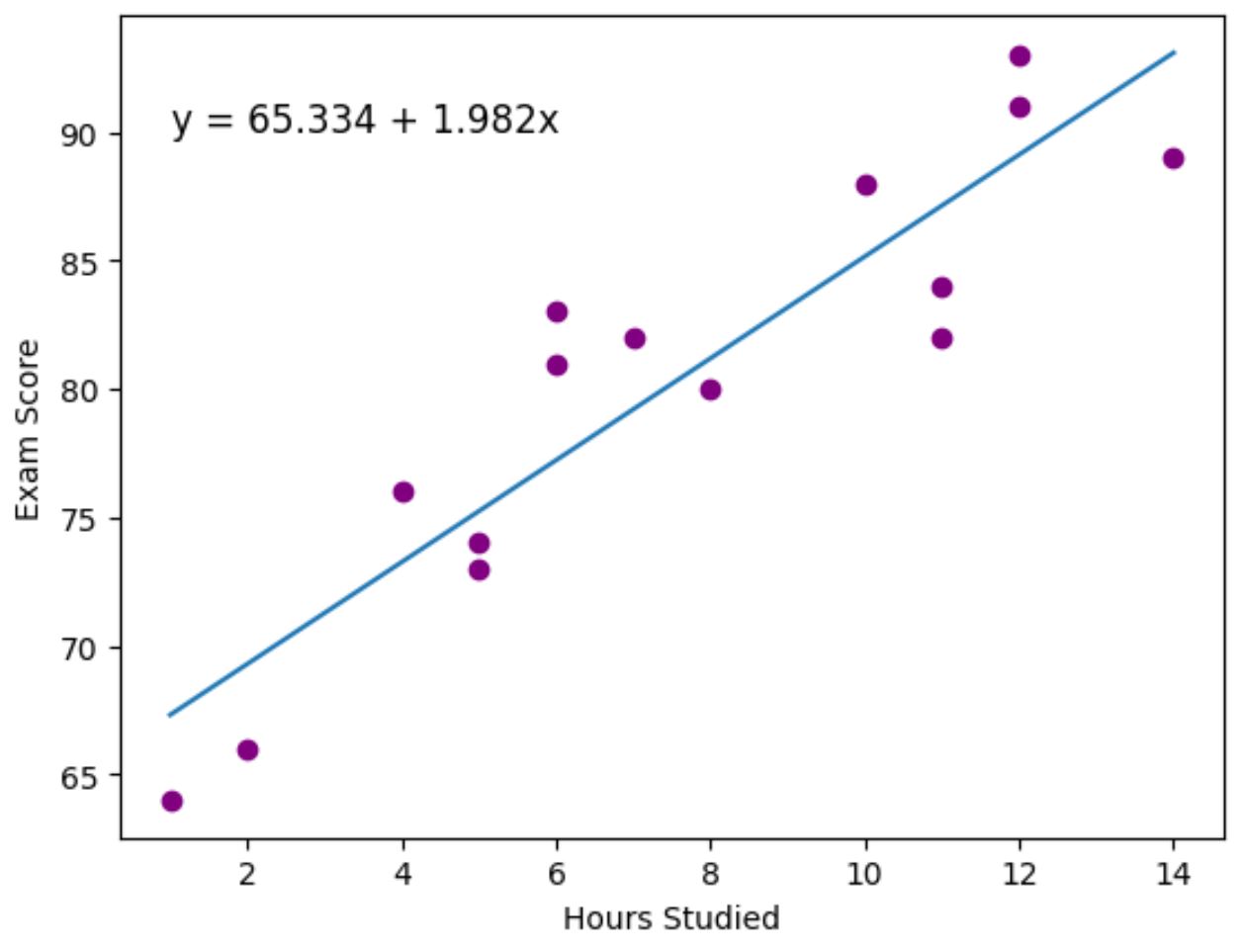
De paarse stippen vertegenwoordigen de werkelijke gegevenspunten en de blauwe lijn vertegenwoordigt de aangepaste regressielijn.

We hebben ook de functie plt.text() gebruikt om de aangepaste regressievergelijking aan de linkerbovenhoek van de plot toe te voegen.

Als we naar de grafiek kijken, lijkt het erop dat de aangepaste regressielijn de relatie tussen de urenvariabele en de scorevariabele vrij goed weergeeft.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in Python kunt uitvoeren:

Hoe logistieke regressie uit te voeren in Python
Exponentiële regressie uitvoeren in Python
Hoe AIC van regressiemodellen in Python te berekenen