Inverse normale verdeling: definitie en voorbeeld

De term inverse normale verdeling verwijst naar de methode waarbij een bekende waarschijnlijkheid wordt gebruikt om de overeenkomstige z-kritische waarde in een normale verdeling te vinden.

Dit moet niet worden verward met de inverse Gauss-verdeling , die een continue kansverdeling is.

Deze tutorial biedt verschillende voorbeelden van het gebruik van de inverse normale verdeling in verschillende statistische software.

Inverse normale verdeling, we hebben een TI-83- of TI-84-rekenmachine

De kans is groot dat u de term ‚inverse normale verdeling‘ tegenkomt op een TI-83- of TI-84-rekenmachine, die de volgende functie gebruikt om de kritische z-waarde te vinden die overeenkomt met een bepaalde waarschijnlijkheid:

invNorm(waarschijnlijkheid, μ, σ)

Goud:

• waarschijnlijkheid: het significantieniveau
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

U kunt deze functie op een TI-84-rekenmachine openen door op 2nd en vervolgens op vars te drukken. Dit brengt u naar een DISTR- scherm waar u vervolgens invNorm() kunt gebruiken:

We kunnen deze functie bijvoorbeeld gebruiken om de z-kritische waarde te vinden die overeenkomt met een waarschijnlijkheidswaarde van 0,05:

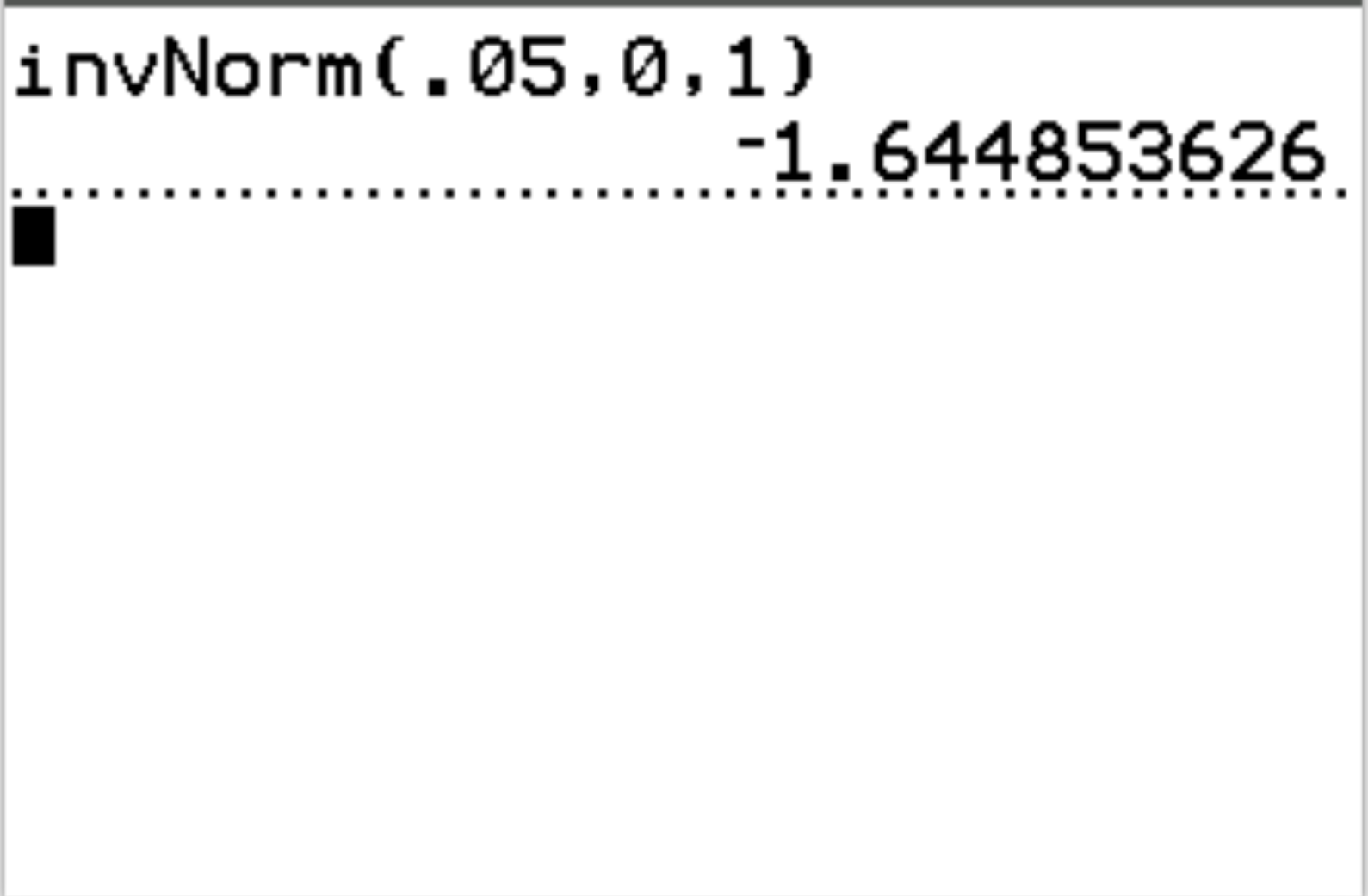
De kritische z-waarde die overeenkomt met een waarschijnlijkheidswaarde van 0,05 is -1,64485 .

Gerelateerd: InvNorm gebruiken op een TI-84-rekenmachine (met voorbeelden)

Inverse normale verdeling in Excel

Om de z-kritieke waarde te vinden die is gekoppeld aan een bepaalde waarschijnlijkheidswaarde in Excel, kunnen we de functie INVNORM() gebruiken, die de volgende syntaxis gebruikt:

INVNORM(p, gemiddelde, sd)

Goud:

• p: het significantieniveau
• gemiddelde: bevolkingsgemiddelde
• sd: standaarddeviatie van de populatie

We kunnen deze functie bijvoorbeeld gebruiken om de z-kritische waarde te vinden die overeenkomt met een waarschijnlijkheidswaarde van 0,05:

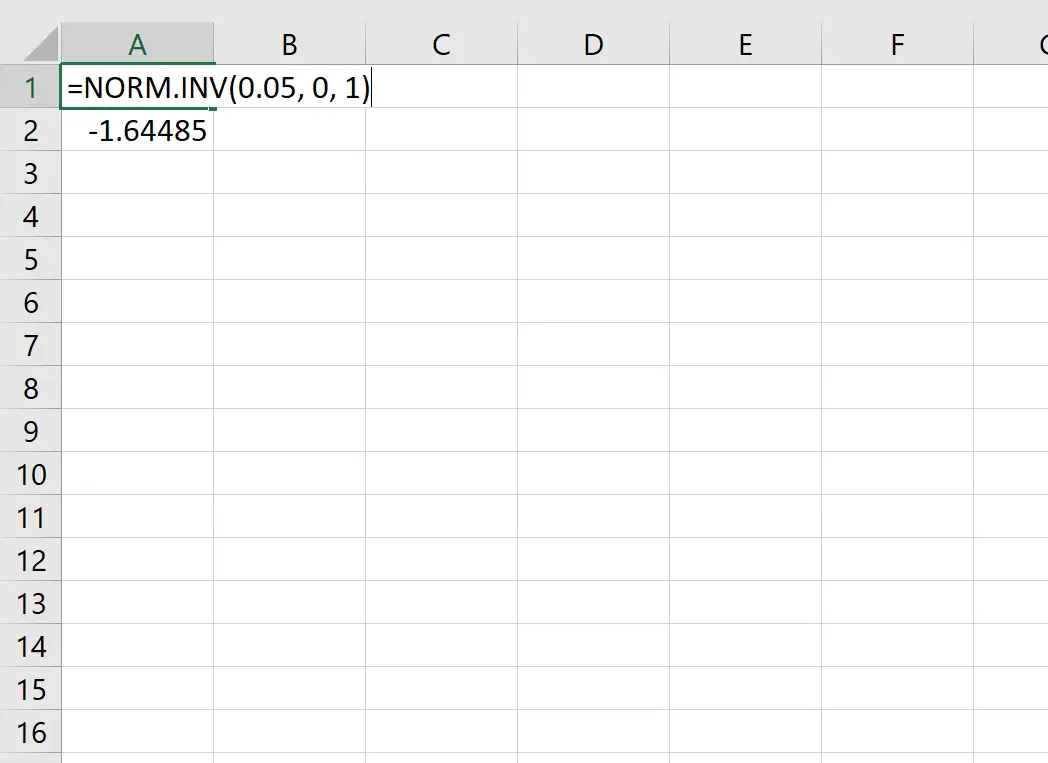
De kritische z-waarde die overeenkomt met een waarschijnlijkheidswaarde van 0,05 is -1,64485 .

Inverse normale verdeling in R

Om de z-kritische waarde te vinden die is gekoppeld aan een bepaalde waarschijnlijkheidswaarde in R, kunnen we de functie qnorm() gebruiken, die de volgende syntaxis gebruikt:

qnorm (p, gemiddelde, sd)

Goud:

• p: het significantieniveau
• gemiddelde: bevolkingsgemiddelde
• sd: standaarddeviatie van de populatie

We kunnen deze functie bijvoorbeeld gebruiken om de z-kritische waarde te vinden die overeenkomt met een waarschijnlijkheidswaarde van 0,05:

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

Opnieuw is de kritische z-waarde die overeenkomt met een waarschijnlijkheidswaarde van 0,05 -1,64485 .