Onafhankelijke variabele

In dit artikel wordt uitgelegd wat onafhankelijke variabelen zijn. Zo zul je de betekenis van een onafhankelijke variabele vinden in de wiskunde en de statistiek, en zul je ook verschillende voorbeelden van dit soort variabelen zien.

Wat is een onafhankelijke variabele?

Een onafhankelijke variabele is een variabele waarvan de waarde niet afhankelijk is van de waarde van een andere variabele. Integendeel, als een onafhankelijke variabele zijn waarde verandert, verandert hij de waarde van een afhankelijke variabele.

Wanneer u een onafhankelijke variabele plot, wordt deze meestal weergegeven door de letter x en op de x-as (horizontale as).

De tijdsduur dat u een woning huurt, is bijvoorbeeld een onafhankelijke variabele die van invloed is op de prijs die u betaalt. Omdat de huurduur kan worden bepaald en de waarde ervan de prijsafhankelijke variabele beïnvloedt, geldt: hoe langer de faciliteiten worden gebruikt, hoe meer ze moeten betalen.

Onafhankelijke variabelen kunnen ook verklarende variabelen, invoervariabelen of gemanipuleerde variabelen worden genoemd.

Voorbeelden van onafhankelijke variabelen

Nu we de definitie van een onafhankelijke variabele hebben gezien, gaan we nu naar verschillende voorbeelden van dit type variabele kijken om het concept beter te begrijpen.

• De tijd die wordt besteed aan studeren (onafhankelijke variabele) heeft invloed op de behaalde cijfers (afhankelijke variabele).
• De prijs van een product (onafhankelijke variabele) verandert het aantal mensen dat bereid is het product te kopen (afhankelijke variabele).
• Omgevingstemperatuur (onafhankelijke variabele) beïnvloedt het aantal bosbranden (afhankelijke variabele).
• Reclame voor een product (onafhankelijke variabele) heeft invloed op het aantal verkopen van dat product (afhankelijke variabele).
• Het aantal inwoners van een stad (onafhankelijke variabele) is gekoppeld aan het aantal taxi’s in een stad (afhankelijke variabele).

Onafhankelijke variabelen in de wiskunde

In de wiskunde wordt een oorzaak-gevolgrelatie gewoonlijk gemodelleerd met behulp van een onafhankelijke variabele en een afhankelijke variabele. Een functie definieert dus de wiskundige relatie die bestaat tussen de onafhankelijke variabele en de afhankelijke variabele.

Onafhankelijke variabelen worden meestal weergegeven met de letter x , terwijl de letter y wordt gebruikt voor afhankelijke variabelen.

De functie y=2x geeft bijvoorbeeld aan dat wanneer de onafhankelijke variabele x met één eenheid toeneemt, de afhankelijke variabele y twee keer zoveel toeneemt.

Voor meer informatie over wiskundige functies raden we u aan onze partnerwebsite function.xyz te bezoeken.

Onafhankelijke variabelen in statistieken

In werkelijkheid is het echter erg moeilijk om een relatie te vinden tussen twee variabelen die kunnen worden gedefinieerd door een exacte wiskundige functie, omdat soms dezelfde waarde van een onafhankelijke variabele resulteert in een andere waarde van de afhankelijke variabele.

Soms halen we door meer te studeren bijvoorbeeld een lager cijfer, of juist door minder te studeren een beter cijfer. Daarom is het aantal uren dat we aan studeren besteden niet de enige factor die van invloed is op het behaalde cijfer. Het kan ook variëren afhankelijk van de moeilijkheidsgraad van het examen of de moeilijkheidsgraad van het bestudeerde onderwerp.

Daarom worden er in de statistiek gewoonlijk veel experimenten uitgevoerd om te bepalen of er een verband bestaat tussen een onafhankelijke variabele en een afhankelijke variabele. De verkregen resultaten kunnen vervolgens grafisch worden weergegeven om te controleren of de variabelen met elkaar verbonden zijn en, zo ja, welk type relatie ze hebben (positief, negatief, lineair, exponentieel, enz.).

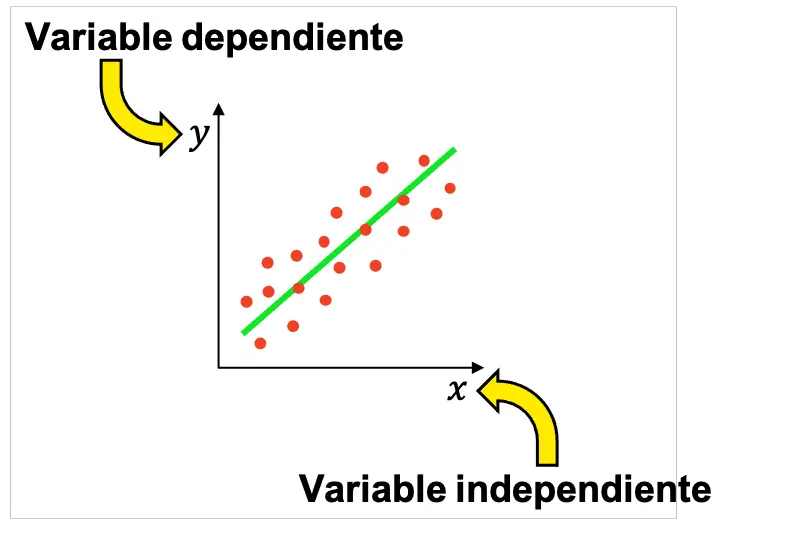
Houd er rekening mee dat er in een onderzoek meer dan één onafhankelijke variabele kan zijn, ook al worden de meest elementaire statistische onderzoeken uitgevoerd met één onafhankelijke en één afhankelijke variabele.

Nadat het statistische onderzoek is uitgevoerd, kan een wiskundige functie worden berekend die het mogelijk maakt een benadering te maken en zo de relatie tussen de variabelen te modelleren. Normaal gesproken maak je dus eerst een statistisch model en daarna een wiskundig model.