Eenrichtings-anova uitvoeren in excel

Een eenrichtings-ANOVA (“variantieanalyse”) wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

In deze zelfstudie wordt uitgelegd hoe u een eenrichtings-ANOVA uitvoert in Excel.

Voorbeeld: One-way ANOVA in Excel

Stel dat een onderzoeker 30 studenten recruteert om aan een onderzoek deel te nemen. Studenten worden willekeurig toegewezen om de komende drie weken een van de drie studietechnieken te gebruiken ter voorbereiding op een examen. Aan het einde van de drie weken maken alle studenten dezelfde toets.

De resultaten van de studententest worden hieronder weergegeven:

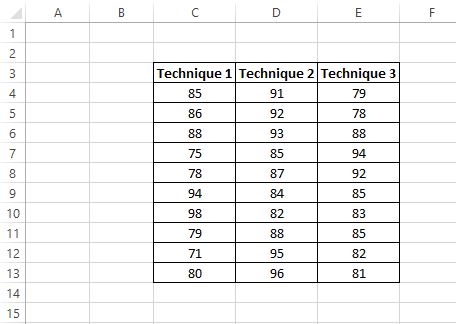
De onderzoeker wil een one-way ANOVA uitvoeren om te bepalen of de gemiddelde scores voor de drie groepen hetzelfde zijn.

Om eenrichtings-ANOVA in Excel uit te voeren, gaat u naar het tabblad Gegevens en klikt u vervolgens op de optie Gegevensanalyse in de groep Analyse .

Als u de optie Data Analysis niet ziet , moet u eerst de gratis Analysis ToolPak- software laden.

Zodra u erop klikt, verschijnt er een venster met verschillende scantoolopties. Selecteer Anova: Single Factor en klik vervolgens op OK .

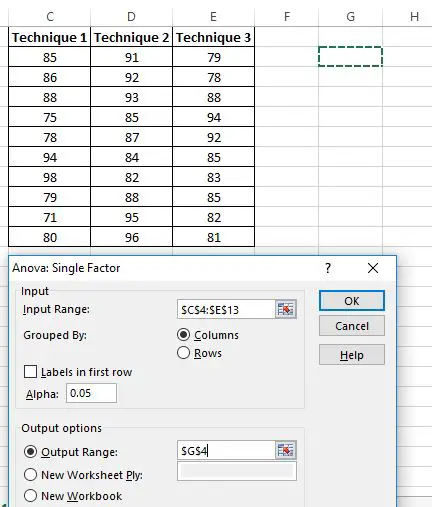
Er verschijnt een nieuw venster waarin om een invoerbereik wordt gevraagd. U kunt een kader rond uw gegevens slepen of het gegevensbereik handmatig invoeren. In dit geval bevinden onze gegevens zich in de cellen C4:E13 .

Kies vervolgens een alfaniveau voor de test. Standaard is dit getal 0,05. In dit geval laat ik het op 0,05 staan.

Kies ten slotte een cel voor het Uitvoerbereik , waar de eenrichtings-ANOVA-resultaten verschijnen. In dit geval kies ik cel G4 .

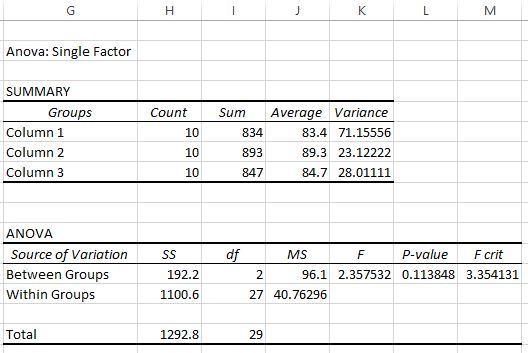
Zodra u op OK klikt, verschijnt het eenrichtings-ANOVA-resultaat:

Interpretatie van het resultaat

In de uitvoer worden twee tabellen weergegeven. De eerste is een samenvattende tabel die het aantal testscores in elke groep toont, de som van de testscores, het gemiddelde van de testscores en de variantie van de testscores.

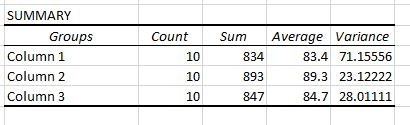
Bedenk dat een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer groepen.

Uit deze eerste tabel kunnen we zien dat de gemiddelde score voor elk van de drie groepen verschillend is, maar om te weten of deze verschillen statistisch significant zijn, moeten we naar de tweede tabel kijken.

De tweede tabel toont de F-teststatistiek, de kritische F-waarde en de p-waarde:

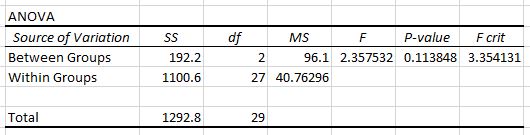
In dit geval is de F-teststatistiek 2,3575 en is de kritische waarde van F 3,3541 . Omdat de F-teststatistiek kleiner is dan de kritische waarde van F, hebben we niet voldoende bewijs om de nulhypothese te verwerpen dat de gemiddelden van de drie groepen gelijk zijn.

Dit betekent dat we onvoldoende bewijs hebben om te zeggen dat er een verschil is in testresultaten tussen de drie onderzoekstechnieken.

We zouden ook de p-waarde kunnen gebruiken om tot dezelfde conclusie te komen. In dit geval is de p-waarde 0,1138 , wat hoger is dan het alfaniveau van 0,05 .

Dit betekent dat we niet voldoende bewijs hebben om de nulhypothese te verwerpen dat de gemiddelden van de drie groepen gelijk zijn.

Opmerking: in gevallen waarin u de nulhypothese verwerpt, kunt u een post-hoctest van Tukey-Kramer uitvoeren om precies te bepalen welke groepsgemiddelden verschillend zijn.