Eenrichtings-anova uitvoeren in stata

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Dit type test wordt eenrichtings- ANOVA genoemd omdat we de impact van een voorspellende variabele op een responsvariabele analyseren. Als we in plaats daarvan geïnteresseerd zouden zijn in de impact van twee voorspellende variabelen op een responsvariabele, zouden we een tweerichtings- ANOVA kunnen uitvoeren.

In deze tutorial wordt uitgelegd hoe u een one-way ANOVA uitvoert in Stata.

Voorbeeld: One-way ANOVA in Stata

In dit voorbeeld gebruiken we de ingebouwde Stata-gegevensset, systolisch genaamd, om een eenrichtings-ANOVA uit te voeren. Deze dataset bevat de volgende drie variabelen voor 58 verschillende individuen:

• Medicijn gebruikt
• Patiënt ziekte
• Verandering in de systolische bloeddruk

We zullen de volgende stappen gebruiken om een eenrichtings-ANOVA uit te voeren om te bepalen of het gebruikte type medicatie een significante impact heeft op de verandering in de systolische bloeddruk.

Stap 1: Gegevens laden.

Laad eerst de gegevens door webuse systolic in het opdrachtvenster te typen en op Enter te klikken.

Stap 2: Bekijk de onbewerkte gegevens.

Voordat we een eenrichtings-ANOVA uitvoeren, kijken we eerst naar de onbewerkte gegevens. Navigeer in de bovenste menubalk naar Gegevens > Gegevenseditor > Gegevenseditor (Bladeren) . Dit toont ons de feitelijke gegevens voor alle 58 patiënten:

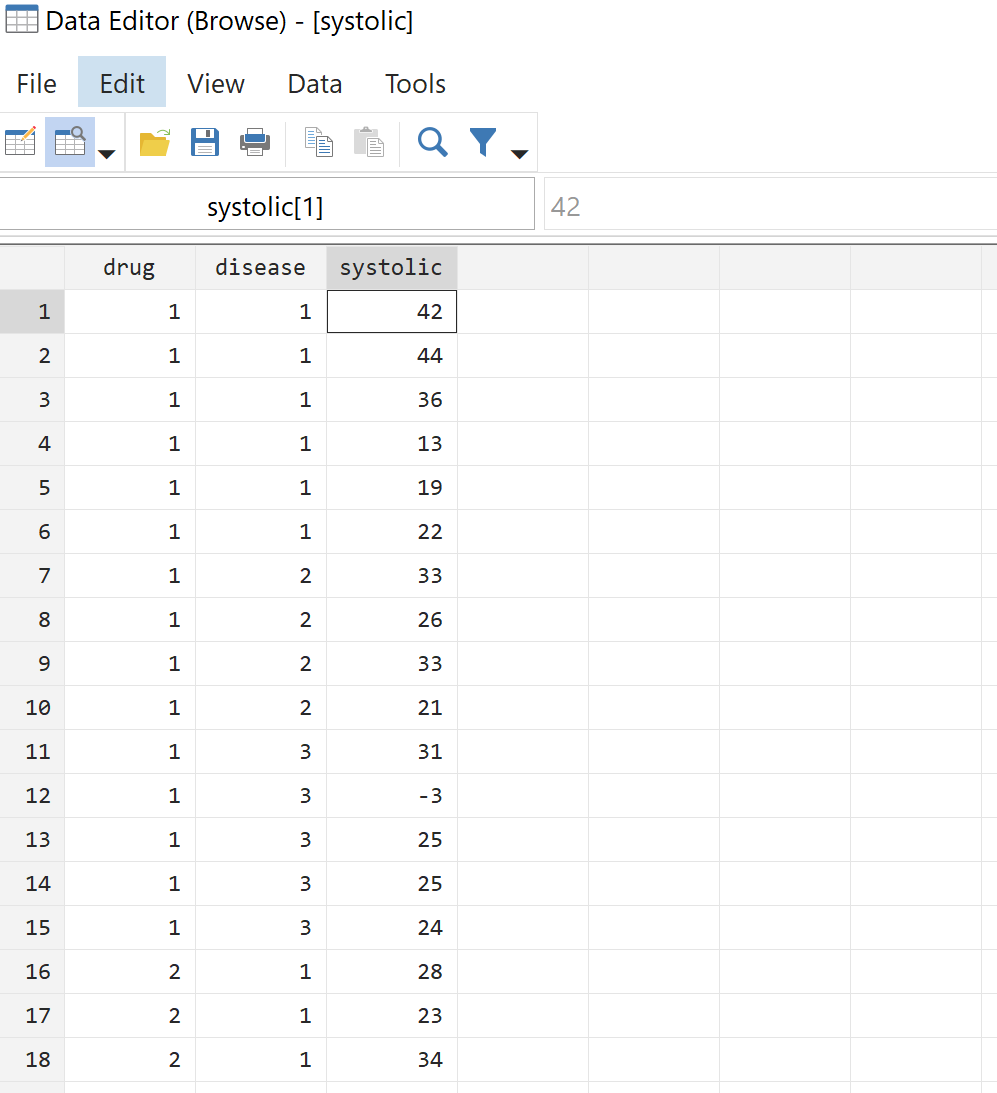
Stap 3: Visualiseer de gegevens.

Laten we vervolgens de gegevens visualiseren. We zullen boxplots maken om de verdeling van de systolische bloeddrukwaarden voor elke medicijncategorie weer te geven.

Ga in de bovenste menubalk naar Grafieken > Boxplot . Kies onder variabelen Systolisch:

Kies vervolgens in de subkop Categorieën onder Groeperingsvariabele het medicijn:

Klik op OK . Er wordt automatisch een diagram met vier boxplots weergegeven:

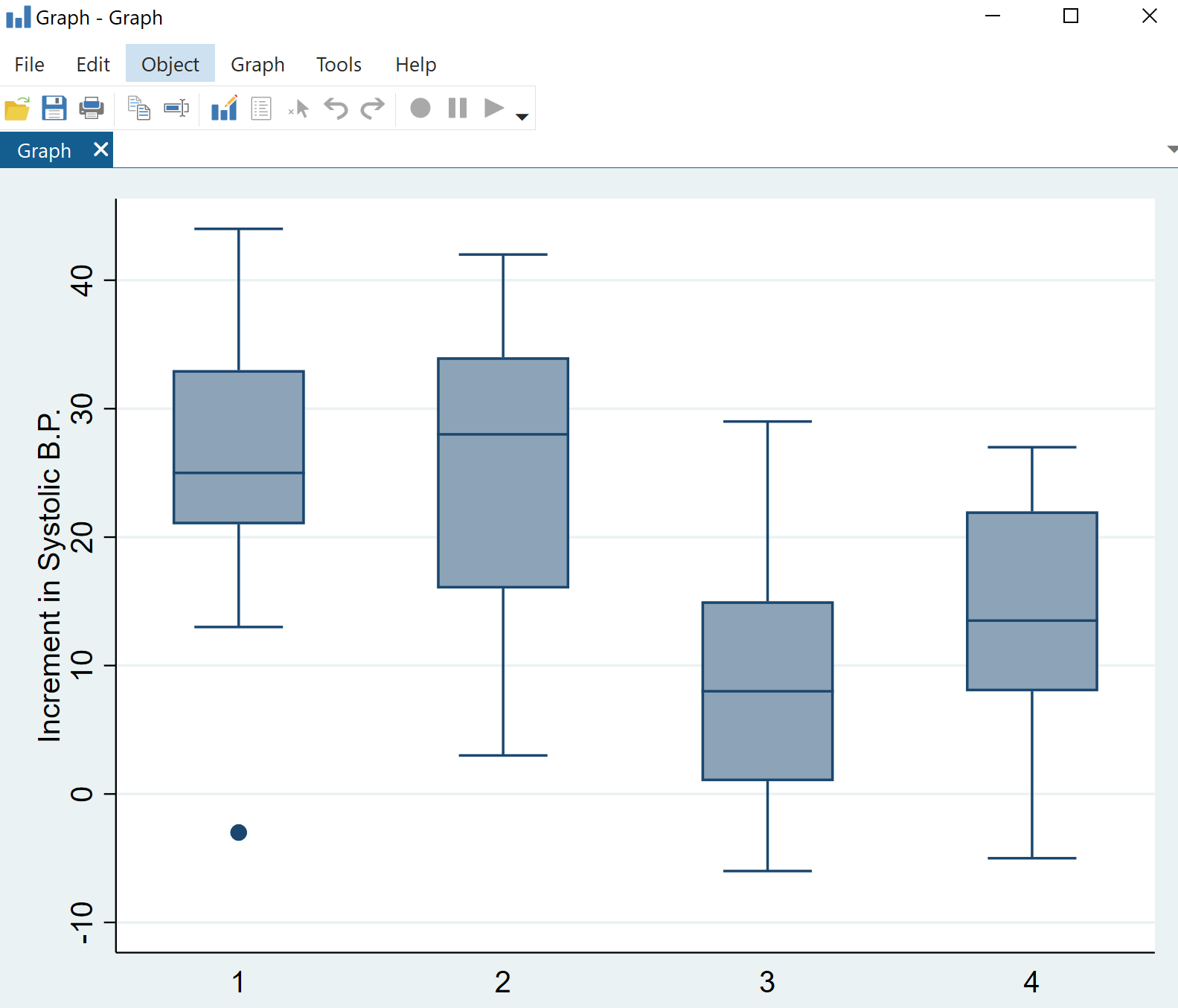
We kunnen meteen zien dat de verdeling van veranderingen in de systolische bloeddruk varieert tussen de categorieën geneesmiddelen, maar een eenrichtings-ANOVA zal ons vertellen of deze verschillen statistisch significant zijn.

Stap 4: Voer een eenrichtings-ANOVA uit.

Navigeer in de bovenste menubalk naar Statistieken > Lineaire en gerelateerde modellen > ANOVA/MANOVA > One-Way ANOVA .

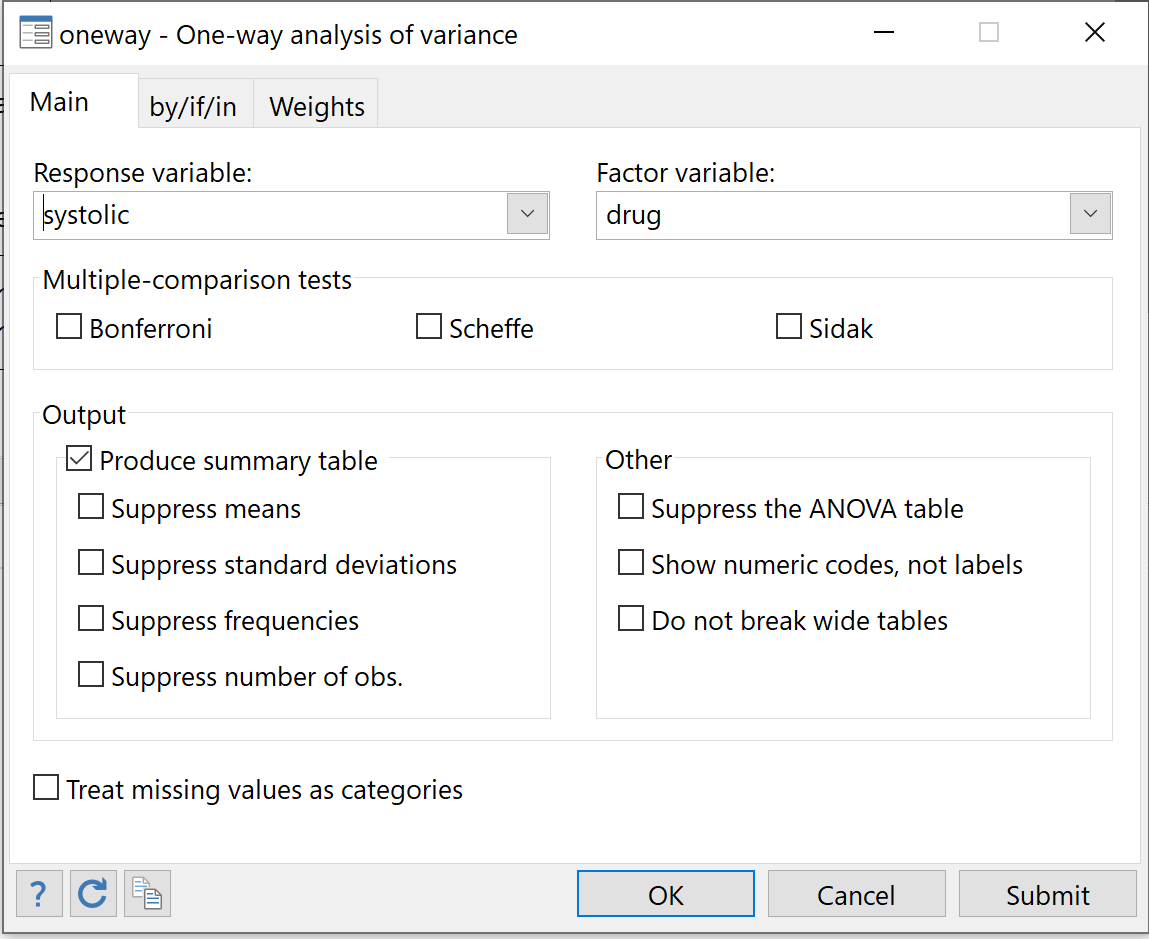
Kies onder Reactievariabele de optie Systolisch. Kies onder factorvariabele het medicijn. Klik vervolgens op het vakje naast Produceer een overzichtstabel , zodat we voor elke groep enkele beschrijvende basisstatistieken kunnen zien. Klik vervolgens op OK .

De volgende uitvoer wordt weergegeven:

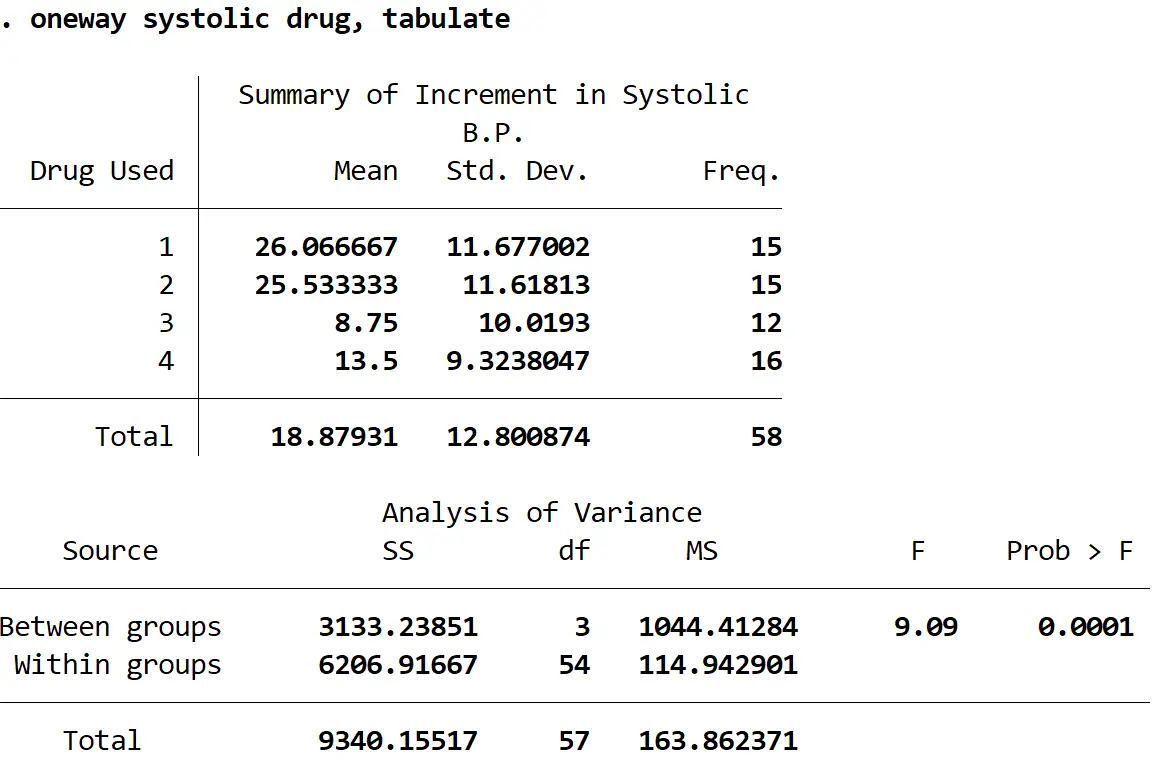
De F-statistiek is 9,09 en de overeenkomstige p-waarde is 0,0001 . Omdat de p-waarde kleiner is dan alfa = 0,05, kunnen we de nulhypothese verwerpen dat de gemiddelde verandering in de systolische bloeddruk voor elke groep gelijk is.

Met andere woorden: er is een statistisch significant verschil in de gemiddelde verandering in de systolische bloeddruk tussen ten minste twee medicijngroepen.

Stap 5: Voer meerdere vergelijkingstests uit.

Vervolgens kunnen we verschillende vergelijkingstests uitvoeren om erachter te komen welke groepsgemiddelden van elkaar verschillen.

Navigeer in de bovenste menubalk naar Statistieken > Samenvattingen, tabellen en tests > Samenvatting en beschrijvende statistieken > Paarsgewijze vergelijkingen van gemiddelden .

Kies bij Variabele de systolische responsvariabele. Kies bij Over de verklarende variabele medicijn . Kies voor Aanpassing voor meerdere vergelijkingen de Tukey-methode .

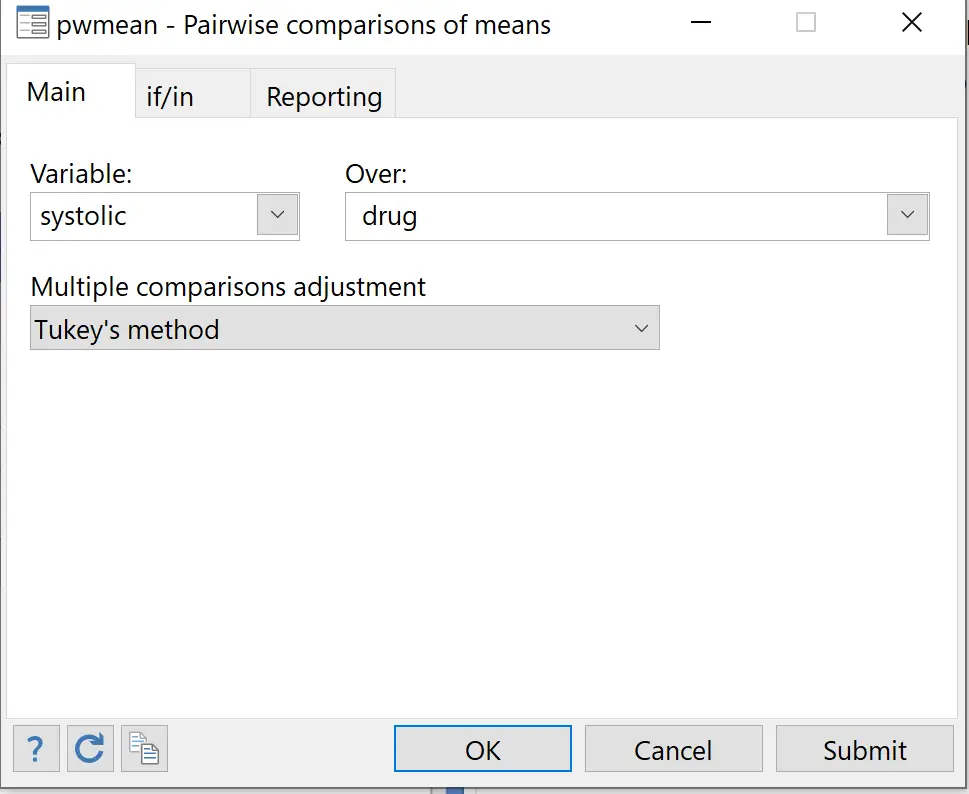
Klik vervolgens onder de subkop Rapportage op de knop naast Tabellen met effecten en vink het vakje aan naast Tabel met effecten weergeven met betrouwbaarheidsintervallen en p-waarden . Klik vervolgens op OK .

De volgende resultaten worden weergegeven:

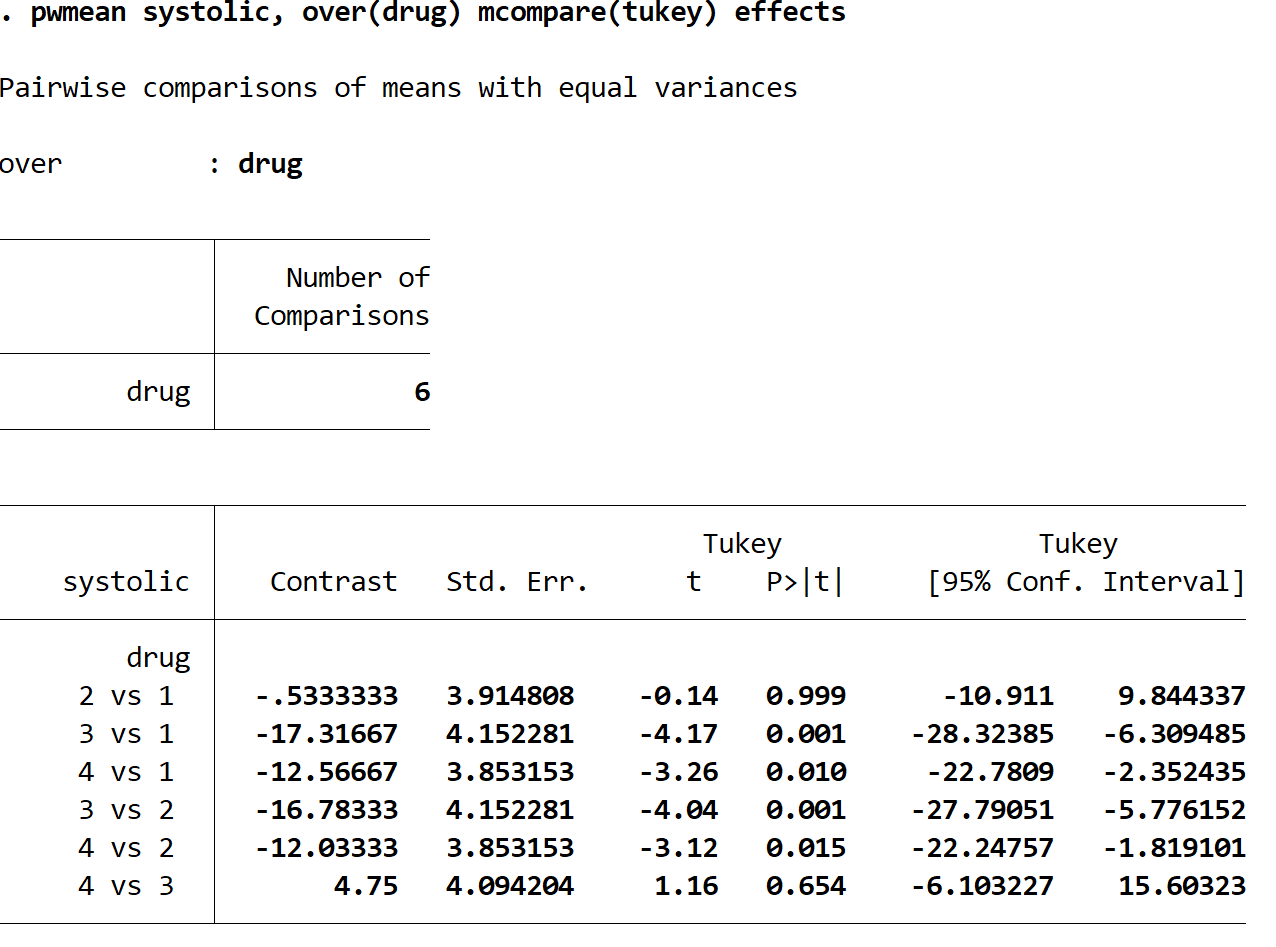
Elke rij vertegenwoordigt een vergelijking tussen twee specifieke medicijngroepen. In de eerste rij wordt bijvoorbeeld de gemiddelde verandering in de systolische bloeddruk tussen geneesmiddelgroep 2 en geneesmiddelgroep 1 vergeleken. De p-waarde voor deze vergelijking is 0,999 , wat extreem hoog is en niet minder dan 0,05. Dit betekent dat er geen statistisch significant verschil is tussen geneesmiddelgroepen 1 en 2.

We kunnen echter zien dat de p-waarden voor de volgende vergelijkingen allemaal kleiner zijn dan 0,05:

• geneeskunde 3 tot 1 | p-waarde = 0,001
• geneeskunde 4 tot 1 | p-waarde = 0,010
• medicijn 3 tegen 2 | p-waarde = 0,001
• medicijn 4 tegen 2 | p-waarde = 0,015

Dit betekent dat het verschil in gemiddelde verandering in systolische bloeddruk statistisch significant is tussen elk van deze groepen.

Stap 6: Rapporteer de resultaten.

Ten slotte zullen we de resultaten van onze eenrichtings-ANOVA-analyse rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een one-way ANOVA uitgevoerd om te bepalen of vier verschillende soorten medicijnen verschillende effecten hadden op de systolische bloeddruk.

De volgende tabel vat het aantal deelnemers in elke groep samen, evenals de gemiddelde verandering in de systolische bloeddruk en de standaardafwijking van de systolische bloeddruk voor elke groep:

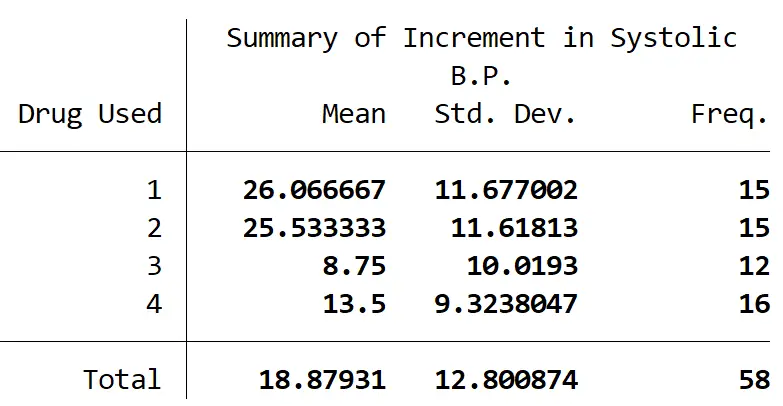
Uit een eenrichtings-ANOVA bleek dat er een statistisch significant verschil was tussen ten minste twee groepen (F(3, 54) = 9,09, p = 0,001).

Tukey’s test voor meerdere vergelijkingen onthulde dat de verandering in de systolische bloeddruk statistisch significant hoger was voor medicijn 3 dan voor medicijn 1 (17,32 +/- 4,15, p = 0,001), voor medicijn 3 vergeleken met medicijn 2 (16,78 +/- 4,15, p = 0,001), voor medicijn 4 vergeleken met medicijn 1 (12,57 +/- 3,85, p = 0,010), en voor medicijn 4 vergeleken met medicijn 2 (12,03 +/- 3,85, p = 0,015).

Er was geen statistisch significant verschil tussen geneesmiddelgroepen 1 en 2 (0,533 +/- 3,91, p = 0,999) of tussen geneesmiddelgroepen 3 en 4 (4,75 +/- 4,09, p = 0,654).