Wat is overfitting in machine learning? (uitleg & voorbeelden)

Bij machine learning bouwen we vaak modellen zodat we nauwkeurige voorspellingen kunnen doen over bepaalde fenomenen.

Stel dat we bijvoorbeeld een regressiemodel willen maken dat gebruikmaakt van de voorspellende variabele uren besteed aan studeren om de ACT-score van de responsvariabele voor middelbare scholieren te voorspellen.

Om dit model te bouwen, verzamelen we gegevens over de uren die aan studeren zijn besteed en de bijbehorende ACT-score voor honderden leerlingen in een bepaald schooldistrict.

Deze gegevens gaan we vervolgens gebruiken om een model te trainen dat voorspellingen kan doen over de score die een bepaalde leerling zal behalen op basis van het totaal aantal bestudeerde uren.

Om de bruikbaarheid van het model te beoordelen, kunnen we meten hoe goed de voorspellingen van het model overeenkomen met de waargenomen gegevens. Een van de meest gebruikte maatstaven om dit te doen is de gemiddelde kwadratische fout (MSE), die als volgt wordt berekend:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Goud:

• n: totaal aantal waarnemingen
• y _i : De responswaarde van de ^i-de waarneming
• f( _xi ): De voorspelde responswaarde van de i- ^de waarneming

Hoe dichter de modelvoorspellingen bij de waarnemingen liggen, hoe lager de MSE zal zijn.

Een van de grootste fouten die bij machinaal leren worden gemaakt, is echter het optimaliseren van modellen om de training MSE te verminderen, dat wil zeggen hoe goed de modelvoorspellingen overeenkomen met de gegevens die we hebben gebruikt om het model te trainen.

Wanneer een model zich te veel richt op het verminderen van de trainings-MSE, werkt het vaak te hard om patronen in de trainingsgegevens te vinden die eenvoudigweg door toeval worden veroorzaakt. Wanneer het model vervolgens wordt toegepast op onzichtbare gegevens, zijn de prestaties slecht.

Dit fenomeen staat bekend als overfitting . Dit gebeurt wanneer we een model te nauw ‘passen’ bij de trainingsgegevens en zo uiteindelijk een model bouwen dat niet bruikbaar is voor het doen van voorspellingen op basis van nieuwe gegevens.

Voorbeeld van overfitting

Om overfitting te begrijpen, gaan we terug naar het voorbeeld van het maken van een regressiemodel dat uren besteed aan studeren gebruikt om de ACT-score te voorspellen.

Laten we zeggen dat we gegevens verzamelen voor 100 leerlingen in een bepaald schooldistrict en een snelle spreidingsdiagram maken om de relatie tussen de twee variabelen te visualiseren:

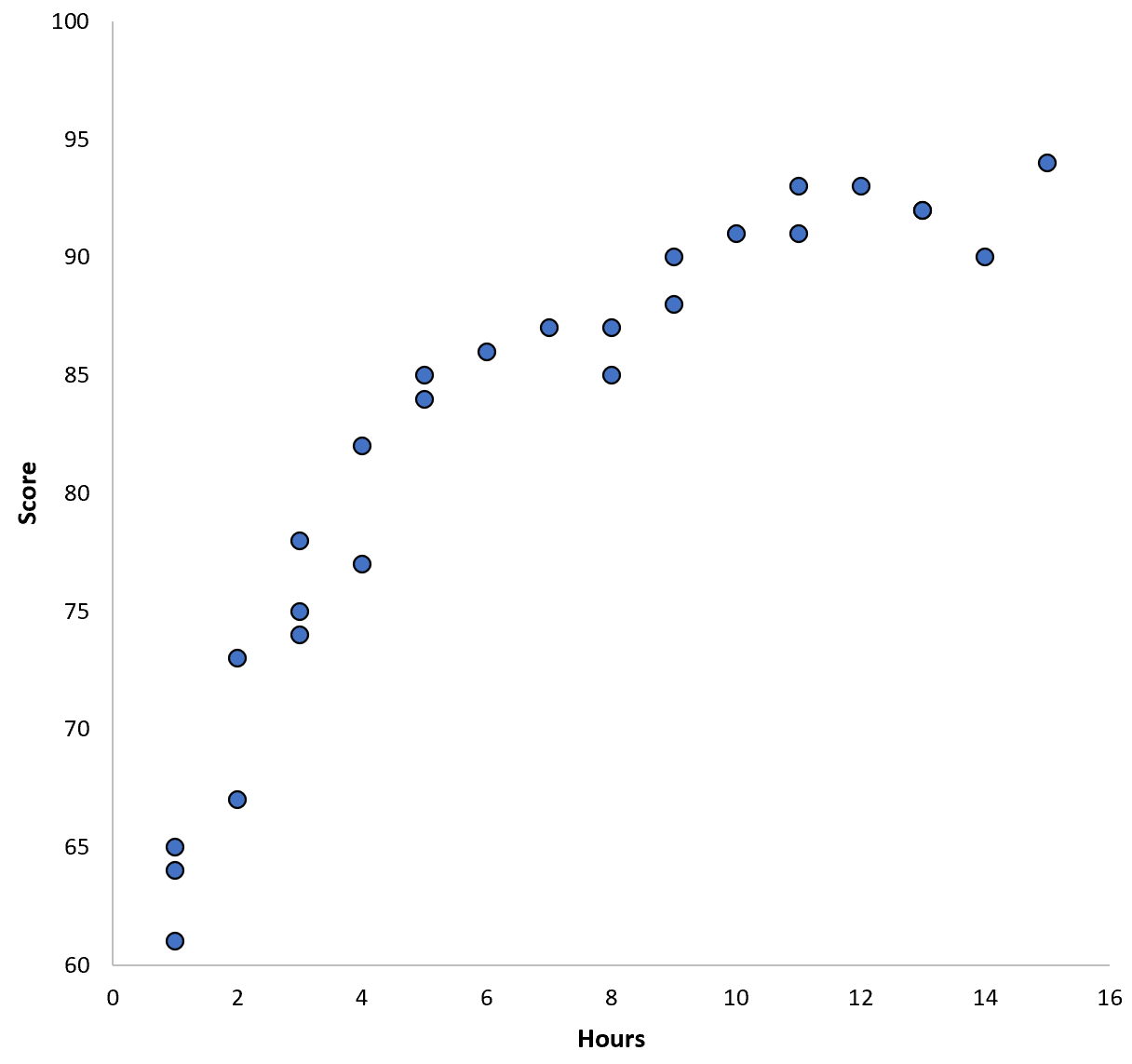
De relatie tussen de twee variabelen lijkt kwadratisch te zijn, dus stel dat we het volgende kwadratische regressiemodel toepassen:

Score = 60,1 + 5,4*(uren) – 0,2*(uren) ²

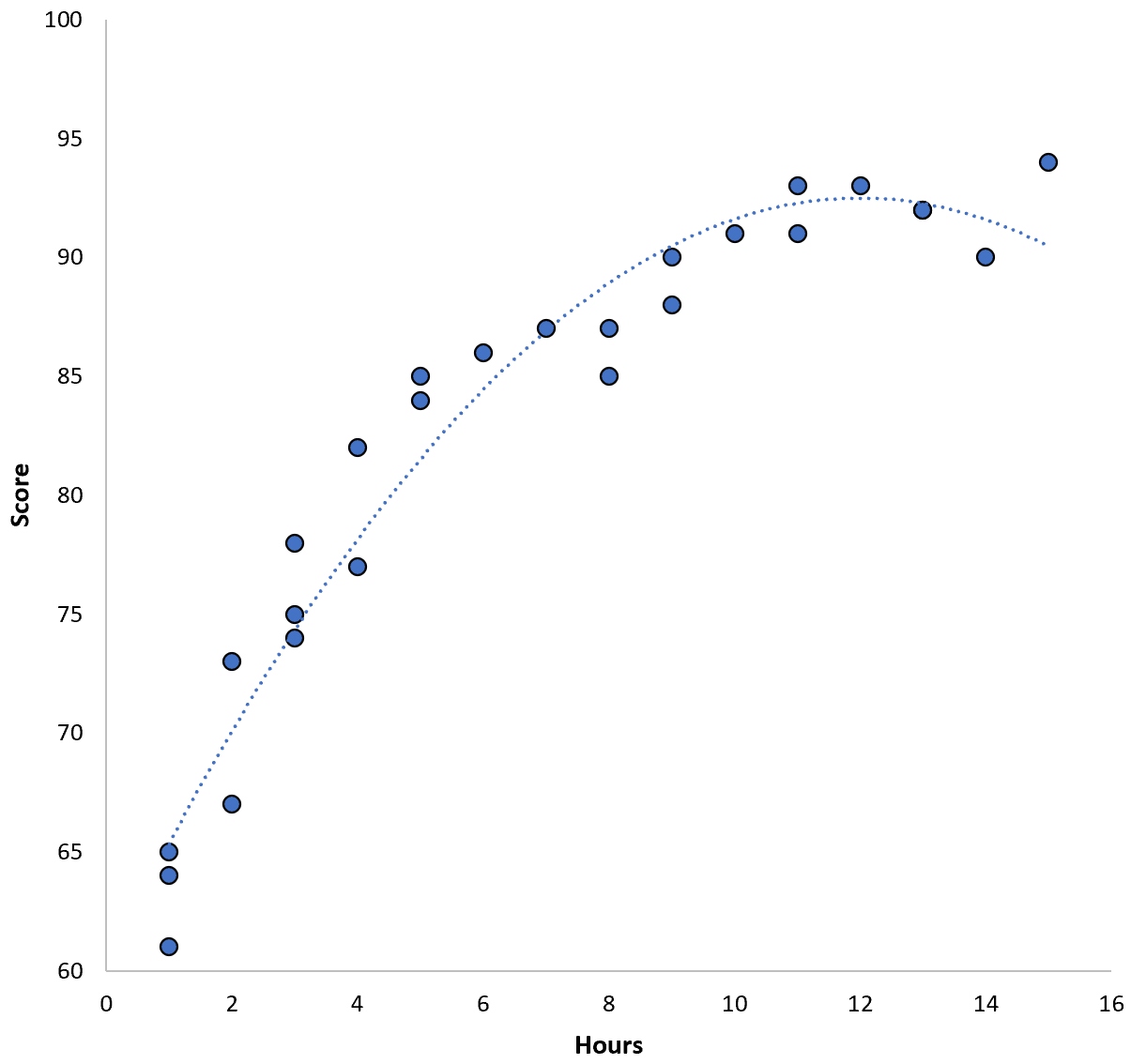
Dit model heeft een gemiddelde kwadratische fout (MSE) van 3,45 . Dat wil zeggen dat het wortelgemiddelde-kwadratenverschil tussen de voorspellingen van het model en de werkelijke ACT-scores 3,45 bedraagt.

We zouden deze training-MSE echter kunnen verminderen door een polynoommodel van hogere orde toe te passen. Stel dat we bijvoorbeeld het volgende model toepassen:

Score = 64,3 – 7,1*(Uren) + 8,1*(Uren) ² – 2,1*(Uren) ³ + 0,2*(Uren ^{) 4 – 0,1*(Uren) 5 +} 0,2(Uren) ⁶

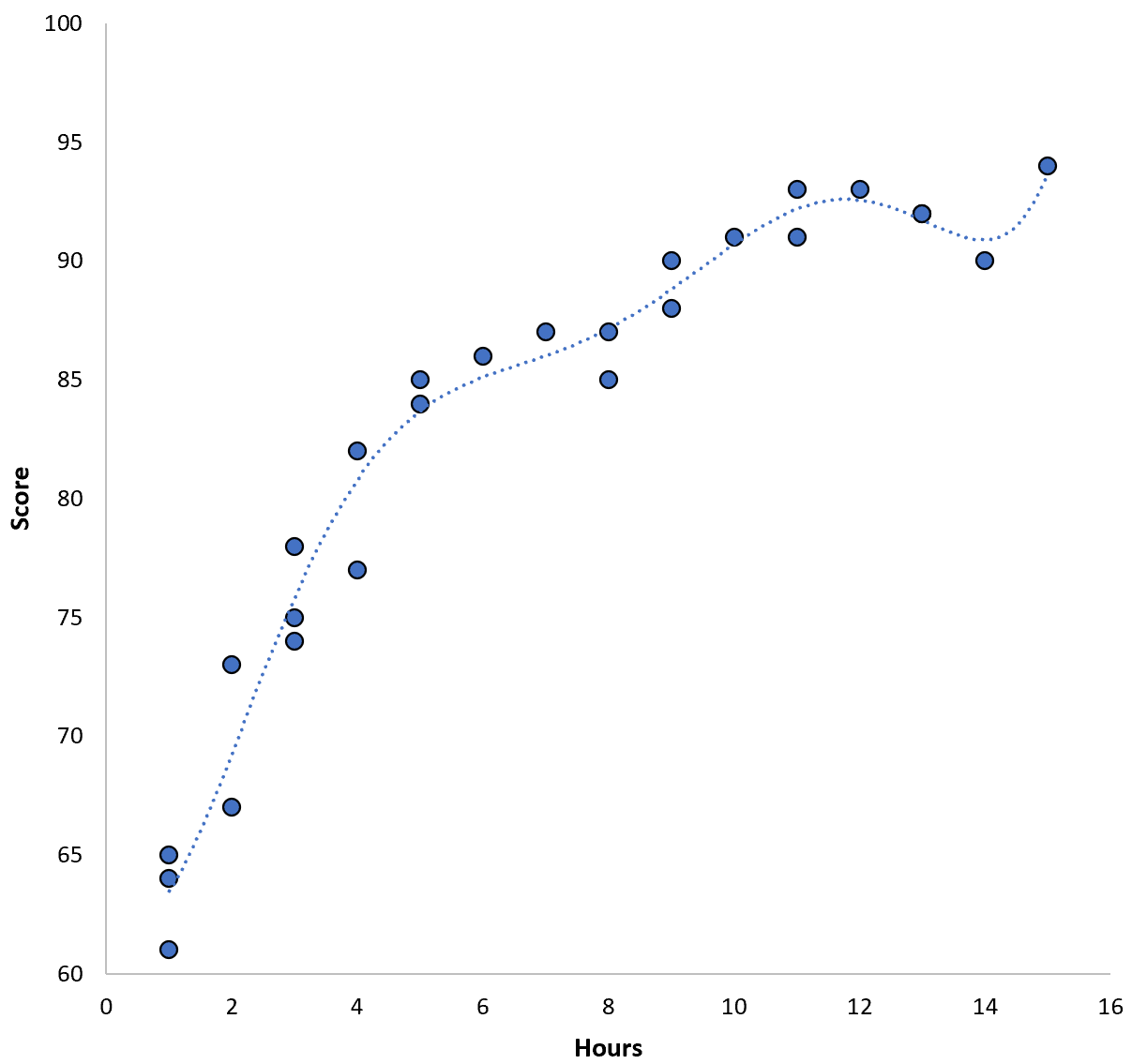
Merk op dat de regressielijn veel beter bij de werkelijke gegevens past dan de vorige regressielijn.

Dit model heeft een training root mean square error (MSE) van slechts 0,89 . Dat wil zeggen dat het kwadratische wortelverschil tussen de voorspellingen van het model en de werkelijke ACT-scores 0,89 bedraagt.

Deze MSE-training is veel kleiner dan die van het vorige model.

Het maakt ons echter niet zoveel uit hoe goed de voorspellingen van het model overeenkomen met de gegevens die we hebben gebruikt om het model te trainen. In plaats daarvan geven we vooral om de MSE-test – de MSE wanneer ons model wordt toegepast op onzichtbare gegevens.

Als we het bovenstaande polynomiale regressiemodel van hogere orde zouden toepassen op een onzichtbare dataset, zou het waarschijnlijk slechter presteren dan het eenvoudigere kwadratische regressiemodel. Dat wil zeggen, het zou een hogere MSE-test opleveren, en dat is precies wat we niet willen.

Hoe overfitting te detecteren en te voorkomen

De eenvoudigste manier om overfitting te detecteren is door kruisvalidatie uit te voeren. De meest gebruikte methode staat bekend als k-voudige kruisvalidatie en werkt als volgt:

Stap 1: Verdeel een dataset willekeurig in k groepen, of ‘vouwen’, van ongeveer gelijke grootte.

Stap 2: Kies een van de vouwen als uw holdingset. Pas de sjabloon aan de resterende k-1-vouwen aan. Bereken de MSE-proef op de waarnemingen in de gespannen lamel.

Stap 3: Herhaal dit proces k keer, telkens met een andere set als uitsluitingsset.

Stap 4: Bereken de totale MSE van de test als het gemiddelde van de k MSE’s van de test.

Test MSE = (1/k)*ΣMSE _i

Goud:

• k: Aantal vouwen
• MSE _i : Test MSE bij de ^i-de iteratie

Deze MSE-test geeft ons een goed beeld van hoe een bepaald model zal presteren op onbekende data.

In de praktijk kunnen we verschillende modellen passen en k-voudige kruisvalidatie uitvoeren op elk model om de MSE-test ervan te achterhalen. We kunnen dan het model met de laagste MSE-test kiezen als het beste model om voorspellingen in de toekomst te doen.

Dit zorgt ervoor dat we een model selecteren dat waarschijnlijk het beste presteert op basis van toekomstige gegevens, in tegenstelling tot een model dat simpelweg de training MSE minimaliseert en goed ‘past’ bij historische gegevens.

Aanvullende bronnen

Wat is de afweging tussen bias en variantie bij machinaal leren?
Een inleiding tot K-fold kruisvalidatie
Regressie- en classificatiemodellen in machine learning