Hoe u p-waarden kunt vinden in google spreadsheets (stap voor stap)

De eenvoudigste manier om p-waarden in Google Spreadsheets te berekenen is door de functie T.TEST() te gebruiken, die de p-waarde vindt die aan een t-test is gekoppeld en de volgende syntaxis gebruikt:

T.TEST (bereik 1, bereik 2, staarten, type)

Goud:

• bereik1: het eerste gegevensvoorbeeld
• bereik2: het tweede gegevensvoorbeeld
• staarten: het aantal staarten dat voor de test moet worden gebruikt
  • 1: Eenzijdige (of “eenzijdige”) t-test
  • 2: Tweezijdige (of “tweezijdige) t-test
• type: het type t-toets
  • 1: Gepaarde t-test
  • 2: T-test met twee steekproeven met gelijke variantie
  • 3: T-test met twee steekproeven met ongelijke variantie

Deze functie retourneert de p-waarde die overeenkomt met de t-test.

Het volgende stap-voor-stap voorbeeld laat zien hoe u deze functie in de praktijk kunt gebruiken.

Stap 1: Creëer de gegevens

Laten we eerst een nep-dataset maken met de hoogte van twee verschillende plantensoorten:

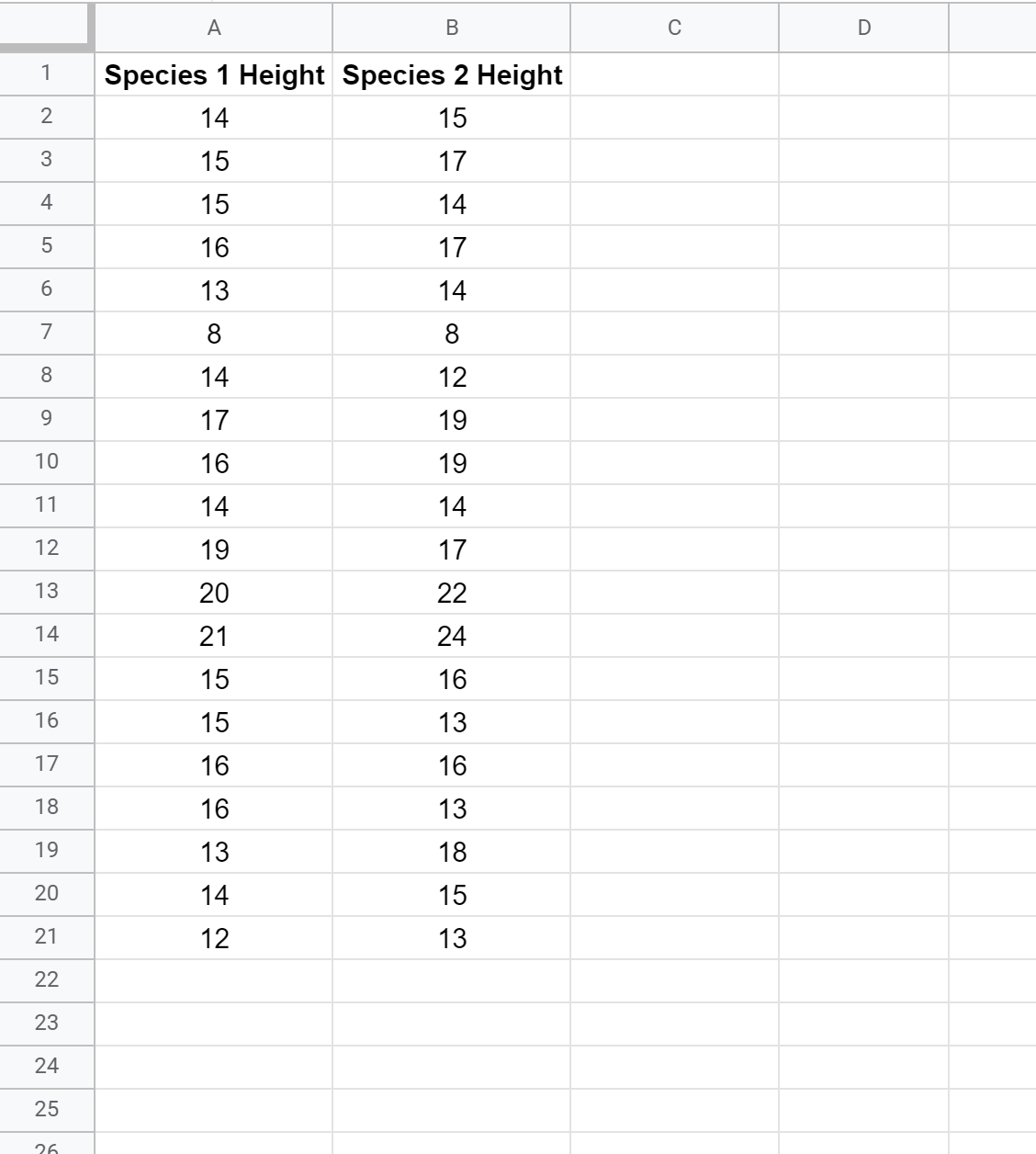
Stap 2: Bereken de t-test P-waarde

Laten we vervolgens zeggen dat we een t-test willen uitvoeren om te bepalen of de gemiddelde hoogte tussen de twee plantensoorten gelijk is.

De volgende schermafbeeldingen tonen de formules die moeten worden gebruikt om test-p-waarden te berekenen.

Gepaarde monsters t-test

We kunnen de volgende formule gebruiken om de p-waarde voor een t-test met gepaarde monsters te berekenen:

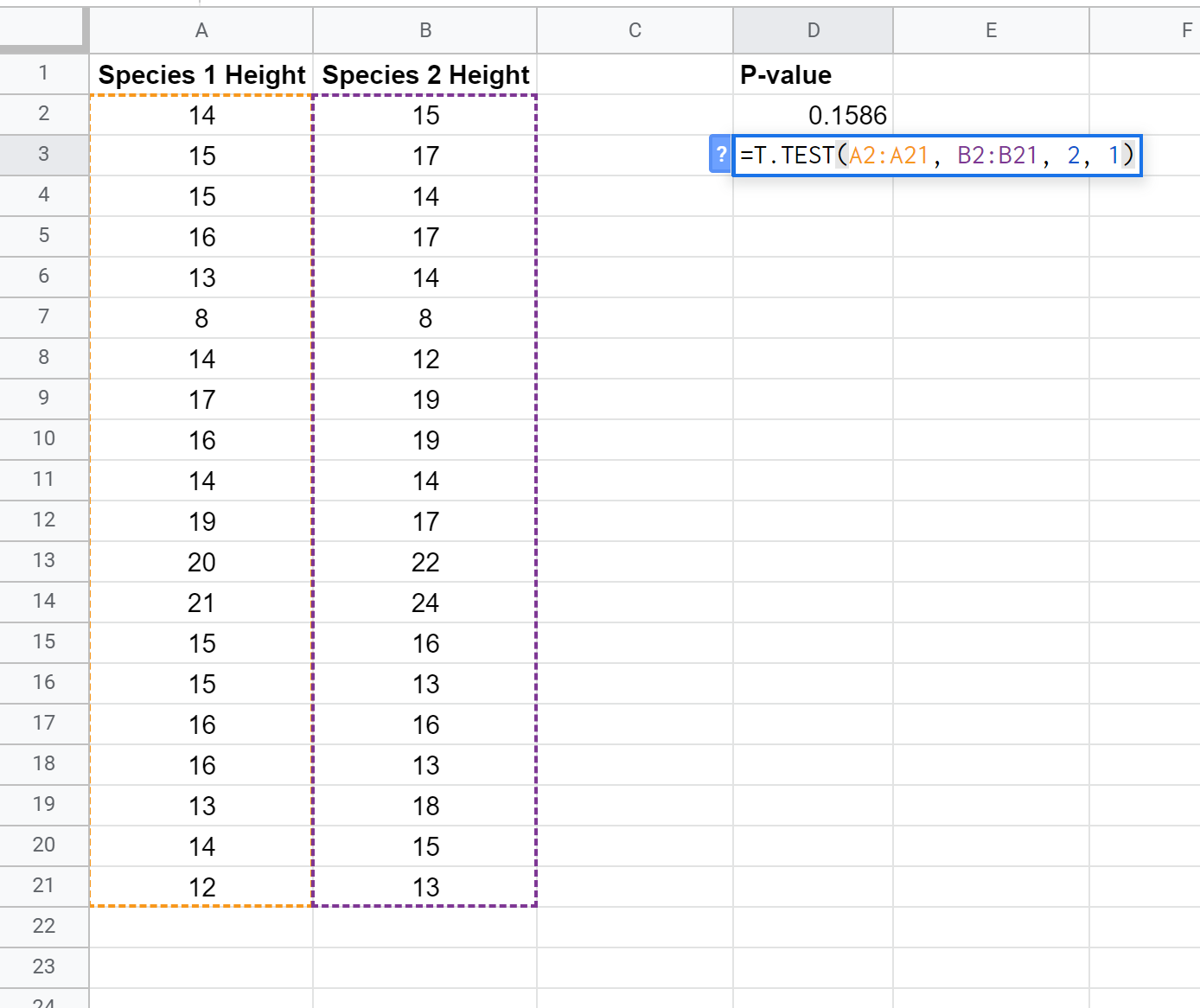
De p-waarde blijkt 0,1586 te zijn. Omdat dit niet minder is dan α = 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde hoogte tussen de twee soorten verschillend is.

T-test met twee steekproeven met gelijke variantie

We kunnen de volgende formule gebruiken om de p-waarde te berekenen voor een t-toets met twee steekproeven met gelijke variantie:

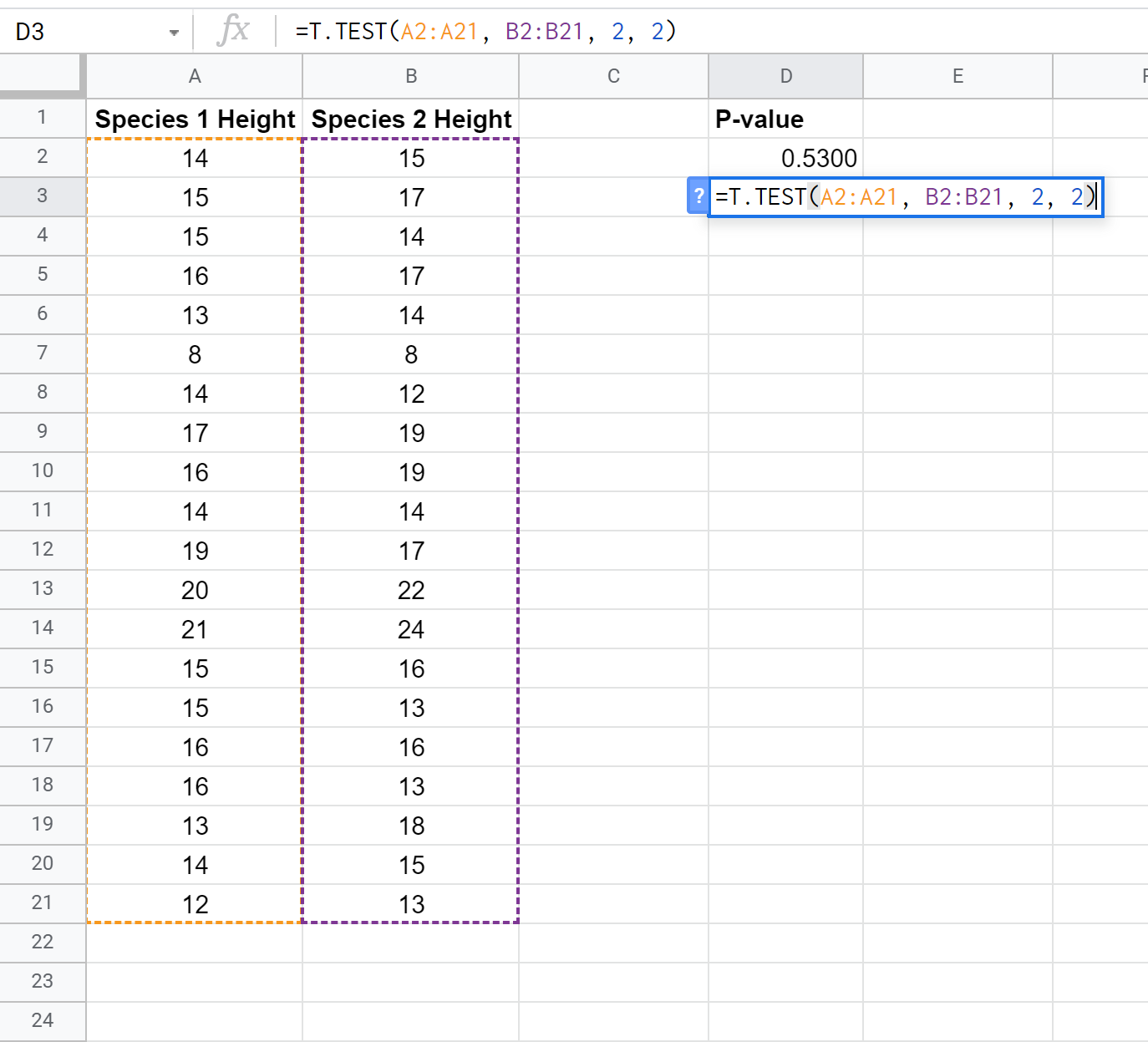
De p-waarde blijkt 0,5300 te zijn. Omdat dit niet minder is dan α = 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde hoogte tussen de twee soorten verschillend is.

T-test met twee steekproeven met ongelijke variantie

We kunnen de volgende formule gebruiken om de p-waarde te berekenen voor een t-toets met twee steekproeven met ongelijke variantie:

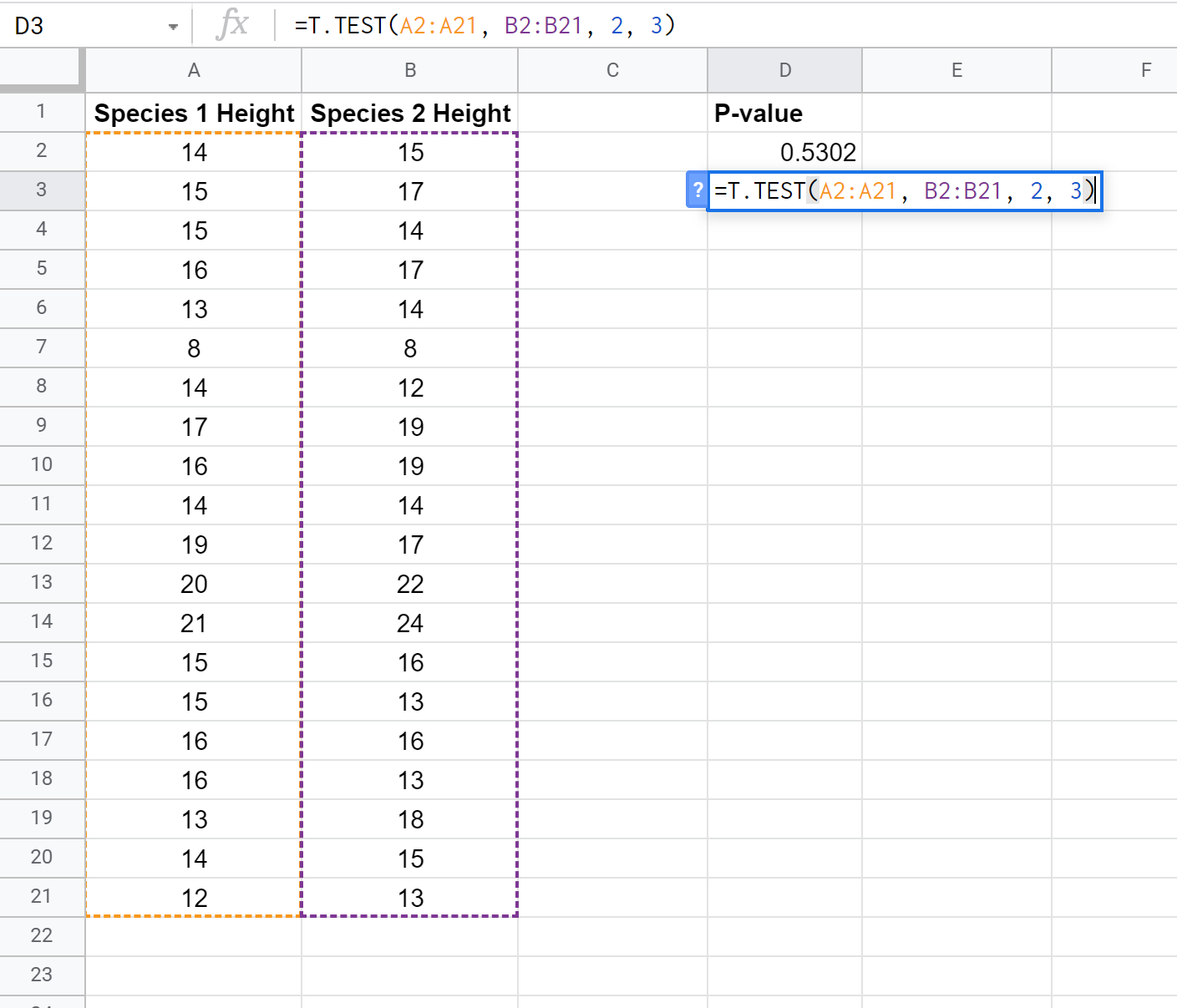
De p-waarde blijkt 0,5302 te zijn. Omdat dit niet minder is dan α = 0,05, slagen we er niet in de nulhypothese van de test te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde hoogte tussen de twee soorten verschillend is.

Aanvullende bronnen

Een uitleg van P-waarden en statistische significantie
Hoe u t-tests uitvoert in Google Spreadsheets
Eenrichtings-ANOVA uitvoeren in Google Spreadsheets