Hoe u een p-waarde kunt vinden uit een t-score in excel

In de statistiek zal een hypothesetest vaak resulteren in een T-score-teststatistiek. Zodra we die t-score hebben gevonden, vinden we meestal de bijbehorende p-waarde. Als deze p-waarde onder een bepaald alfaniveau ligt (bijvoorbeeld 0,10, 0,05, 0,01), dan verwerpen we de nulhypothese van de test en concluderen we dat onze resultaten significant zijn.

In deze zelfstudie wordt uitgelegd hoe u de p-waarde van een t-score in Excel kunt vinden met behulp van de functie T.DIST , waaraan de volgende argumenten moeten worden doorgegeven:

T.VERD (x, graden_vrijheid)

Goud:

• x: De T-score die ons interesseert.
• deg_freedom: De vrijheidsgraden.

Laten we een paar voorbeelden bekijken.

Voorbeeld 1: P-waarde uit t-score (tweezijdig)

Een botanicus wil weten of de gemiddelde hoogte van een bepaalde plantensoort gelijk is aan 45 centimeter. In een willekeurige steekproef van 12 planten ontdekt ze dat de gemiddelde hoogte van het monster 40,5 cm bedraagt en de standaardafwijking van het monster 1,37 cm.

Voer een tweezijdige hypothesetest uit met een alfaniveau van 0,05 om te bepalen of de gemiddelde lengte gelijk is aan 15 inch.

Stap 1: Formuleer de hypothesen.

De nulhypothese (H ₀ ): μ = 15

De alternatieve hypothese: (Ha): μ ≠ 15

Stap 2: Zoek de T-score en vrijheidsgraden.

score t = ( x -μ) / (s/√n) = (14,33-15) / (1,37/√12) = -1,694 .

vrijheidsgraden = n-1 = 12-1 = 11 .

Stap 3: Zoek de p-waarde van de t-score met behulp van Excel.

Om de p-waarde van de t-score te vinden, gebruiken we de volgende formule in Excel:

=T.VERD.2T(ABS(-1,694), 11)

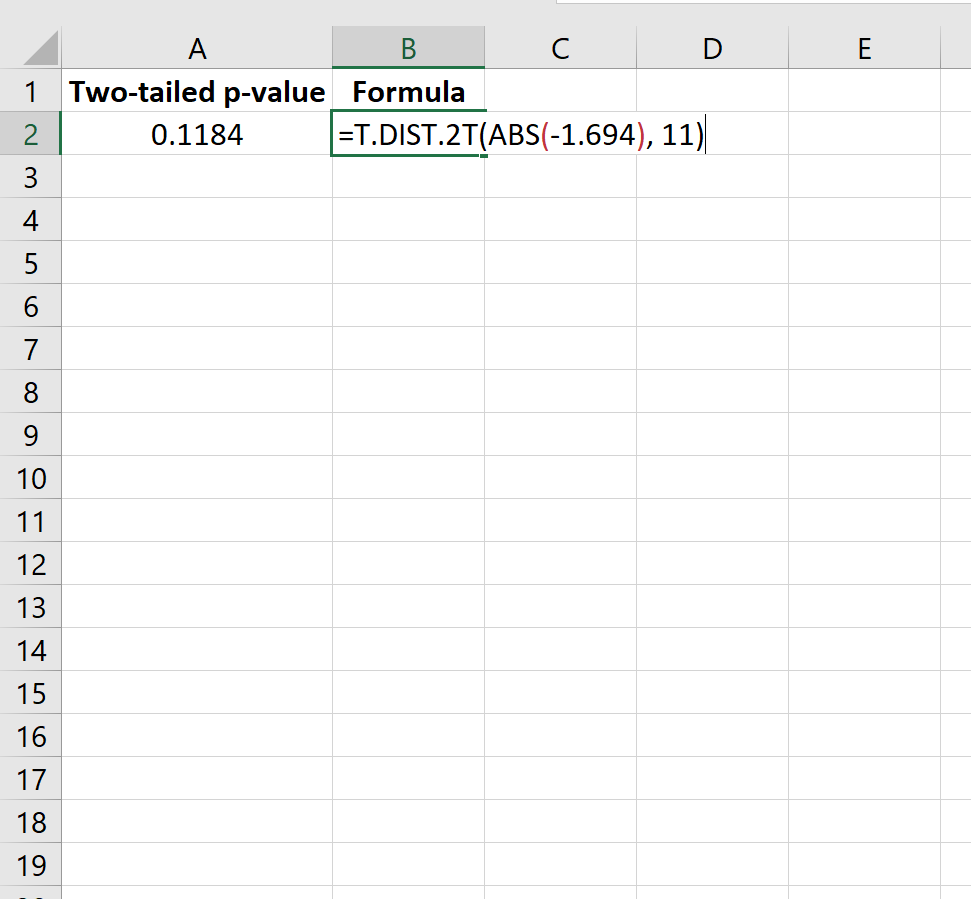
Dit vertelt ons dat de tweezijdige p-waarde 0,1184 is.

Stap 4: Verwerp de nulhypothese of verwerp deze niet.

Omdat de p-waarde van 0,1184 niet kleiner is dan het gekozen alfaniveau van 0,05 , slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat de gemiddelde planthoogte anders is dan 15 inch.

Voorbeeld 2: P-waarde uit T-score (eenzijdig)

Een bedrijf wil weten of een nieuw type batterij een langere gemiddelde levensduur heeft dan de huidige standaardbatterij, die een gemiddelde levensduur heeft van 18 uur. Uit een willekeurige steekproef van 25 nieuwe batterijen blijkt dat de gemiddelde levensduur 19 uur bedraagt met een standaarddeviatie van 4 uur.

Voer een eenzijdige hypothesetest uit met een alfaniveau van 0,05 om te bepalen of de gemiddelde levensduur van de nieuwe batterij langer is dan de gemiddelde levensduur van de huidige standaardbatterij.

Stap 1: Formuleer de hypothesen.

De nulhypothese (H ₀ ): μ ≤ 18

De alternatieve hypothese: (Ha): μ > 18

Stap 2: Zoek de T-score en vrijheidsgraden.

score t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .

vrijheidsgraden = n-1 = 25-1 = 24 .

Stap 3: Zoek de p-waarde van de t-score met behulp van Excel.

Om de p-waarde van de t-score te vinden, gebruiken we de volgende formule in Excel:

=T.VERD.RT(1,25, 24)

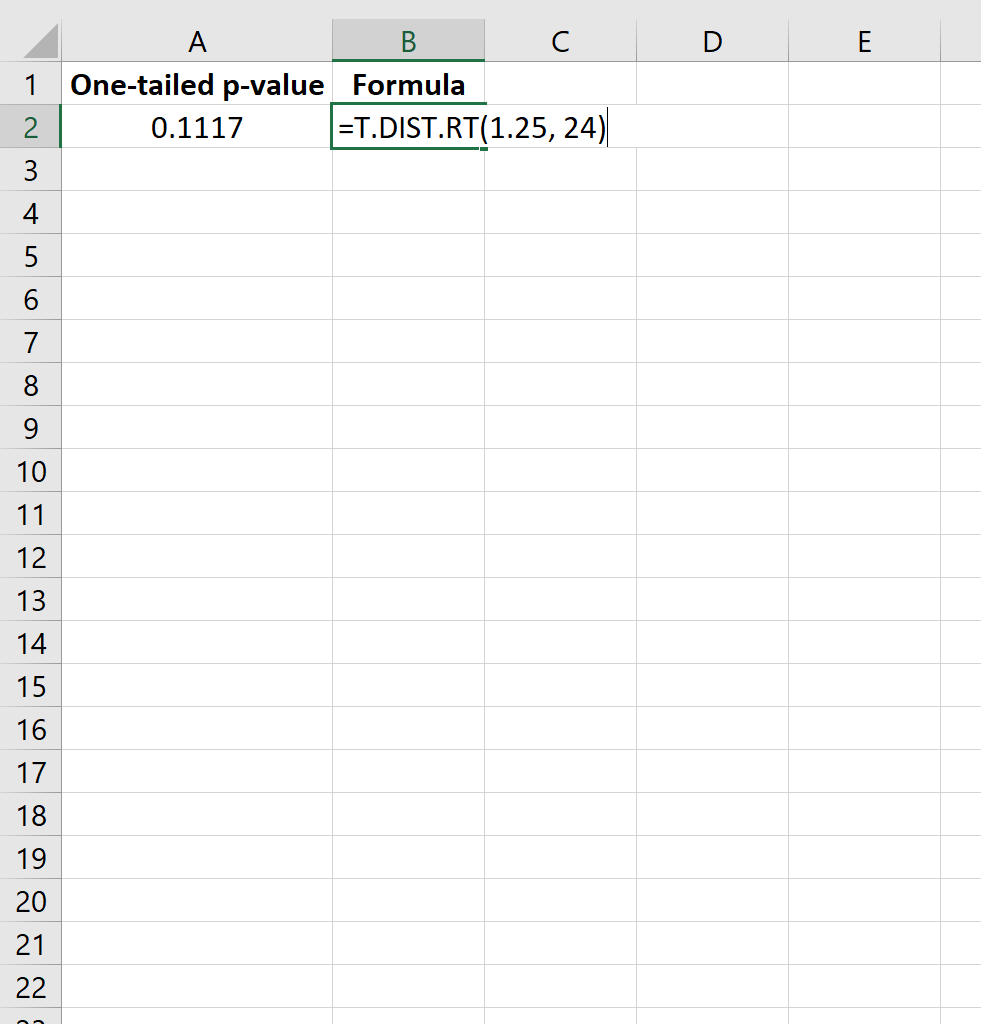
Dit vertelt ons dat de eenzijdige p-waarde 0,1117 is.

Stap 4: Verwerp de nulhypothese of verwerp deze niet.

Omdat de p-waarde van 0,1117 groter is dan het gekozen alfaniveau van 0,05 , slagen we er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat de gemiddelde levensduur van de nieuwe batterij langer is dan de gemiddelde levensduur van de huidige standaardbatterij.

Voor meer tutorials over statistieken in Excel kunt u onze volledige lijst met Excel-handleidingen raadplegen .