Pearson-correlatiecoëfficiënt

De Pearson-correlatiecoëfficiënt (ook bekend als de “product-moment correlatiecoëfficiënt”) is een maatstaf voor de lineaire associatie tussen twee variabelen X en Y. Deze heeft een waarde tussen -1 en 1 waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

De formule voor het vinden van de Pearson-correlatiecoëfficiënt

De formule voor het vinden van de Pearson-correlatiecoëfficiënt, aangeduid met r , voor een steekproef van gegevens is ( via Wikipedia ):

U zult deze formule waarschijnlijk nooit met de hand hoeven te berekenen, omdat u software kunt gebruiken om het voor u te doen, maar het is handig om te begrijpen wat deze formule precies doet door een voorbeeld te doorlopen.

Stel dat we de volgende dataset hebben:

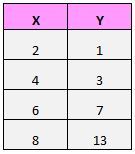
Als we deze paren (X, Y) in een spreidingsdiagram plotten, zou het er als volgt uitzien:

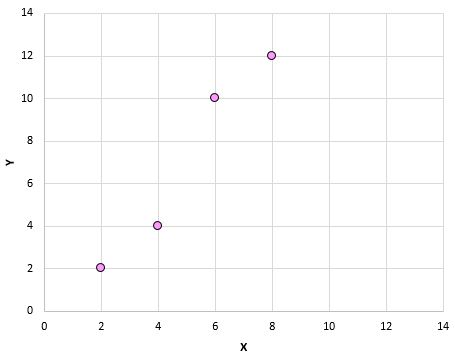
Alleen al door naar dit spreidingsdiagram te kijken, kunnen we zien dat er een positief verband bestaat tussen de variabelen X en Y: naarmate X toeneemt, heeft Y de neiging ook toe te nemen. Maar om precies te kwantificeren hoe positief deze twee variabelen met elkaar samenhangen, moeten we de Pearson-correlatiecoëfficiënt vinden.

Laten we ons concentreren op de teller van de formule:

Voor elk paar (X, Y) in onze dataset moeten we het verschil vinden tussen de x-waarde en de gemiddelde x-waarde, het verschil tussen de y-waarde en de gemiddelde y-waarde, en deze twee getallen vervolgens met elkaar vermenigvuldigen.

Ons eerste paar (X, Y) is bijvoorbeeld (2, 2). De gemiddelde waarde van x in deze dataset is 5 en de gemiddelde waarde van y in deze dataset is 7. Het verschil tussen de x-waarde van dit paar en de gemiddelde waarde van x is dus 2 – 5 = -3. Het verschil tussen de y-waarde van dit paar en de gemiddelde y-waarde is 2 – 7 = -5. Als we deze twee getallen vermenigvuldigen, krijgen we -3 * -5 = 15.

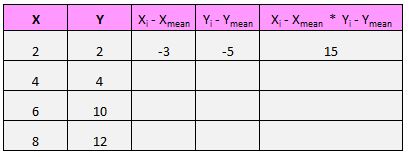
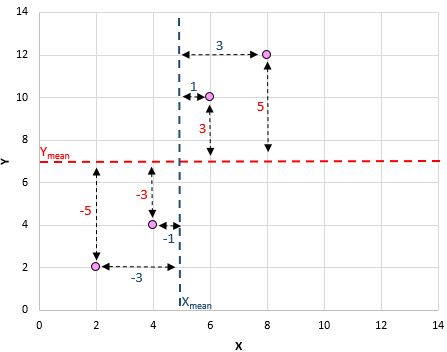
Hier is een visueel overzicht van wat we zojuist hebben gedaan:

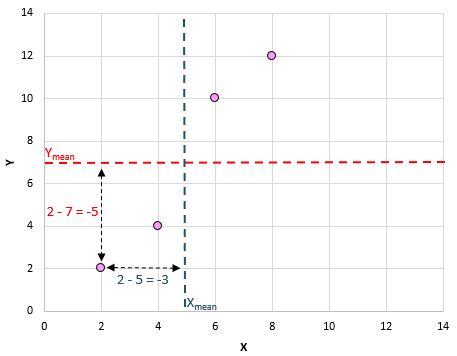
Doe dan dit voor elk paar:

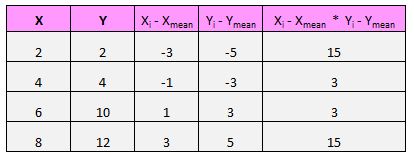
De laatste stap om de teller van de formule te krijgen, is door eenvoudigweg al deze waarden bij elkaar op te tellen:

15 + 3 +3 + 15 = 36

Vervolgens vertelt de noemer van de formule ons dat we de som van alle kwadratische verschillen voor x en y moeten vinden, deze twee getallen vervolgens met elkaar moeten vermenigvuldigen en vervolgens de vierkantswortel moeten nemen:

Dus eerst vinden we de som van de kwadraten van de verschillen voor x en y:

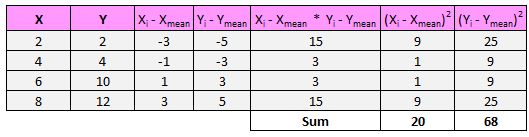
Vervolgens zullen we deze twee getallen met elkaar vermenigvuldigen: 20 * 68 = 1.360.

Ten slotte nemen we de vierkantswortel: √ 1.360 = 36,88

We ontdekten dus dat de teller van de formule 36 is en de noemer 36,88. Dit betekent dat onze Pearson-correlatiecoëfficiënt r = 36 / 36,88 = 0,976 is

Dit getal ligt dicht bij 1, wat aangeeft dat er een sterke positieve lineaire relatie bestaat tussen onze variabelen X en Y. Dit bevestigt de relatie die we in het spreidingsdiagram hebben waargenomen.

Bekijk correlaties

Bedenk dat een Pearson-correlatiecoëfficiënt ons het type lineaire relatie (positief, negatief, geen) tussen twee variabelen vertelt, evenals de sterkte van deze relatie (zwak, matig, sterk).

Wanneer we een spreidingsdiagram van twee variabelen maken, kunnen we de werkelijke relatie tussen twee variabelen zien . Hier volgen de vele soorten lineaire relaties die we kunnen waarnemen:

Sterk, positief verband: Naarmate de variabele op de x-as toeneemt, neemt de variabele op de y-as ook toe. De punten liggen dicht bij elkaar, wat wijst op een sterke relatie.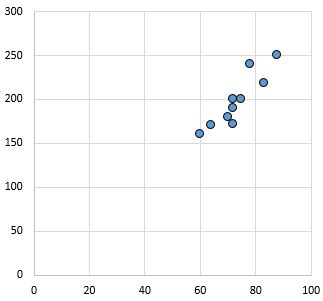

Pearson-correlatiecoëfficiënt: 0,94

Zwakke en positieve relatie: Naarmate de variabele op de x-as toeneemt, neemt de variabele op de y-as ook toe. De punten liggen nogal verspreid, wat wijst op een zwakke relatie.

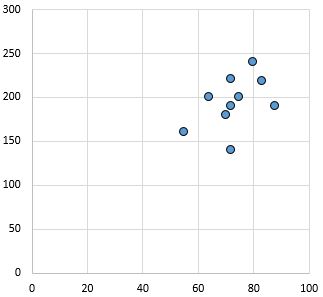
Pearson-correlatiecoëfficiënt: 0,44

Geen relatie: Er is geen duidelijke relatie (positief of negatief) tussen de variabelen.

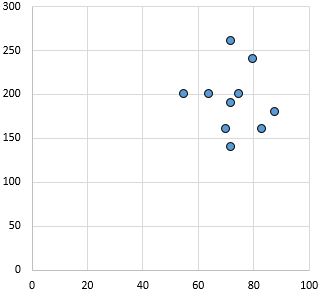
Pearson-correlatiecoëfficiënt: 0,03

Sterk, negatief verband: Naarmate de variabele op de x-as toeneemt, neemt de variabele op de y-as af. De punten liggen dicht op elkaar, wat wijst op een sterke relatie.

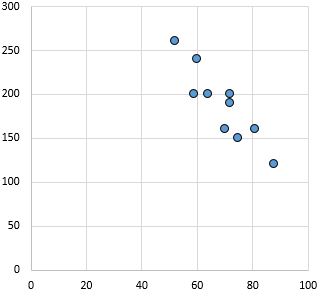
Pearson-correlatiecoëfficiënt: -0,87

Zwakke en negatieve relatie: Naarmate de variabele op de x-as toeneemt, neemt de variabele op de y-as af. De punten liggen nogal verspreid, wat wijst op een zwakke relatie.

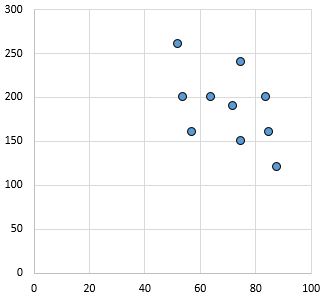
Pearson-correlatiecoëfficiënt: – 0,46

Het testen van de significantie van een Pearson-correlatiecoëfficiënt

Wanneer we de Pearson-correlatiecoëfficiënt voor een reeks gegevens vinden, werken we vaak met een steekproef van gegevens uit een grotere populatie . Dit betekent dat het mogelijk is om een correlatie anders dan nul te vinden voor twee variabelen, zelfs als deze feitelijk niet gecorreleerd zijn in de totale populatie.

Stel dat we bijvoorbeeld voor elk gegevenspunt in de gehele populatie een spreidingsdiagram maken voor de variabelen X en Y , en dat ziet er als volgt uit:

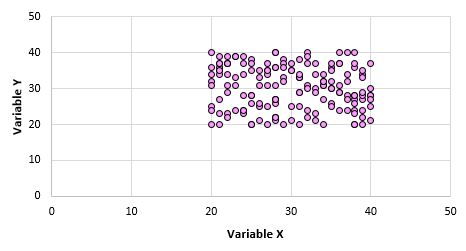
Het is duidelijk dat deze twee variabelen niet met elkaar gecorreleerd zijn. Het is echter mogelijk dat wanneer we een steekproef van 10 punten uit de populatie nemen, we de volgende punten kiezen:

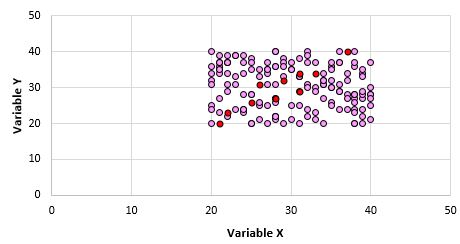
We kunnen zien dat de Pearson-correlatiecoëfficiënt voor deze steekproef van punten 0,93 bedraagt, wat wijst op een sterke positieve correlatie, ook al is de populatiecorrelatie nul.

Om te testen of een correlatie tussen twee variabelen statistisch significant is of niet, kunnen we de volgende teststatistiek vinden:

Teststatistiek T = r * √ (n-2) / (1-r ² )

waarbij n het aantal paren in onze steekproef is, r de Pearson-correlatiecoëfficiënt is en de T-teststatistiek een verdeling volgt met n-2 vrijheidsgraden.

Laten we een voorbeeld bekijken van hoe u de significantie van een Pearson-correlatiecoëfficiënt kunt testen.

Voorbeeld

De volgende dataset toont de lengte en het gewicht van 12 personen:

Het onderstaande spreidingsdiagram toont de waarde van deze twee variabelen:

De Pearson-correlatiecoëfficiënt voor deze twee variabelen is r = 0,836.

De teststatistiek T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Volgens onze t-verdelingscalculator heeft een score van 4,804 met 10 vrijheidsgraden een p-waarde van 0,0007. Omdat 0,0007 < 0,05 kunnen we concluderen dat de correlatie tussen gewicht en lengte in dit voorbeeld statistisch significant is bij alfa = 0,05.

Voorzorgsmaatregelen

Hoewel een Pearson-correlatiecoëfficiënt nuttig kan zijn om ons te vertellen of twee variabelen al dan niet een lineair verband hebben, moeten we drie dingen in gedachten houden bij het interpreteren van een Pearson-correlatiecoëfficiënt:

1. Correlatie impliceert geen oorzakelijk verband. Het is niet omdat twee variabelen gecorreleerd zijn dat de ene er noodzakelijkerwijs voor zorgt dat de andere vaker of minder vaak voorkomt. Een klassiek voorbeeld hiervan is de positieve correlatie tussen de verkoop van ijs en aanvallen van haaien. Wanneer de verkoop van ijs in bepaalde periodes van het jaar toeneemt, nemen de aanvallen van haaien ook toe.

Betekent dit dat het eten van ijs haaienaanvallen veroorzaakt ? Natuurlijk niet! Dit betekent eenvoudigweg dat in de zomer het ijsverbruik en de aanvallen van haaien toenemen, omdat ijs in de zomer populairder is en er in de zomer meer mensen de oceaan in gaan.

2. Correlaties zijn gevoelig voor uitschieters. Een extreme uitbijter kan een Pearson-correlatiecoëfficiënt aanzienlijk veranderen. Beschouw het onderstaande voorbeeld:

De variabelen X en Y hebben een Pearson-correlatiecoëfficiënt van 0,00 . Maar stel je voor dat we een uitbijter in de dataset hebben:

De Pearson-correlatiecoëfficiënt voor deze twee variabelen is echter 0,878 . Deze ene uitbijter verandert alles. Dit is de reden waarom het bij het berekenen van de correlatie voor twee variabelen een goed idee is om de variabelen te visualiseren met behulp van een spreidingsdiagram om te controleren op uitschieters.

3. Een Pearson-correlatiecoëfficiënt geeft geen niet-lineaire relaties tussen twee variabelen weer. Laten we ons voorstellen dat we twee variabelen hebben met de volgende relatie:

De Pearson-correlatiecoëfficiënt voor deze twee variabelen is 0,00 omdat ze geen lineair verband hebben. Deze twee variabelen hebben echter een niet-lineair verband: de y-waarden zijn simpelweg de x-waarden in het kwadraat.

Houd er bij het gebruik van de Pearson-correlatiecoëfficiënt rekening mee dat u eenvoudigweg test of twee variabelen lineair gerelateerd zijn. Zelfs als een Pearson-correlatiecoëfficiënt ons vertelt dat twee variabelen niet gecorreleerd zijn, kunnen ze nog steeds een soort niet-lineaire relatie hebben. Dit is nog een reden waarom het nuttig is om een spreidingsdiagram te maken bij het analyseren van de relatie tussen twee variabelen: het kan je helpen een niet-lineaire relatie te detecteren.