Pearson-correlatiecoëfficiënt
In dit artikel wordt uitgelegd wat de Pearson-correlatiecoëfficiënt (of lineaire correlatiecoëfficiënt) is en waarvoor deze wordt gebruikt. Aan de hand van een stapsgewijze oefening ontdekt u hoe u de Pearson-correlatiecoëfficiënt kunt berekenen. Bovendien kunt u aan het einde de Pearson Correlatiecoëfficiëntwaarde van elke dataset vinden met de online rekenmachine.
Wat is de correlatiecoëfficiënt van Pearson?
De Pearson-correlatiecoëfficiënt , ook wel de lineaire correlatiecoëfficiënt of eenvoudigweg de correlatiecoëfficiënt genoemd, is een statistische maatstaf die de relatie tussen twee variabelen aangeeft.
Om de Pearson-correlatiecoëfficiënt tussen twee variabelen te berekenen, moet u de covariantie van genoemde variabelen delen door de vierkantswortel van het product van hun varianties.
De Pearson-correlatiecoëfficiënt probeert dus de lineaire afhankelijkheid tussen twee kwantitatieve willekeurige variabelen te kwantificeren. A priori is het numeriek evalueren van de correlatie tussen variabelen ingewikkeld omdat het moeilijk is om te bepalen dat het paar variabelen meer gecorreleerd is als, zoals in pues, het doel van Pearson’s correlatiecoëfficiënt is om de relatie tussen variabelen te waarderen om zo de relatie tussen variabelen te kunnen waarderen. vergelijk ze onderling.
De waarde van de Pearson-correlatie-index ligt tussen -1 en +1. We zullen hieronder zien hoe de waarde van de Pearson-correlatiecoëfficiënt wordt geïnterpreteerd.
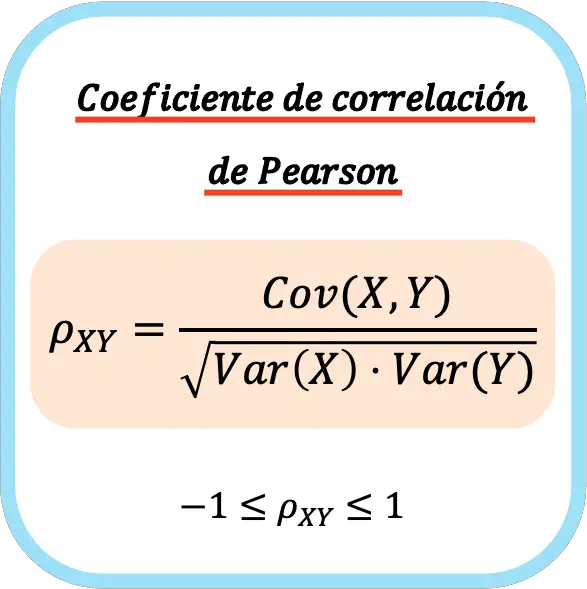
Pearson-correlatiecoëfficiëntformule
De Pearson-correlatiecoëfficiënt van twee statistische variabelen is gelijk aan het quotiënt tussen de covariantie van de variabelen en de vierkantswortel van het product van de variantie van elke variabele.
Daarom is de formule voor het berekenen van de Pearson-correlatiecoëfficiënt als volgt:
👉 U kunt de onderstaande rekenmachine gebruiken om de Pearson-correlatiecoëfficiënt voor elke dataset te berekenen.
Wanneer de Pearson-correlatiecoëfficiënt voor een populatie wordt berekend, wordt deze doorgaans uitgedrukt met de Griekse letter ρ. Maar wanneer de coëfficiënt wordt berekend ten opzichte van een monster, wordt meestal de letter r als symbool gebruikt.
Houd er rekening mee dat het voor het bepalen van de Pearson-correlatiecoëfficiënt essentieel is dat u weet hoe u de covariantie tussen twee variabelen en de variantie van een variabele berekent. Bovendien moet u begrijpen wat deze statistische metingen betekenen. Voordat u verdergaat met de uitleg, is het daarom raadzaam de volgende twee artikelen te lezen:
Voorbeeld van het berekenen van de Pearson-correlatiecoëfficiënt
Gezien de definitie van de Pearson-correlatiecoëfficiënt en de bijbehorende formule, vindt u hieronder een stapsgewijs voorbeeld, zodat u kunt zien hoe deze wordt berekend.
- Bereken de Pearson-correlatiecoëfficiënt tussen de volgende twee continue variabelen:

Voordat we de Pearson-correlatiecoëfficiënt berekenen, zullen we de dataset in een spreidingsdiagram weergeven om de relatie tussen de twee variabelen te analyseren:
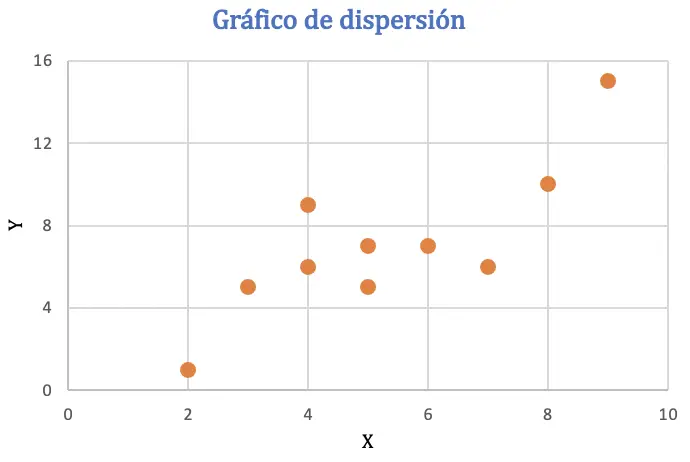
Uit het spreidingsdiagram kan worden afgeleid dat de gegevens een positieve trend kunnen vertonen, of met andere woorden: wanneer de ene variabele in waarde stijgt, neemt de andere variabele ook toe. Om de correlatie te controleren, zullen we de Pearson-coëfficiënt vinden.
Het eerste dat u moet doen, is het rekenkundig gemiddelde van elke variabele afzonderlijk vinden, wat overeenkomt met de totale som van de gegevens gedeeld door het aantal waarnemingen.
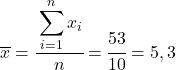
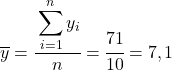
Nu we het gemiddelde van elke variabele kennen, moeten we de volgende kolommen aan de gegevenstabel toevoegen:
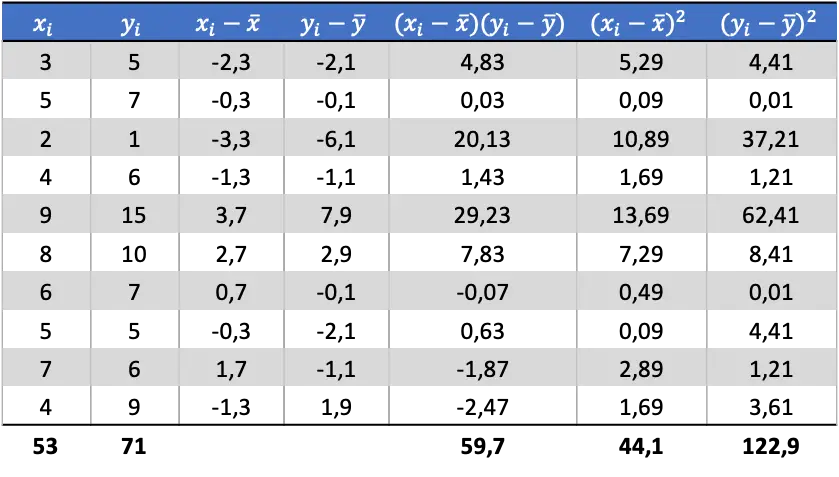
Uit de berekende gegevens in de tabel bepalen we de waarden van de covariantie en varianties (als je niet meer weet hoe dit is gedaan, staan er hierboven twee links waar dit in detail wordt uitgelegd):
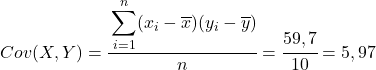
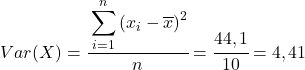
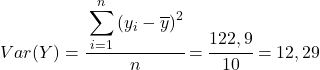
Pas ten slotte eenvoudigweg de Pearson-correlatiecoëfficiëntformule toe om de waarde ervan te verkrijgen:
![]()
De Pearson-correlatiecoëfficiënt heeft een waarde die zeer dicht bij 1 ligt, wat betekent dat deze twee variabelen een vrij sterke positieve correlatie hebben.
Zoals je hebt gezien, is het voor het bepalen van de Pearson-correlatiecoëfficiënt erg handig om programma’s als Excel te gebruiken om kolomberekeningen sneller uit te voeren.
Pearson-correlatiecoëfficiëntcalculator
Voer een reeks statistische gegevens in de volgende rekenmachine in om de Pearson-correlatiecoëfficiënt tussen twee variabelen te berekenen. U moet de gegevensparen scheiden, zodat in het eerste vak alleen de waarden van één variabele staan en in het tweede vak alleen de waarden van de tweede variabele.
Gegevens moeten worden gescheiden door een spatie en moeten worden ingevoerd met de punt als decimaal scheidingsteken.
Interpretatie van de Pearson-correlatiecoëfficiënt
In deze sectie zullen we zien hoe we de Pearson-correlatiecoëfficiënt moeten interpreteren, omdat het niet voldoende is om de waarde ervan te kennen, maar je moet wel weten hoe je de betekenis ervan moet analyseren.
De interpretatie van de Pearson-correlatiecoëfficiënt hangt dus af van de waarde ervan:
- r=-1 : de twee variabelen hebben een perfecte negatieve correlatie, dus we kunnen een lijn tekenen met een negatieve helling waarin alle punten met elkaar verbonden zijn.
- -1<r<0 : de correlatie tussen de twee variabelen is negatief, dus als de ene variabele toeneemt, neemt de andere af. Hoe dichter de waarde bij -1 ligt, hoe negatiever de variabelen gerelateerd zijn.
- r=0 : de correlatie tussen de twee variabelen is erg zwak; de lineaire relatie daartussen is zelfs nul. Dit betekent niet dat de variabelen onafhankelijk zijn, aangezien ze een niet-lineair verband kunnen hebben.
- 0<r<1 : de correlatie tussen de twee variabelen is positief, hoe dichter de waarde bij +1 ligt, hoe sterker de relatie tussen de variabelen. In dit geval heeft de ene variabele de neiging in waarde te stijgen wanneer de andere ook toeneemt.
- r=1 : de twee variabelen hebben een perfecte positieve correlatie, dat wil zeggen, ze hebben een positieve lineaire relatie.
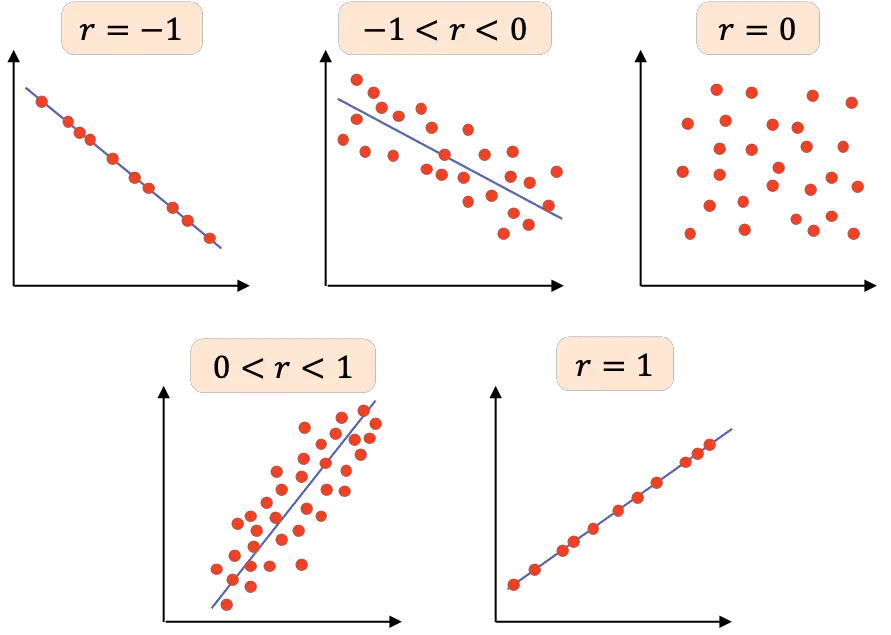
Samenvattend wordt de volgende tabel weergegeven met de verschillende interpretaties van de Pearson-correlatiecoëfficiënt:
| Waarde | Interpretatie |
|---|---|
| r=-1 | Perfecte negatieve correlatie. |
| -1<r<0 | Negatieve correlatie: hoe dichter de correlatie bij -1 ligt, hoe sterker deze is. |
| r=0 | Nul lineaire correlatie. |
| 0<r<1 | Positieve correlatie: hoe dichter de correlatie bij +1 ligt, hoe sterker deze is. |
| r=1 | Perfecte positieve correlatie. |
Houd er rekening mee dat zelfs als er een verband bestaat tussen twee variabelen, dit niet betekent dat er causaliteit tussen beide variabelen bestaat, dat wil zeggen dat de correlatie tussen twee variabelen niet betekent dat de verandering in een variabele de oorzaak is van de verandering van de variabele. andere variabele.
Als we bijvoorbeeld ontdekken dat er een positieve relatie bestaat tussen de productie van twee verschillende hormonen in het lichaam, is het niet nodig dat een toename van het ene hormoon leidt tot een toename van het andere hormoon. Het kan zijn dat het lichaam beide hormonen produceert omdat het beide nodig heeft om een ziekte te bestrijden en daarom de niveaus van beide tegelijkertijd verhoogt, in welk geval de oorzaak de ziekte zou zijn. Om te bepalen of er een causaal verband bestaat tussen de twee hormonen, moet verder onderzoek worden uitgevoerd.