De vijf hypothesen van pearson's correlatie

De Pearson-correlatiecoëfficiënt (ook bekend als de “product-moment correlatiecoëfficiënt”) meet de lineaire associatie tussen twee variabelen.

Er is altijd een waarde tussen -1 en 1 nodig, waarbij:

• -1 geeft een perfect negatieve lineaire correlatie aan tussen twee variabelen
• 0 geeft aan dat er geen lineaire correlatie is tussen twee variabelen
• 1 geeft een perfect positieve lineaire correlatie aan tussen twee variabelen

Voordat we echter de Pearson-correlatiecoëfficiënt tussen twee variabelen berekenen, moeten we ervoor zorgen dat aan vijf aannames wordt voldaan:

1. Meetniveau: Beide variabelen moeten worden gemeten op interval- of rationiveau .

2. Lineair verband: Er moet een lineair verband bestaan tussen de twee variabelen.

3. Normaliteit: beide variabelen moeten ongeveer normaal verdeeld zijn.

4. Gerelateerde paren: Elke waarneming in de dataset moet een paar waarden hebben.

5. Geen uitschieters: Er mogen geen extreme uitschieters in de dataset voorkomen.

In dit artikel geven we een uitleg van elke aanname en hoe je kunt bepalen of aan de aanname is voldaan.

Hypothese 1: Meetniveau

Om een Pearson-correlatiecoëfficiënt tussen twee variabelen te berekenen, moeten beide variabelen op interval- of rationiveau worden gemeten.

De volgende afbeelding geeft een korte uitleg van de vier niveaus waarop variabelen kunnen worden gemeten:

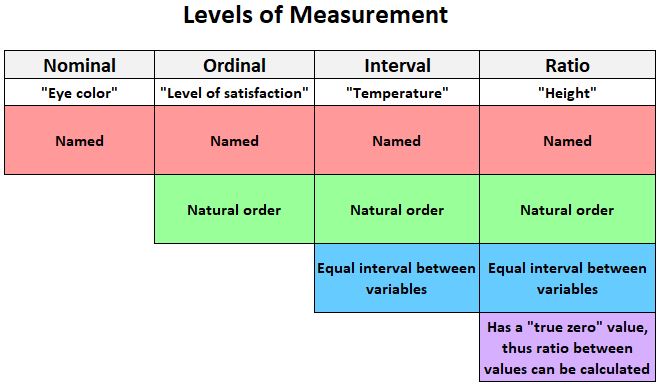
Hier volgen enkele voorbeelden van variabelen die op een intervalschaal kunnen worden gemeten:

• Temperatuur: Gemeten in Fahrenheit of Celsius
• Kredietscores: gemeten van 300 tot 850
• SAT-scores: gemeten van 400 tot 1.600

Hier volgen enkele voorbeelden van variabelen die op een ratioschaal kunnen worden gemeten:

• Hoogte: Gemeten in centimeters, inches, voeten, enz.
• Gewicht: gemeten in kilogram, pond, enz.
• Lengte: Gemeten in centimeters, inches, voeten, enz.

Als de variabelen op ordinaal niveau worden gemeten, moet u de Spearman-correlatiecoëfficiënt daartussen berekenen.

Gerelateerd: Meetniveaus: Nominaal, Ordinaal, Interval en Ratio

Hypothese 2: Lineair verband

Om een Pearson-correlatiecoëfficiënt tussen twee variabelen te berekenen, moet er een lineair verband bestaan tussen de twee variabelen.

De eenvoudigste manier om deze hypothese te testen is door eenvoudigweg een spreidingsdiagram van de twee variabelen te maken. Als de punten op de grafiek ongeveer een rechte lijn volgen, is er sprake van een lineair verband:

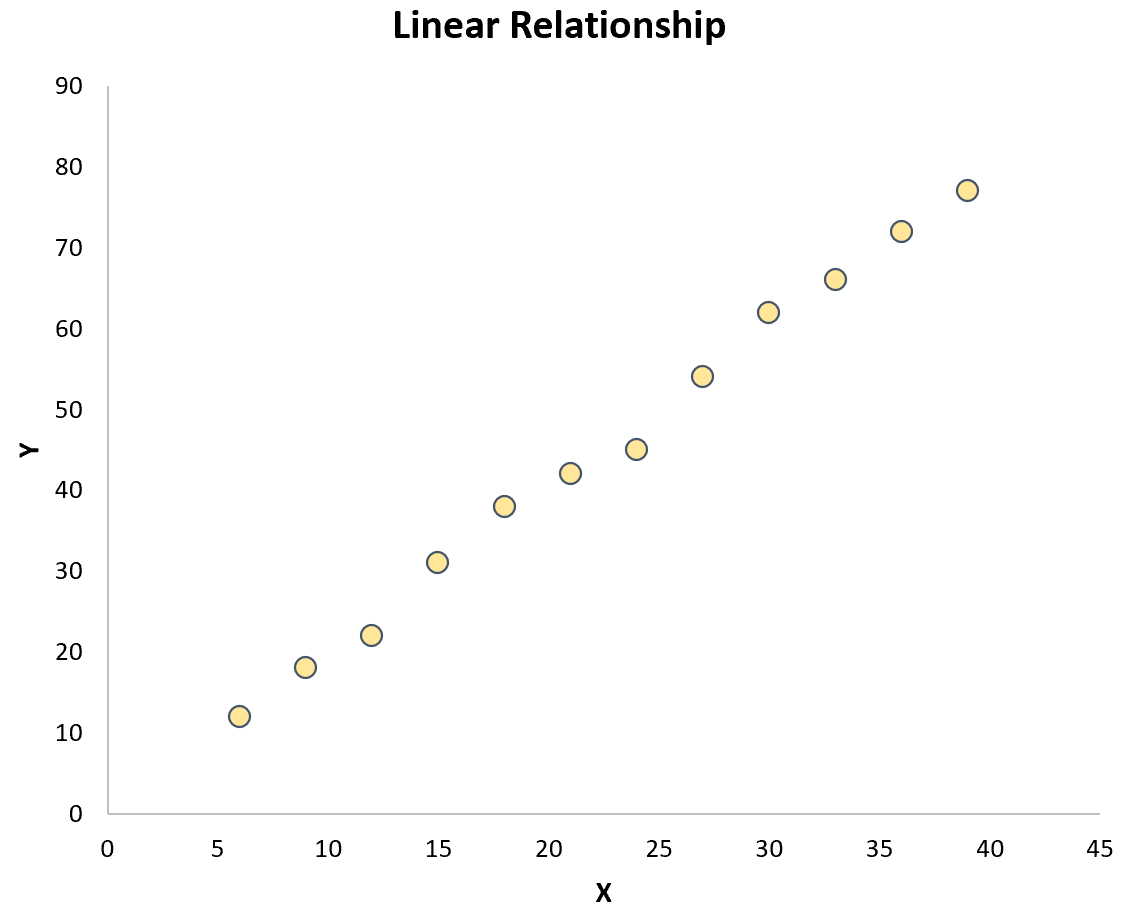
Als de punten echter willekeurig over de plot verspreid zijn of een ander soort relatie hebben (zoals kwadratisch), bestaat er geen lineaire relatie tussen de variabelen:

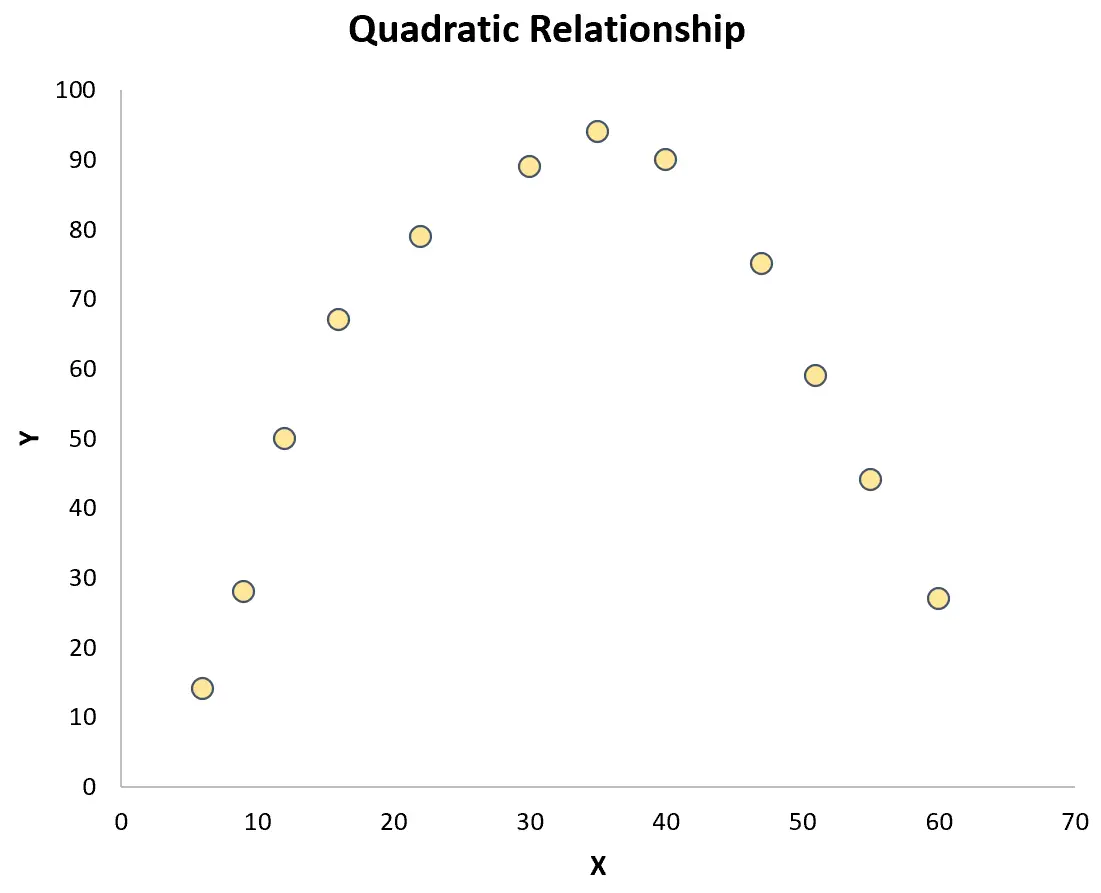
In dit geval zal een Pearson-correlatiecoëfficiënt de relatie tussen de variabelen niet adequaat weergeven.

Hypothese 3: normaliteit

Een Pearson-correlatiecoëfficiënt veronderstelt ook dat de twee variabelen bij benadering normaal verdeeld zijn.

U kunt deze aanname visueel verifiëren door voor elke variabele een histogram of QQ-plot te maken.

1. Histogram

Als het histogram van een gegevensset grofweg klokvormig is, is het waarschijnlijk dat de gegevens normaal verdeeld zijn.

2. QQLand

Een QQ-plot, een afkorting van ‚quantile-quantile‘, is een type plot dat theoretische kwantielen langs de x-as weergeeft (dat wil zeggen waar uw gegevens zich zouden bevinden als deze een normale verdeling zouden volgen) en kwantielen van monsters langs de y-as. (dwz waar uw gegevens zich daadwerkelijk bevinden).

Als de gegevenswaarden een min of meer rechte lijn volgen die een hoek van 45 graden vormt, wordt aangenomen dat de gegevens normaal verdeeld zijn.

U kunt ook een formele statistische test uitvoeren om te bepalen of een variabele normaal verdeeld is.

Als de p-waarde van de test onder een bepaald significantieniveau ligt (zoals α = 0,05), dan heb je voldoende bewijs om te zeggen dat de gegevens niet normaal verdeeld zijn.

Er zijn drie statistische tests die vaak worden gebruikt om de normaliteit te testen:

1. De Jarque-Bera-test

• Hoe u een Jarque-Bera-test uitvoert in Excel
• Een Jarque-Bera-test uitvoeren in R
• Hoe u een Jarque-Bera-test uitvoert in Python

2. De Shapiro-Wilk-test

• Hoe een Shapiro-Wilk-test uit te voeren in R
• Hoe u een Shapiro-Wilk-test uitvoert in Python

3. De Kolmogorov-Smirnov-test

• Hoe een Kolmogorov-Smirnov-test uit te voeren in R
• Hoe u een Kolmogorov-Smirnov-test uitvoert in Python

Hypothese 4: Gerelateerde paren

Een Pearson-correlatiecoëfficiënt gaat er ook van uit dat elke waarneming in de dataset een paar waarden moet hebben.

Deze hypothese is eenvoudig te verifiëren. Als u bijvoorbeeld de correlatie tussen gewicht en lengte berekent, controleert u eenvoudigweg of elke waarneming in de gegevensset een maatstaf voor gewicht en een maatstaf voor lengte heeft.

Hypothese 5: Geen uitschieters

Een Pearson-correlatiecoëfficiënt gaat er ook van uit dat er geen extreme uitschieters in de dataset voorkomen, omdat uitschieters de berekening van de correlatiecoëfficiënt sterk beïnvloeden.

Om dit te illustreren, bekijken we de volgende dataset:

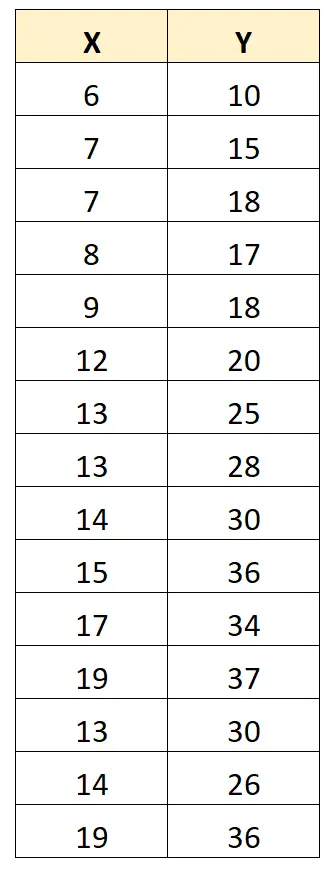
De Pearson-correlatiecoëfficiënt tussen X en Y is 0,949 .

Stel echter dat we een uitbijter in de dataset hebben:

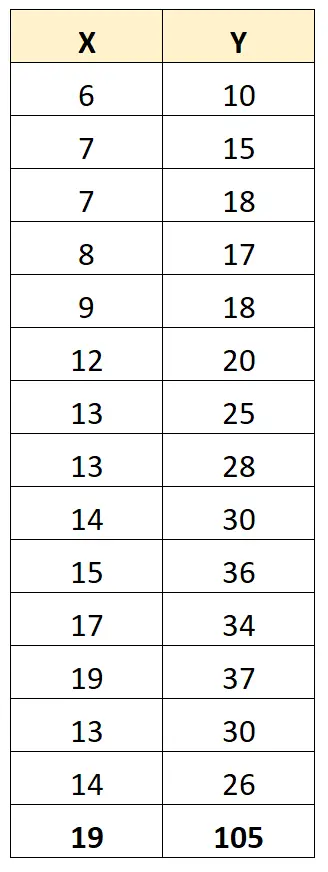
De Pearson-correlatiecoëfficiënt tussen X en Y is nu 0,711 .

Een uitschieter verandert de Pearson-correlatiecoëfficiënt tussen de twee variabelen aanzienlijk. In dit geval kan het zinvol zijn om de uitschieter uit de dataset te verwijderen.

Gerelateerd: De complete gids: Wanneer u uitschieters in gegevens moet verwijderen

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over de Pearson-correlatie:

Inleiding tot de Pearson-correlatiecoëfficiënt
Hoe Pearson-correlatie in APA-formaat te rapporteren
Hoe u handmatig een Pearson-correlatiecoëfficiënt kunt berekenen