Percentiel, kwartiel en kwantiel: wat is het verschil?

Drie termen die studenten vaak verwarren in de statistiek zijn percentielen, kwartielen en kwantielen.

Hier is een eenvoudige definitie van elk:

Percentielen: bereik van 0 tot 100.

Kwartielen: bereik van 0 tot 4.

Kwantielen: ga van een willekeurige waarde naar een andere waarde.

Merk op dat percentielen en kwartielen eenvoudigweg soorten kwantielen zijn.

Sommige soorten kwantielen hebben zelfs specifieke namen, waaronder:

• De 4 kwantielen worden kwartielen genoemd.
• De 5 kwantielen worden kwintielen genoemd.
• De 8 kwantielen worden oktielen genoemd.
• De 10 kwantielen worden decielen genoemd.
• De 100 kwantielen worden percentielen genoemd.

Merk op dat percentielen en kwartielen de volgende relatie delen:

• 0 percentiel = 0 kwartiel (ook wel minimum genoemd)
• 25e percentiel = 1e kwartiel
• 50e percentiel = 2e kwartiel (ook wel mediaan genoemd)
• 75e percentiel = 3e kwartiel
• 100e percentiel = 4e kwartiel (ook wel maximum genoemd)

Voorbeeld: percentielen en kwartielen vinden

Stel dat we de volgende dataset hebben met 20 waarden:

Met behulp van statistische software (zoals Excel, R, Python, enz.) kunnen we de volgende percentielen en kwartielen voor deze dataset vinden:

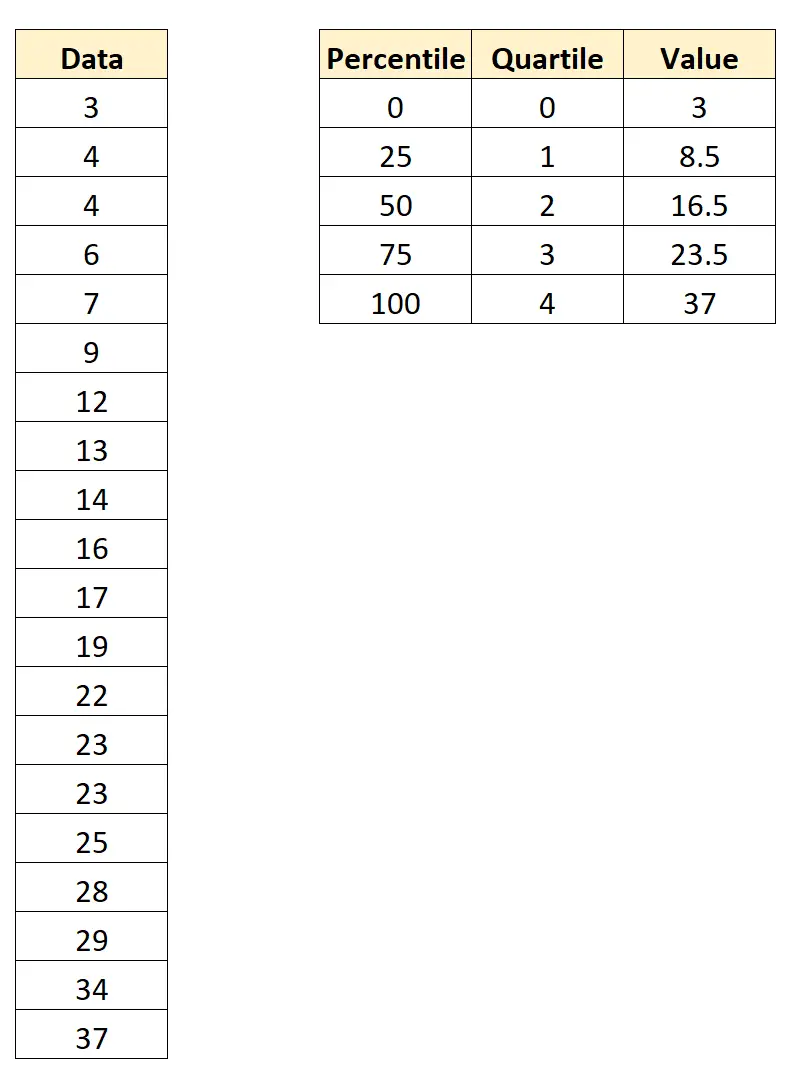
Zo interpreteert u deze waarden:

• Percentiel 0 en kwartiel 0 zijn 3 .
• Het 25e percentiel en het 1e kwartiel is 8,5 .
• Het 50e percentiel en het 2e kwartiel is 16,5 .
• Het 75e percentiel en het 3e kwartiel is 23,5 .
• Het 100e percentiel en het 4e kwartiel zijn 37 .

Wanneer percentielen versus kwartielen gebruiken?

Percentielen kunnen worden gebruikt om vragen te beantwoorden zoals:

Hoeveel moet een leerling op een bepaalde toets scoren om tot de top 10% te behoren?

Om deze vraag te beantwoorden, zouden we het 90e percentiel van alle scores vinden, wat de waarde is die de onderste 90% scheidt van de bovenste 10%.

Welke hoogten omvatten de 40% van de gemiddelde lengte van leerlingen op een bepaalde school?

Om deze vraag te beantwoorden, zouden we het 70e percentiel van hoogten en het 30e percentiel van hoogten vinden, de twee waarden die de boven- en ondergrenzen voor de middelste 40% van de hoogten bepalen.

Kwartielen kunnen worden gebruikt om vragen te beantwoorden zoals:

Hoeveel moet een leerling op een toets scoren om in het bovenste kwart van de scores te staan?

Om deze vraag te beantwoorden, zouden we het derde kwartiel van alle scores vinden, wat de waarde is die de onderste 75% scheidt van de bovenste 25%.

Wat is het interkwartielbereik van een bepaalde dataset?

Het interkwartielbereik (IQR) is het bereik van de middelste 50% van de gegevenswaarden. Om de IQR voor een bepaalde dataset te vinden, kunnen we het derde kwartiel berekenen – het eerste kwartiel.

Aanvullende bronnen

Hoe percentielen in R te berekenen
Hoe kwartielen in R te berekenen
Hoe het interkwartielbereik in Excel te berekenen
Hoe u het interkwartielbereik kunt berekenen op een TI-84-rekenmachine