Phi-coëfficiënt: definitie en voorbeelden

Een Phi-coëfficiënt (ook wel een gemiddelde kwadratische contingentiecoëfficiënt genoemd) is een maatstaf voor de associatie tussen twee binaire variabelen.

Voor een 2×2 tabel gegeven voor twee willekeurige variabelen x en y :

De Phi-coëfficiënt kan als volgt worden berekend:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Voorbeeld: Berekening van een Phi-coëfficiënt

Stel dat we willen weten of gender wel of niet geassocieerd is met de voorkeur voor een politieke partij. We nemen een eenvoudige willekeurige steekproef van 25 kiezers en vragen hen naar hun politieke partijvoorkeur. De volgende tabel geeft de resultaten van het onderzoek weer:

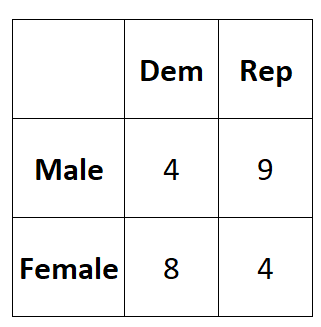
We kunnen de Phi-coëfficiënt tussen de twee variabelen als volgt berekenen:

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0,3589

Opmerking: we hadden dit ook kunnen berekenen met behulp van de Phi-coëfficiëntcalculator.

Hoe een Phi-coëfficiënt te interpreteren

Net als bij een Pearson-correlatiecoëfficiënt, neemt een Phi-coëfficiënt waarden aan tussen -1 en 1 waarbij:

• -1 geeft een volkomen negatieve relatie aan tussen de twee variabelen.
• 0 geeft aan dat er geen verband is tussen de twee variabelen.
• 1 geeft een volkomen positieve relatie aan tussen de twee variabelen.

Over het algemeen geldt dat hoe verder een Phi-coëfficiënt van nul verwijderd is, hoe sterker de relatie tussen de twee variabelen is.

Met andere woorden: hoe verder een Phi-coëfficiënt van nul verwijderd is, hoe meer bewijs er is voor een soort systematisch patroon tussen de twee variabelen.

Aanvullende bronnen

Een gids voor de Pearson-correlatiecoëfficiënt
Een gids voor de Fisher Exact-test
Een gids voor de Chi-kwadraattest van onafhankelijkheid