Hoe een binominale verdeling in r te plotten

Om de waarschijnlijkheidsmassafunctie voor een binominale verdeling in R uit te zetten, kunnen we de volgende functies gebruiken:

• dbinom(x, size, prob) om de waarschijnlijkheidsmassafunctie te creëren
• plot(x, y, type = ‚h‘) om de waarschijnlijkheidsmassafunctie te plotten, waarbij wordt gespecificeerd dat de plot een histogram is (type=’h‘)

Om de waarschijnlijkheidsmassafunctie te plotten, geeft u eenvoudigweg de grootte op   (bijvoorbeeld het aantal pogingen) en prob (bijvoorbeeld de kans op succes bij een bepaalde poging) in de functie dbinom() .

De volgende code illustreert bijvoorbeeld hoe u een waarschijnlijkheidsmassafunctie plot voor een binomiale verdeling met grootte = 20 en waarschijnlijkheid = 0,3:

 success <- 0:20

plot(success, dbinom(success, size=20, prob=.3), type='h')

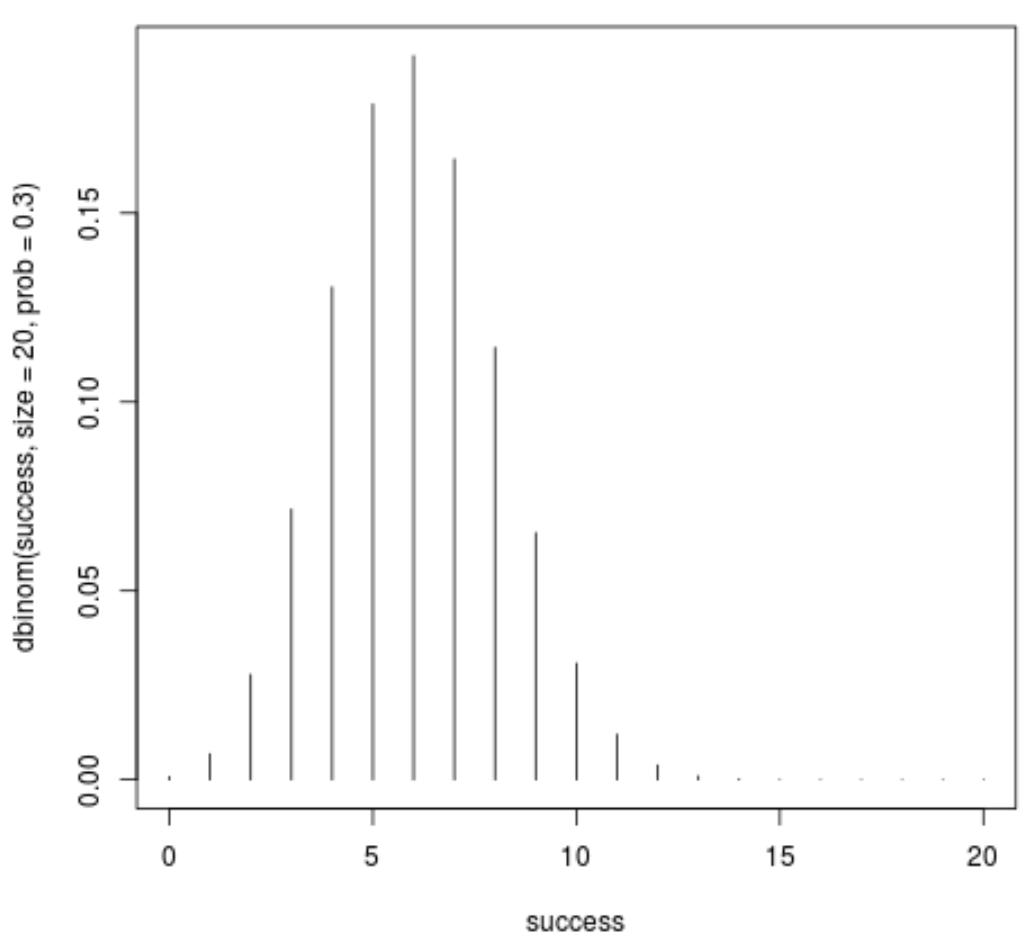
Op de x-as staat het aantal successen en op de y-as de kans op het behalen van dat aantal successen in 20 pogingen.

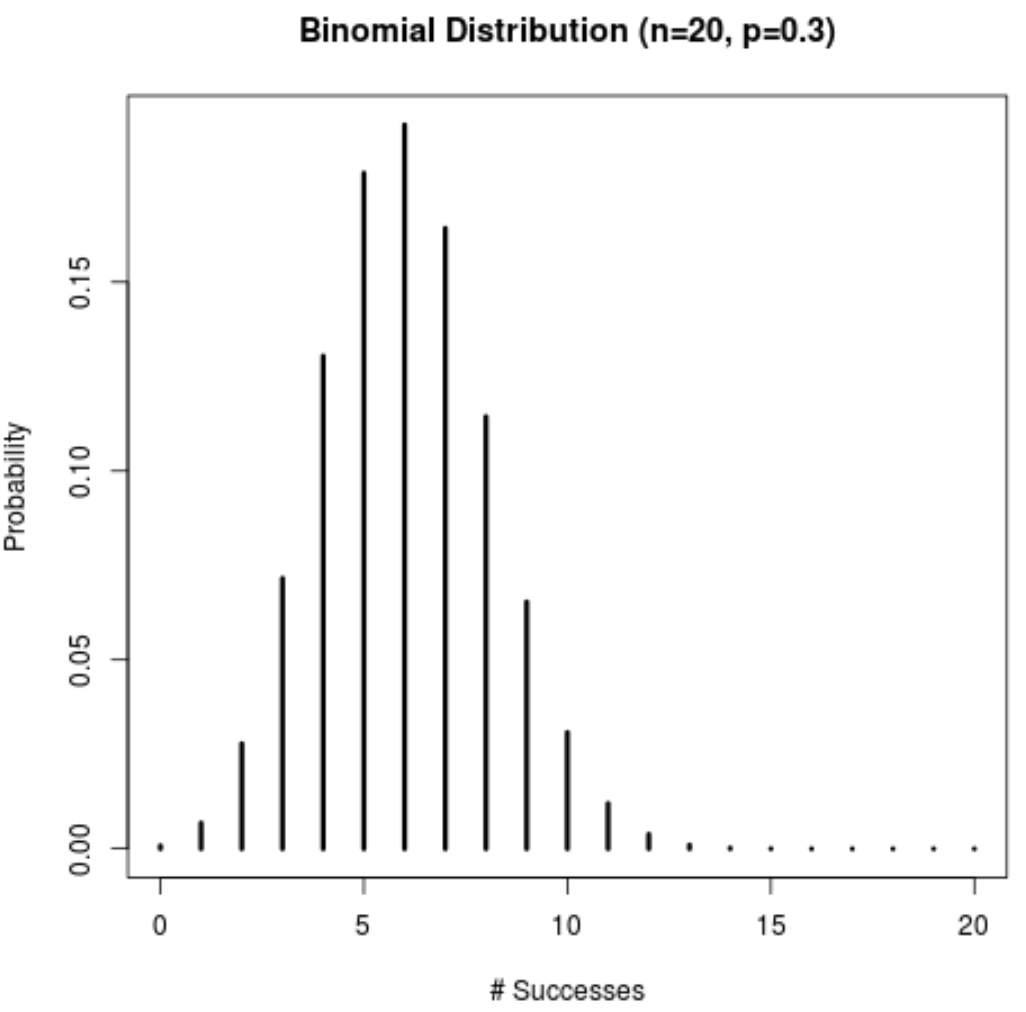
We kunnen een titel toevoegen, de aslabels wijzigen en de breedte van de lijnen vergroten om de plot esthetisch aantrekkelijker te maken:

 success <- 0:20

plot(success,dbinom(success,size=20,prob=.3),
     type='h',
     main='Binomial Distribution (n=20, p=0.3)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

U kunt de volgende code gebruiken om de werkelijke kansen te krijgen voor elk aantal successen dat in de grafiek wordt weergegeven:

 #prevent R from displaying numbers in scientific notation
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dbinom(success, size=20, prob=.3)

[1] 0.00079792266297612 0.00683933711122388 0.02784587252426865
[4] 0.07160367220526231 0.13042097437387065 0.17886305056987975
[7] 0.19163898275344257 0.16426198521723651 0.11439673970486122
[10] 0.06536956554563482 0.03081708090008504 0.01200665489613703
[13] 0.00385928193090119 0.00101783259716075 0.00021810698510587
[16] 0.00003738976887529 0.00000500755833151 0.00000050496386536
[19] 0.00000003606884753 0.00000000162716605 0.00000000003486784

Aanvullende bronnen

Een inleiding tot de binominale verdeling
De vorm van een binominale verdeling begrijpen