Hoe u meerdere lineaire regressieresultaten kunt plotten in r

Wanneer we eenvoudige lineaire regressie in R uitvoeren, is het gemakkelijk om de passende regressielijn te visualiseren, omdat we alleen met een enkele voorspellende variabele en een enkeleresponsvariabele werken.

De volgende code laat bijvoorbeeld zien hoe u een eenvoudig lineair regressiemodel aan een gegevensset kunt aanpassen en de resultaten kunt plotten:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

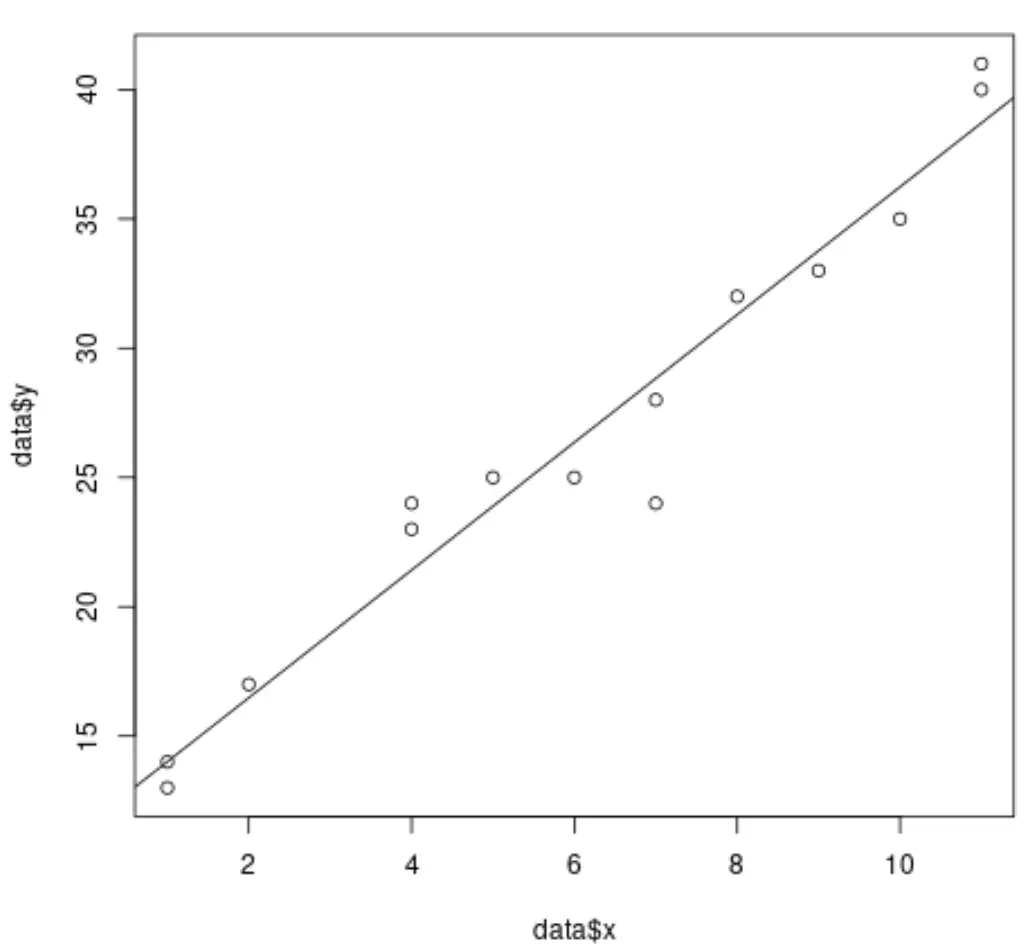
Wanneer we echter meervoudige lineaire regressie uitvoeren, wordt het moeilijk om de resultaten te visualiseren omdat er meerdere voorspellende variabelen zijn en we niet eenvoudigweg een regressielijn in een 2D-grafiek kunnen uitzetten.

In plaats daarvan kunnen we toegevoegde variabele plots gebruiken (ook wel ‚partiële regressieplots‘ genoemd). Dit zijn individuele plots die de relatie weergeven tussen de responsvariabele en een voorspellende variabele, terwijl wordt gecontroleerd voor de aanwezigheid van andere voorspellende variabelen in het model .

Het volgende voorbeeld laat zien hoe u meervoudige lineaire regressie in R uitvoert en de resultaten visualiseert met behulp van bijgevoegde variabele plots.

Voorbeeld: Meerdere lineaire regressieresultaten plotten in R

Stel dat we het volgende meervoudige lineaire regressiemodel passen in een dataset in R met behulp van de ingebouwde mtcars- dataset:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Uit de resultaten kunnen we zien dat de p-waarde voor elk van de coëfficiënten kleiner is dan 0,1. Voor de eenvoud gaan we ervan uit dat elk van de voorspellende variabelen significant is en in het model moet worden opgenomen.

Om plots van toegevoegde variabelen te produceren, kunnen we de functie avPlots() uit het car- pakket gebruiken:

 #load car package
library(car)

#produce added variable plots
avPlots(model)

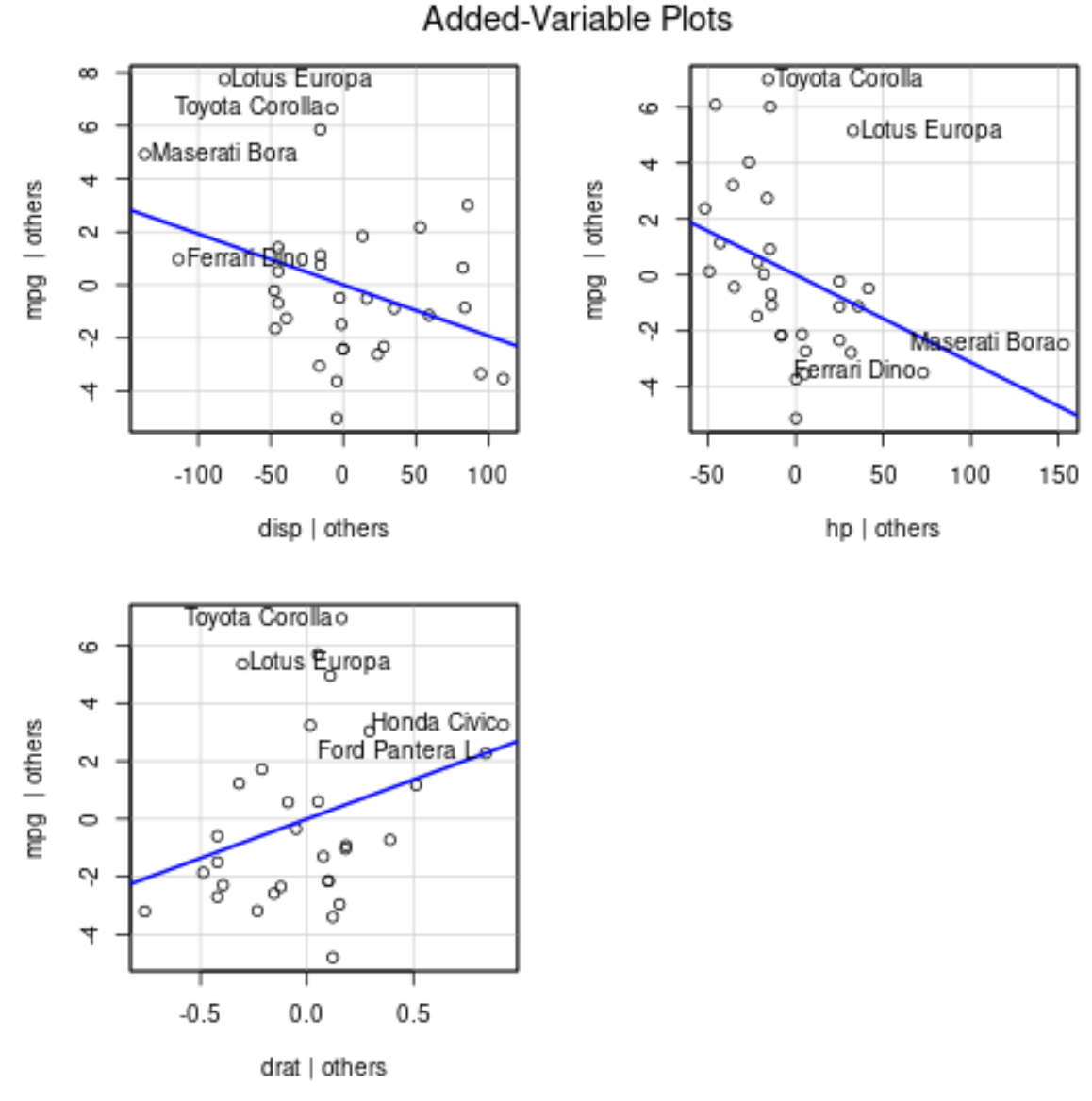
Zo interpreteer je elk plot:

• Op de x-as wordt een enkele voorspellende variabele weergegeven en op de y-as de responsvariabele.
• De blauwe lijn toont het verband tussen de voorspellende variabele en de responsvariabele, terwijl de waarde van alle andere voorspellende variabelen constant wordt gehouden .
• De gelabelde punten in elke grafiek vertegenwoordigen de twee waarnemingen met de grootste residuen en de twee waarnemingen met de grootste gedeeltelijke invloed.

Merk op dat de hoek van de lijn in elke grafiek overeenkomt met het teken van de coëfficiënt van de geschatte regressievergelijking.

Hier volgen bijvoorbeeld de geschatte coëfficiënten voor elke voorspellende variabele in het model:

• weergave: -0,019232
• ch: -0,031229
• datum: 2.714975

Merk op dat de hoek van de lijn positief is in de toegevoegde variabele grafiek voor drat , terwijl deze negatief is voor disp en hp , wat overeenkomt met de tekens van hun geschatte coëfficiënten:

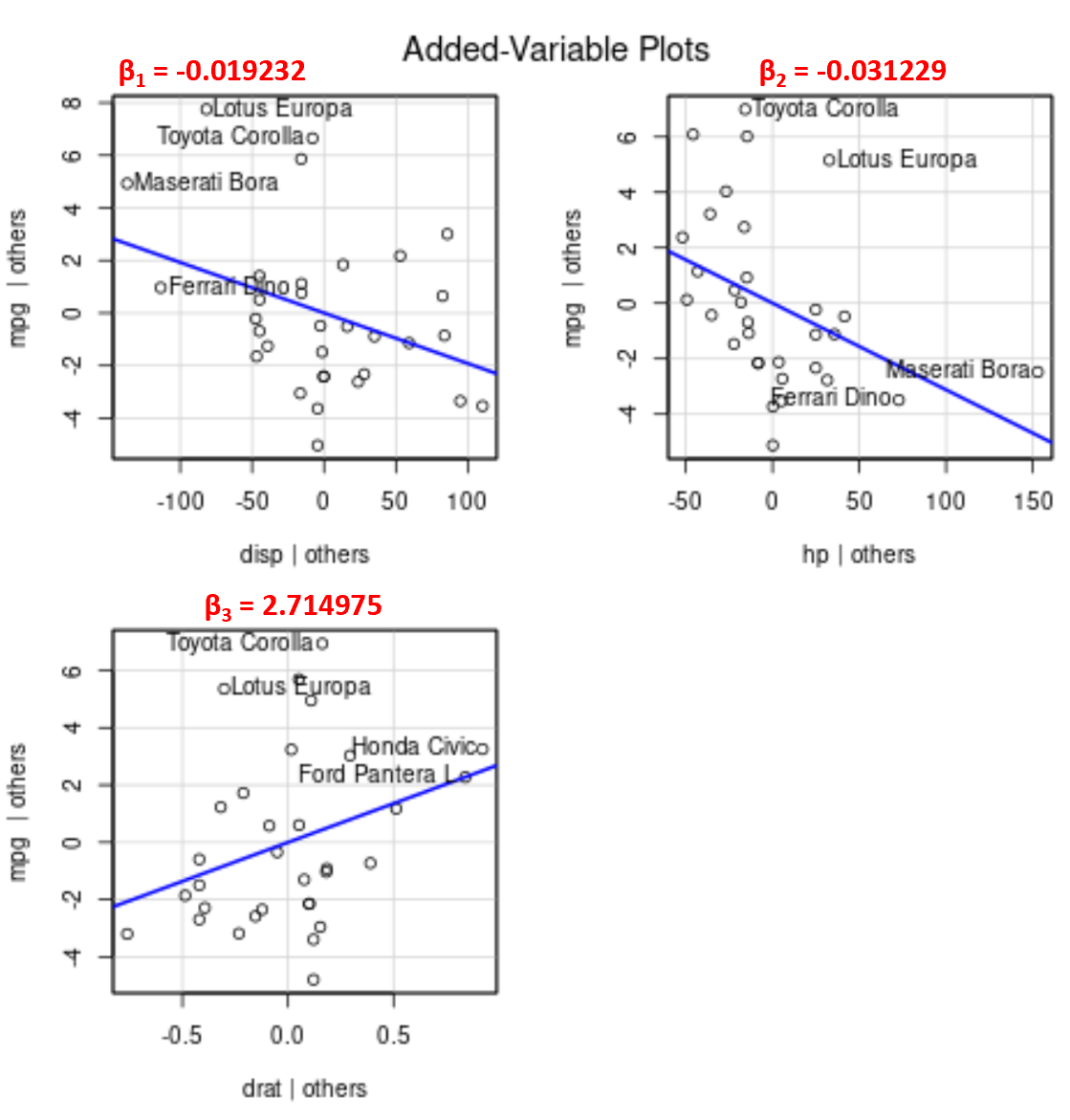
Hoewel we geen enkele aangepaste regressielijn in een 2D-grafiek kunnen uitzetten, omdat we meerdere voorspellende variabelen hebben, stellen deze toegevoegde variabelegrafieken ons in staat de relatie tussen elke individuele voorspellende variabele en de responsvariabele te observeren terwijl we de andere voorspellende variabelen constant houden.