Wat is een waarschijnlijkheidsmassafunctie (pmf) in de statistiek?

Een waarschijnlijkheidsmassafunctie , vaak afgekort PMF , vertelt ons de waarschijnlijkheid dat een discrete willekeurige variabele een bepaalde waarde aanneemt.

Stel bijvoorbeeld dat we één keer met een dobbelsteen gooien. Als we x het nummer laten aangeven waarop de dobbelsteen terechtkomt, dan kan de kans dat x gelijk is aan verschillende waarden als volgt worden beschreven:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Er is een gelijke kans dat de dobbelstenen op een willekeurig getal tussen 1 en 6 terechtkomen.

Hier ziet u hoe we deze kansen zouden schrijven als een waarschijnlijkheidsmassafunctie:

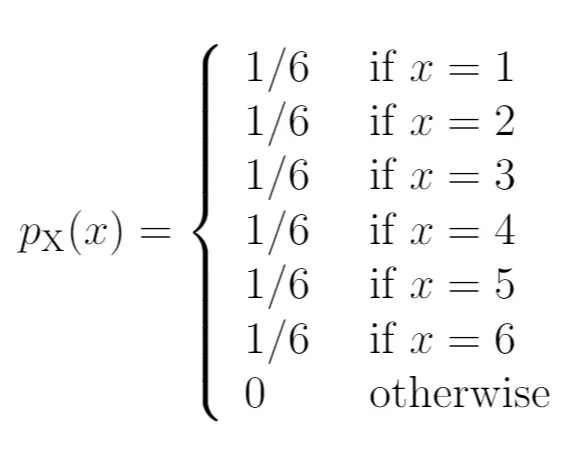
De linkerkant van het diagram toont de waarschijnlijkheid die verband houdt met de uitkomsten aan de rechterkant:

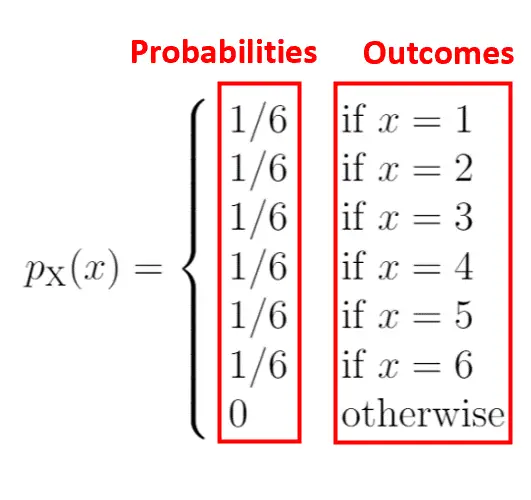
Een kenmerk van een waarschijnlijkheidsmassafunctie is dat alle kansen opgeteld tot 1 moeten komen. U zult merken dat deze PMF aan deze voorwaarde voldoet:

Som van kansen = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Ondersteuning voor een waarschijnlijkheidsmassafunctie verwijst naar de reeks waarden die de discrete willekeurige variabele kan aannemen. In dit voorbeeld zou de steun {1, 2, 3, 4, 5, 6} zijn, aangezien de waarde van de dobbelsteen elk van deze waarden kan aannemen.

Buiten de ondersteuning is de PMF-waarde nul. De kans dat de dobbelsteen op “0” of “7” of “8” terechtkomt, is bijvoorbeeld nul, aangezien geen van deze getallen in het haakje staat.

Waarschijnlijkheidsmassafuncties in de praktijk

De twee meest voorkomende voorbeelden van waarschijnlijkheidsmassafuncties in de praktijk betreffen de binominale verdeling en de Poisson-verdeling .

Binomiale verdeling

Als een willekeurige variabele X een binominale verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Goud:

• n: aantal pogingen
• k: aantal successen
• p: kans op succes bij een bepaalde proef
• _n C _k : het aantal manieren om k successen te behalen in n pogingen

Stel dat we bijvoorbeeld drie keer een munt opgooien. We kunnen de bovenstaande formule gebruiken om de kans te bepalen op het krijgen van 0, 1, 2 en 3 kop bij deze 3 worpen:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Vis distributie

Als een willekeurige variabele X een Poisson-verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = λ ^k * e ^{– λ} / k!

Goud:

• λ: gemiddeld aantal successen dat optreedt tijdens een specifiek interval
• k: aantal successen
• e: een constante gelijk aan ongeveer 2,71828

Stel bijvoorbeeld dat in een bepaald ziekenhuis gemiddeld twee geboorten per uur plaatsvinden. We kunnen de bovenstaande formule gebruiken om de waarschijnlijkheid van 0, 1, 2, 3 geboorten, enz. te bepalen. in een bepaald uur:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Bekijk een PMF

We visualiseren waarschijnlijkheidsmassafuncties vaak met staafdiagrammen.

Het volgende staafdiagram toont bijvoorbeeld de kansen die verband houden met het aantal geboorten per uur voor de Poisson-verdeling die in het vorige voorbeeld is beschreven:

Merk op dat het aantal geboorten zich tot in het oneindige kan uitstrekken, maar de kansen worden na 10 zo klein dat je ze niet eens in een staafdiagram kunt zien.

Eigenschappen van een PMF

Een waarschijnlijkheidsmassafunctie heeft de volgende eigenschappen:

1. Alle kansen zijn positief ter ondersteuning. De kans dat een dobbelsteen tussen 1 en 6 valt, is bijvoorbeeld positief, terwijl de kans op alle andere uitkomsten nul is.

2. Alle uitkomsten hebben een waarschijnlijkheid tussen 0 en 1. De kans dat een dobbelsteen tussen 1 en 6 valt, is bijvoorbeeld 1/6, of 0,1666666 voor elke uitkomst.

3. De som van alle kansen moet gelijk zijn aan 1. De som van de kansen dat een dobbelsteen op een bepaald getal valt, is bijvoorbeeld 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Aanvullende bronnen

Wat zijn willekeurige variabelen?
CDF of PDF: wat is het verschil?
Een inleiding tot de binominale verdeling
Een inleiding tot de Poisson-verdeling