Een poisson-betrouwbaarheidsinterval berekenen (stap voor stap)

De Poisson-verdeling is een waarschijnlijkheidsverdeling die wordt gebruikt om de waarschijnlijkheid te modelleren dat een bepaald aantal gebeurtenissen plaatsvindt tijdens een vast tijdsinterval, wanneer bekend is dat de gebeurtenissen onafhankelijk en met een constante gemiddelde snelheid plaatsvinden.

Hoewel het nuttig is om het gemiddelde aantal keren dat een Poisson-proces voorkomt te kennen, kan het nog nuttiger zijn om een betrouwbaarheidsinterval rond het gemiddelde aantal keren te hebben.

Laten we bijvoorbeeld zeggen dat we op een willekeurige dag gegevens verzamelen bij een callcenter en zien dat het gemiddelde aantal oproepen per uur 15 is.

Omdat we de gegevens slechts voor één dag hebben verzameld, kunnen we er niet zeker van zijn dat het callcenter het hele jaar door gemiddeld 15 oproepen per uur ontvangt.

We kunnen echter de volgende formule gebruiken om een betrouwbaarheidsinterval te berekenen voor het gemiddelde aantal oproepen per uur:

Poisson-betrouwbaarheidsintervalformule

Betrouwbaarheidsinterval = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

Goud:

• X ² : Kritische waarde van chikwadraat
• N: Het aantal waargenomen gebeurtenissen
• α: het significantieniveau

Het volgende stapsgewijze voorbeeld illustreert hoe u in de praktijk een 95% Poisson-betrouwbaarheidsinterval kunt berekenen.

Stap 1: tel de waargenomen gebeurtenissen

Stel dat we berekenen dat het gemiddelde aantal oproepen per uur in een callcenter 15 is. Dus N = 15 .

En aangezien we een betrouwbaarheidsinterval van 95% berekenen, gebruiken we α = 0,05 in de volgende berekeningen.

Stap 2: Zoek de ondergrens van het betrouwbaarheidsinterval

De ondergrens van het betrouwbaarheidsinterval wordt als volgt berekend:

• Ondergrens = 0,5*X ² _{2N, α/2}
• Ondergrens = 0,5*X ² _{2(15), 0,975}
• Ondergrens = 0,5*X ² _{30, 0,975}
• Ondergrens = 0,5*16,791
• Ondergrens = 8,40

Opmerking: We hebben de chikwadraat-calculator voor kritische waarden gebruikt om X ² _{30, 0,975} te berekenen.

Stap 3: Zoek de bovengrens van het betrouwbaarheidsinterval

De bovengrens van het betrouwbaarheidsinterval wordt als volgt berekend:

• Bovengrens = 0,5*X ² _{2(N+1), 1-α/2}
• Bovengrens = 0,5*X ² _{2(15+1), 0,025}
• Bovengrens = 0,5*X ² _{32, 0,025}
• Bovengrens = 0,5*49,48
• Bovengrens = 24,74

Opmerking: We hebben de chikwadraat-calculator voor kritische waarden gebruikt om X ² _32.0.025 te berekenen.

Stap 4: Vind het betrouwbaarheidsinterval

Met behulp van de eerder berekende onder- en bovengrenzen blijkt ons 95% Poisson-betrouwbaarheidsinterval:

• 95% BI = [8,40; 24,74]

Dit betekent dat we er 95% zeker van zijn dat het daadwerkelijke gemiddelde aantal oproepen per uur dat het callcenter ontvangt tussen de 8,40 oproepen en 24,74 oproepen ligt.

Bonus: Fish Confidence Interval Calculator

Voel je vrij om deze Poisson-betrouwbaarheidsintervalcalculator te gebruiken om automatisch een Poisson-betrouwbaarheidsinterval te berekenen.

Zo kunt u deze rekenmachine bijvoorbeeld als volgt gebruiken om het Poisson-betrouwbaarheidsinterval te vinden dat we zojuist handmatig hebben berekend:

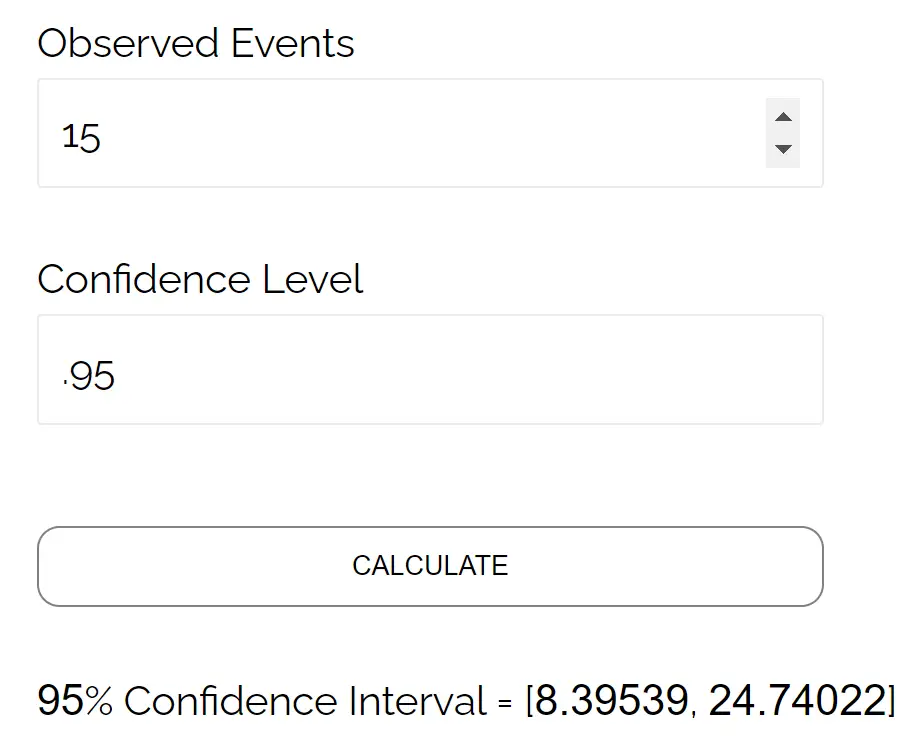
Merk op dat de resultaten overeenkomen met het betrouwbaarheidsinterval dat we handmatig hebben berekend.