Polynomiale regressie

Von Dr.benjamin anderson August 2, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat polynomiale regressie in de statistiek is en hoe deze wordt uitgevoerd. Bovendien kunt u een voorbeeld zien waarin een polynomiale regressie wordt uitgevoerd.

Wat is polynomiale regressie?

Polynomiale regressie , of polynomiale regressie , is een regressiemodel waarin de relatie tussen de onafhankelijke variabele X en de afhankelijke variabele Y wordt gemodelleerd met behulp van een polynoom.

De vergelijking voor een kwadratisch polynoomregressiemodel is bijvoorbeeld y=β ₀ +β ₁ x+β ₂ x ² +ε.

Polynomiale regressie is handig voor het aanpassen van gegevenssets waarvan de grafieken polynomiale curven zijn. Dus als de puntenplot van een gegevensmonster de vorm heeft van een parabool, is het beter om een kwadratisch regressiemodel te construeren in plaats van een lineair regressiemodel. Op deze manier zal de regressiemodelvergelijking beter bij het gegevensmonster passen.

Merk op dat polynomiale regressie een soort niet-lineaire regressie is, net als exponentiële regressie en logaritmische regressie.

Polynomiale regressieformule

De vergelijking voor een polynoom regressiemodel is y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Goud:

$y$

is de afhankelijke variabele.
$x$

is de onafhankelijke variabele.
$\beta_0$

is de constante van de polynomiale regressievergelijking.
$\beta_i$

is de regressiecoëfficiënt die aan de variabele is gekoppeld

$x^i$

.
$\bm{\varepsilon}$

Dit is de fout of het residu, dat wil zeggen het verschil tussen de waargenomen waarde en de door het model geschatte waarde.

Dus als we een monster hebben met een totaal van

$n$

observaties kunnen we het polynomiale regressiemodel in matrixvorm voorstellen:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

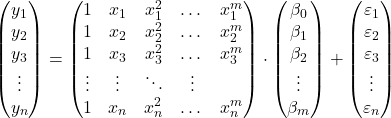
De bovenstaande matrixuitdrukking kan worden herschreven door aan elke matrix een letter toe te wijzen:

$Y=X\beta+\varepsilon$

Door het kleinste kwadratencriterium toe te passen, kunnen we dus tot de formule komen voor het schatten van de coëfficiënten van een polynoomregressiemodel :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Het handmatig uitvoeren van deze berekeningen is echter erg bewerkelijk en tijdrovend, dus het is handiger om computersoftware (zoals Minitab of Excel) te gebruiken waarmee u veel sneller een polynoomregressiemodel kunt uitvoeren.

Voorbeeld van een polynoomregressiemodel

Nu we de definitie van polynomiale regressie kennen en hoe deze wordt uitgevoerd, gaan we naar een voorbeeld uit de praktijk kijken om het concept volledig te begrijpen.

Allereerst moet in gedachten worden gehouden dat een polynoomregressiemodel moet worden uitgevoerd wanneer de gegevensgrafiek de vorm heeft van een polynomiale curve. Als de dotplot bijvoorbeeld de vorm heeft van een kubieke curve, moeten we een polynoomregressiemodel van de derde graad construeren.

Zoals u in de volgende afbeelding ziet, heeft het puntendiagram van onze gegevens een kwadratische vorm, omdat naarmate we de waarde van de onafhankelijke variabele verhogen, de afhankelijke variabele sneller groeit. In dit geval werd een lineair regressiemodel uitgevoerd en zoals je kunt zien past dit niet goed bij de punten, omdat het secties heeft waarin de lijn onder alle punten ligt en secties waarin de lijn erboven ligt.

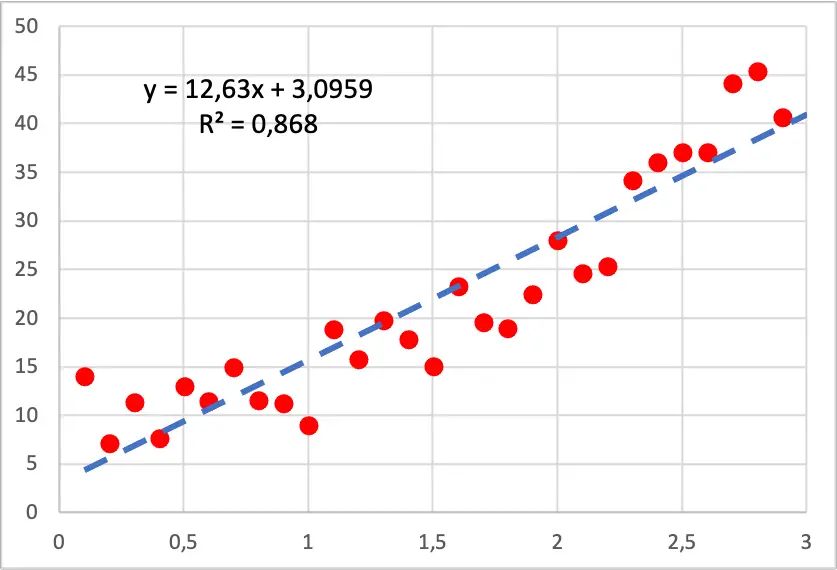
Aan de andere kant, als we een kwadratisch polynoomregressiemodel uitvoeren, past dit veel beter bij de voorbeeldgegevens, zoals u kunt zien in de onderstaande afbeelding.

Bovendien verbetert bij het ontwikkelen van een polynoomregressiemodel de determinatiecoëfficiënt aanzienlijk, aangezien deze van 86,80% naar 94,05% gaat. Daarom verklaart het nieuwe regressiemodel de dataset veel beter.

Aan de andere kant is een andere indicatie dat we polynomiale regressie moeten uitvoeren het plotten van residuen. Als bij een lineaire regressie de grafiek van de residuen de vorm heeft van een parabool of een ander type polynoom, past een polynoomregressiemodel zeker beter bij de bestudeerde gegevens.

Andere soorten niet-lineaire regressie

Er zijn hoofdzakelijk drie soorten niet-lineaire regressie:

Polynoomregressie – De regressiemodelvergelijking heeft de vorm van een polynoom.
Logaritmische regressie : de logaritme van de onafhankelijke variabele wordt genomen.
Exponentiële regressie : de onafhankelijke variabele wordt gevonden in de exponent van de vergelijking.

➤ Zie: Logaritmische regressie
➤ Zie: Exponentiële regressie

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder