Hoe polynomiale regressie uit te voeren in excel

Regressieanalyse wordt gebruikt om de relatie tussen een of meer verklarende variabelen en een responsvariabele te kwantificeren.

Het meest voorkomende type regressieanalyse iseenvoudige lineaire regressie , die wordt gebruikt wanneer een verklarende variabele en een responsvariabele een lineair verband hebben.

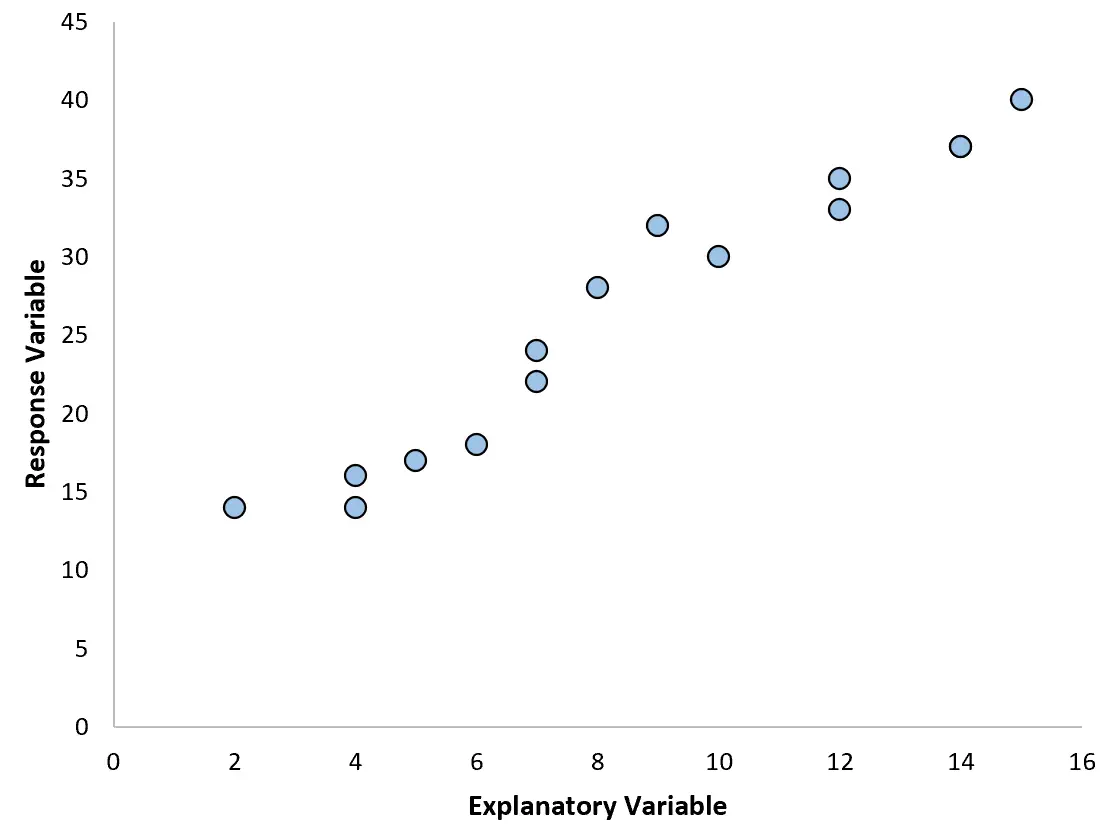
Soms is de relatie tussen een verklarende variabele en een responsvariabele echter niet-lineair.

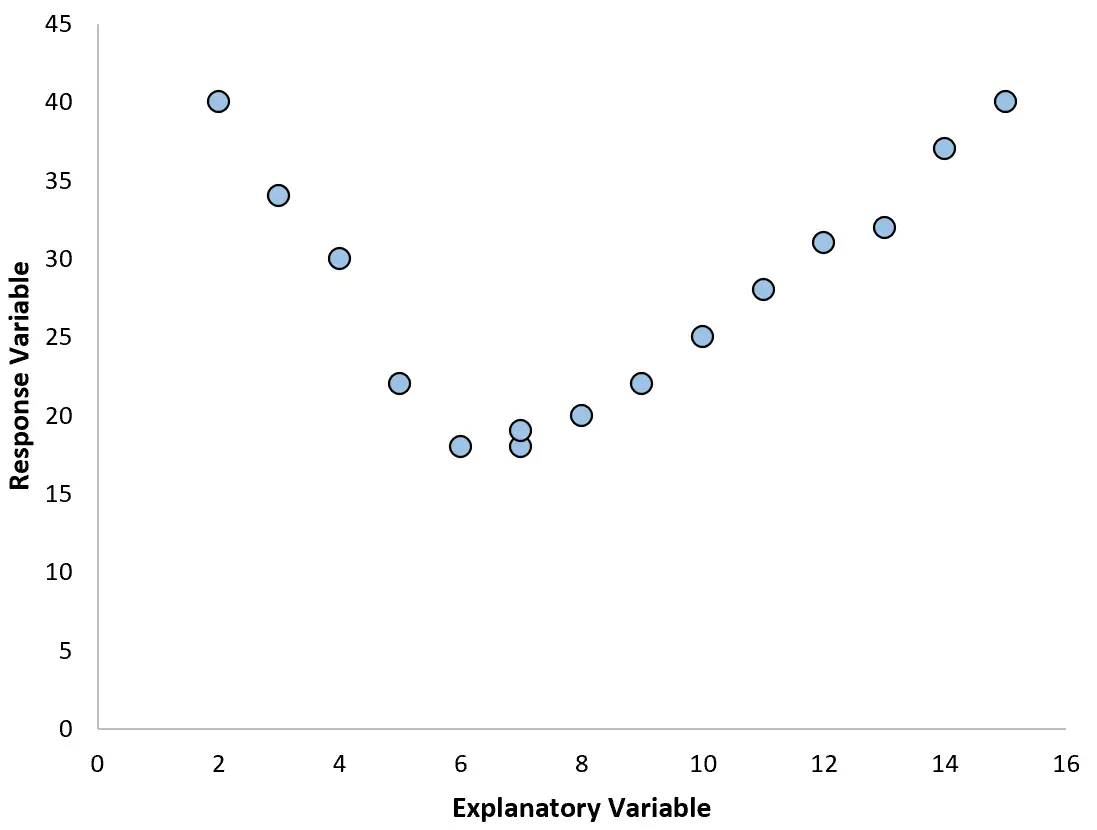
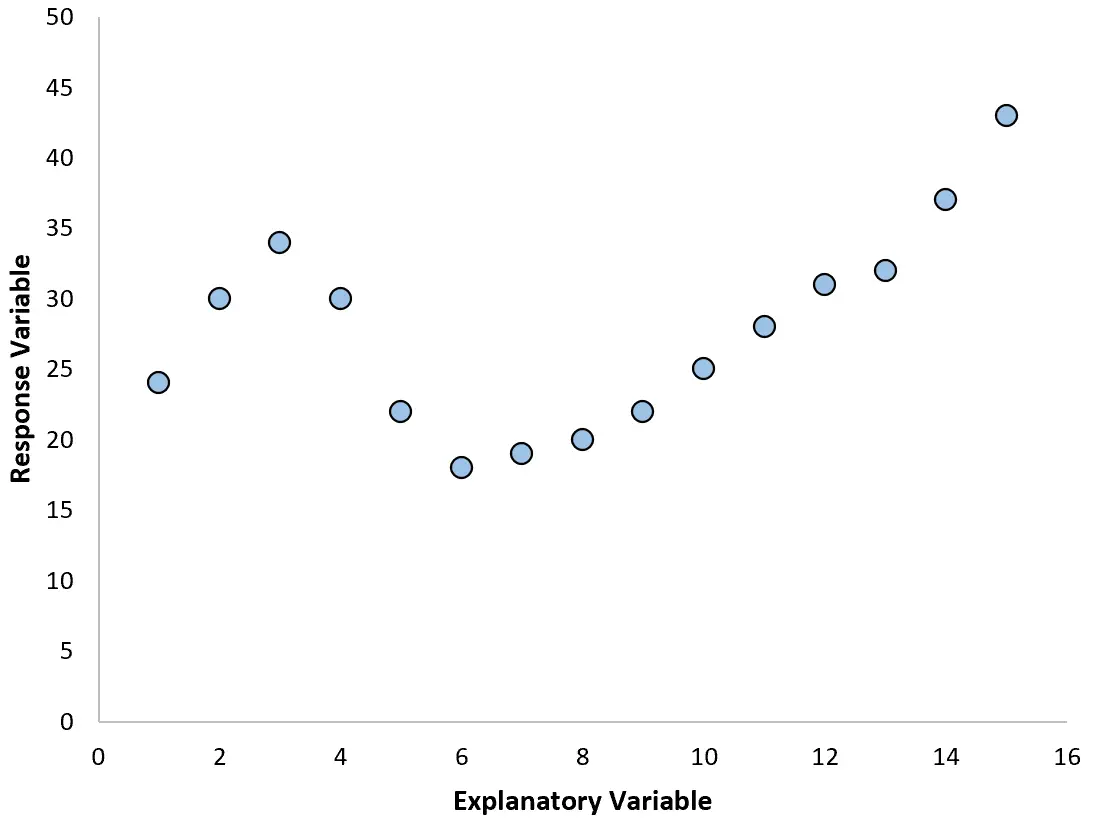
In deze gevallen is het zinvol om polynomiale regressie te gebruiken, die de niet-lineaire relatie tussen variabelen kan verklaren.

In deze zelfstudie wordt uitgelegd hoe u polynomiale regressie uitvoert in Excel.

Voorbeeld: polynomiale regressie in Excel

Stel dat we de volgende gegevensset in Excel hebben:

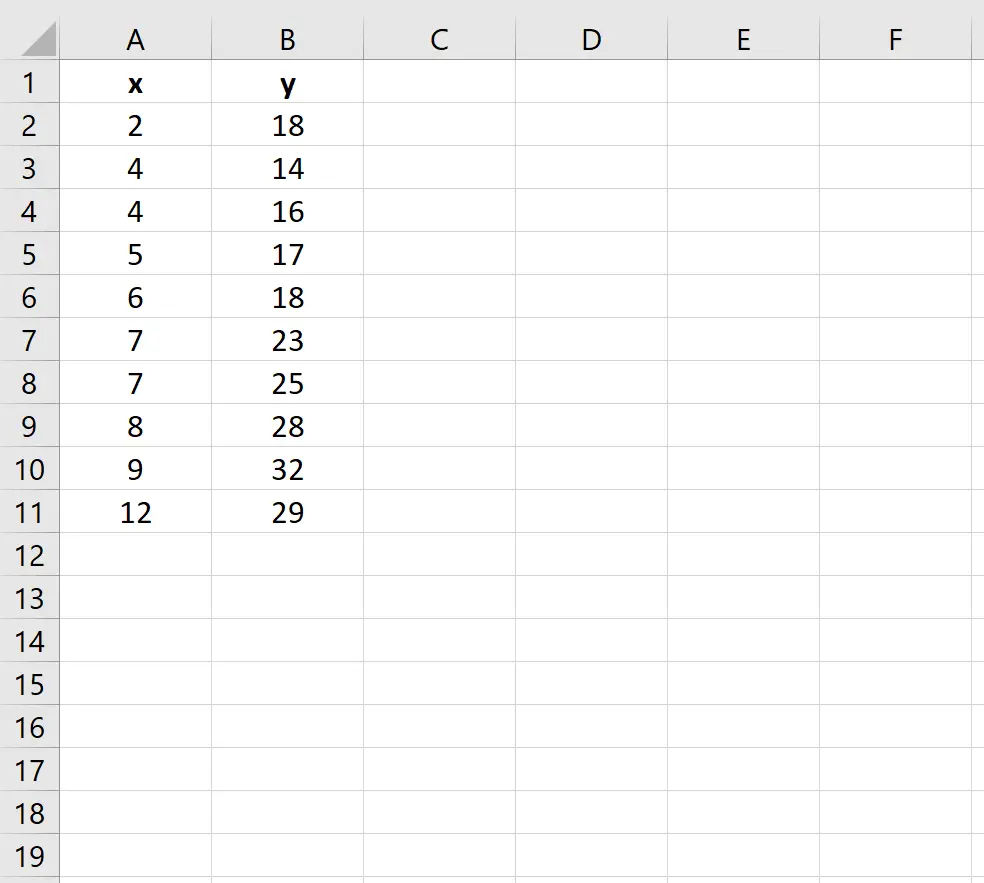
Voer de volgende stappen uit om een polynomiale regressievergelijking aan deze gegevensset toe te passen:

Stap 1: Maak een spreidingsdiagram.

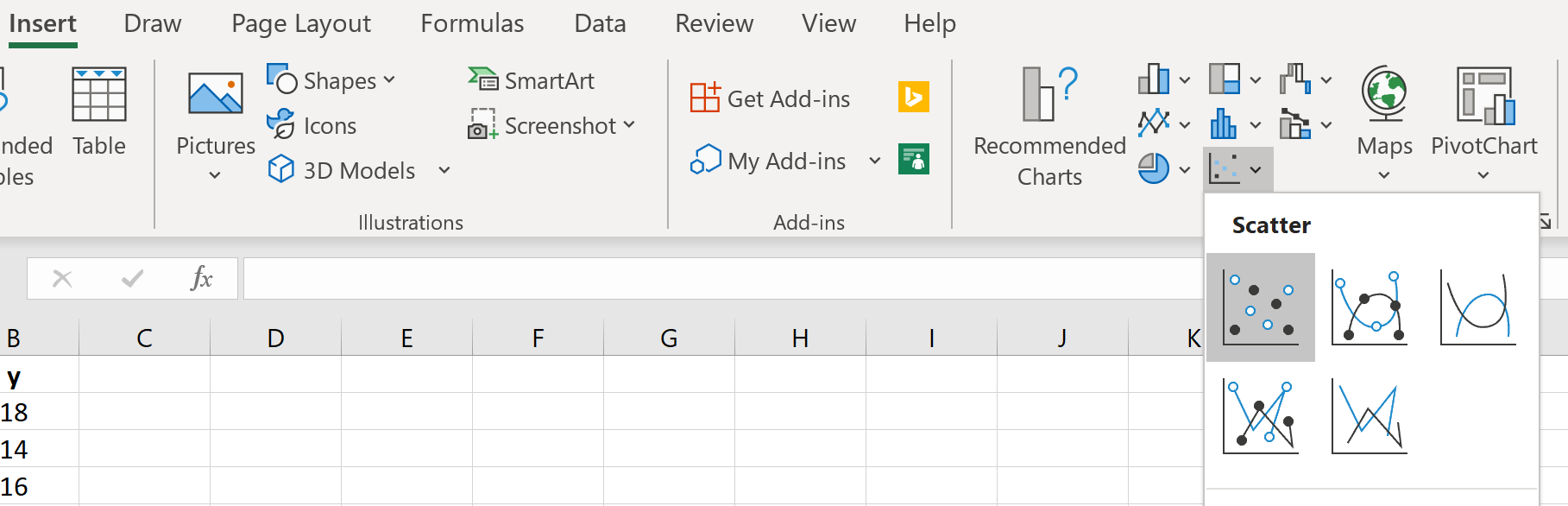
Eerst moeten we een spreidingsdiagram maken. Ga naar de groep Grafieken op het tabblad Invoegen en klik op het eerste grafiektype in Spreiding :

Er verschijnt automatisch een puntenwolk:

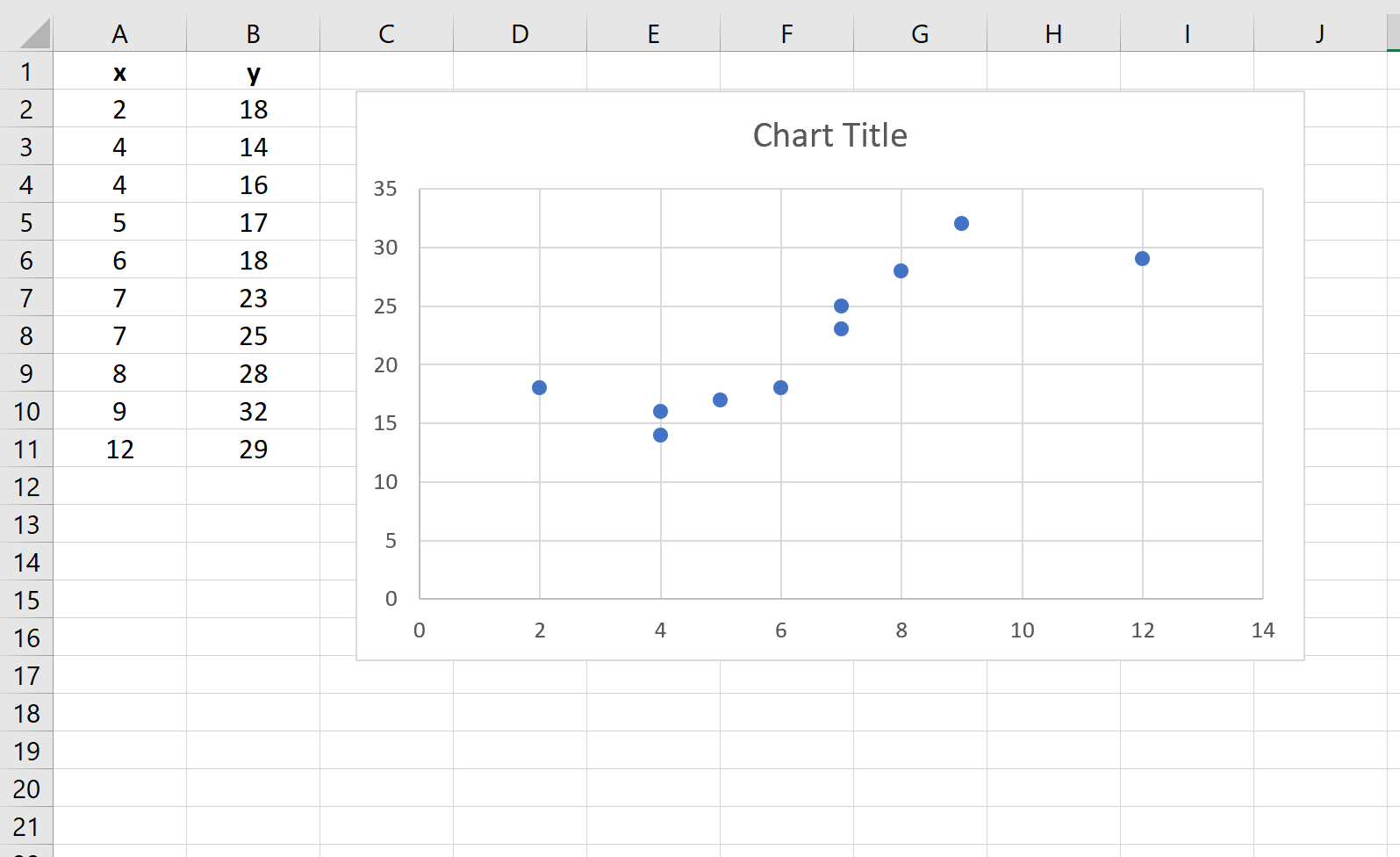
Stap 2: Voeg een trendlijn toe.

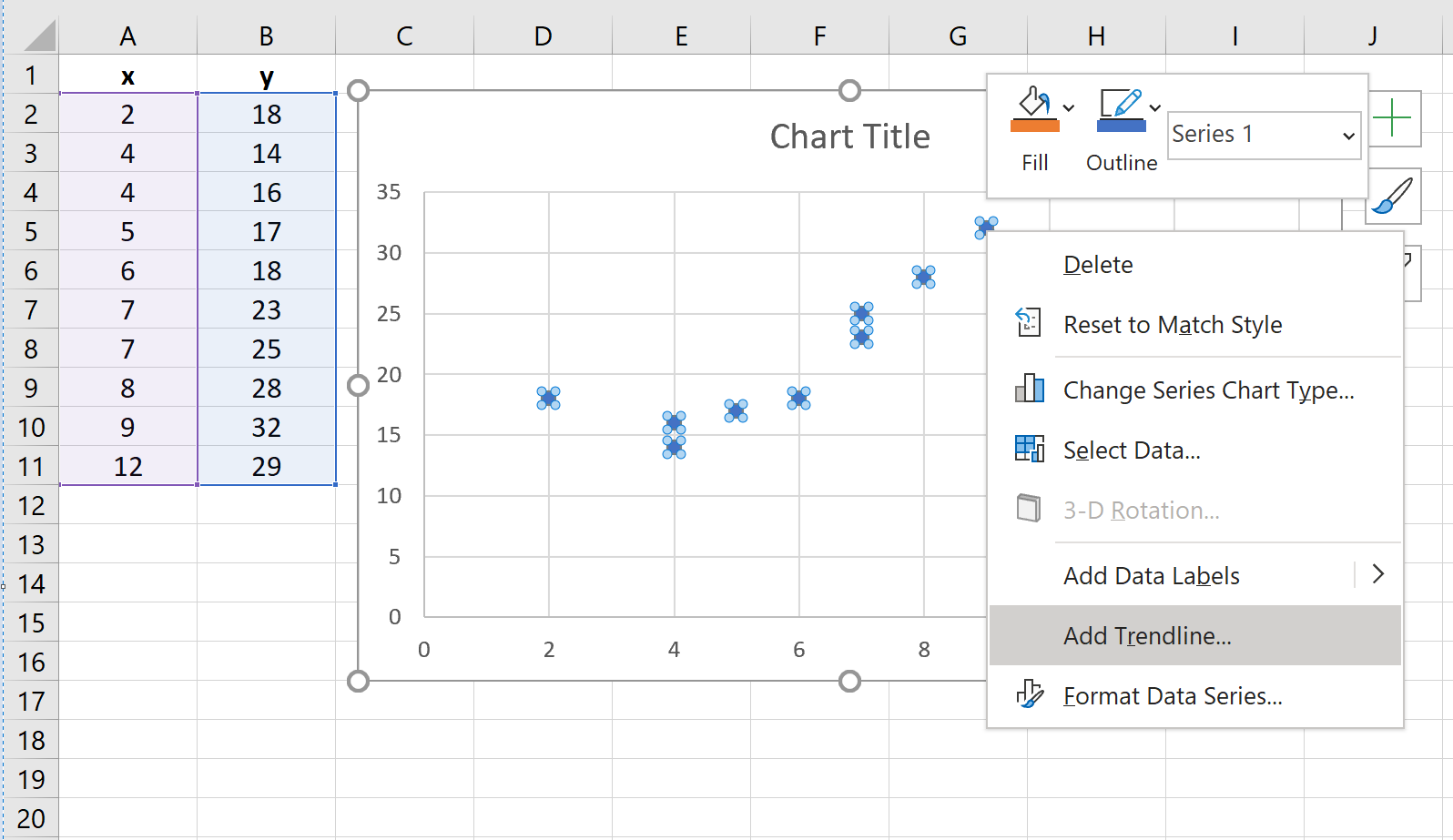
Vervolgens moeten we een trendlijn aan het spreidingsdiagram toevoegen. Klik hiervoor op een van de afzonderlijke punten in de puntenwolk. Klik vervolgens met de rechtermuisknop en selecteer Trendlijn toevoegen…

Er verschijnt een nieuw venster met de optie om een trendlijn op te geven. Kies Polynomial en kies het nummer dat u wilt gebruiken voor Order . We gebruiken 3. Vink vervolgens het vakje onderaan aan met de tekst Toon vergelijking in grafiek .

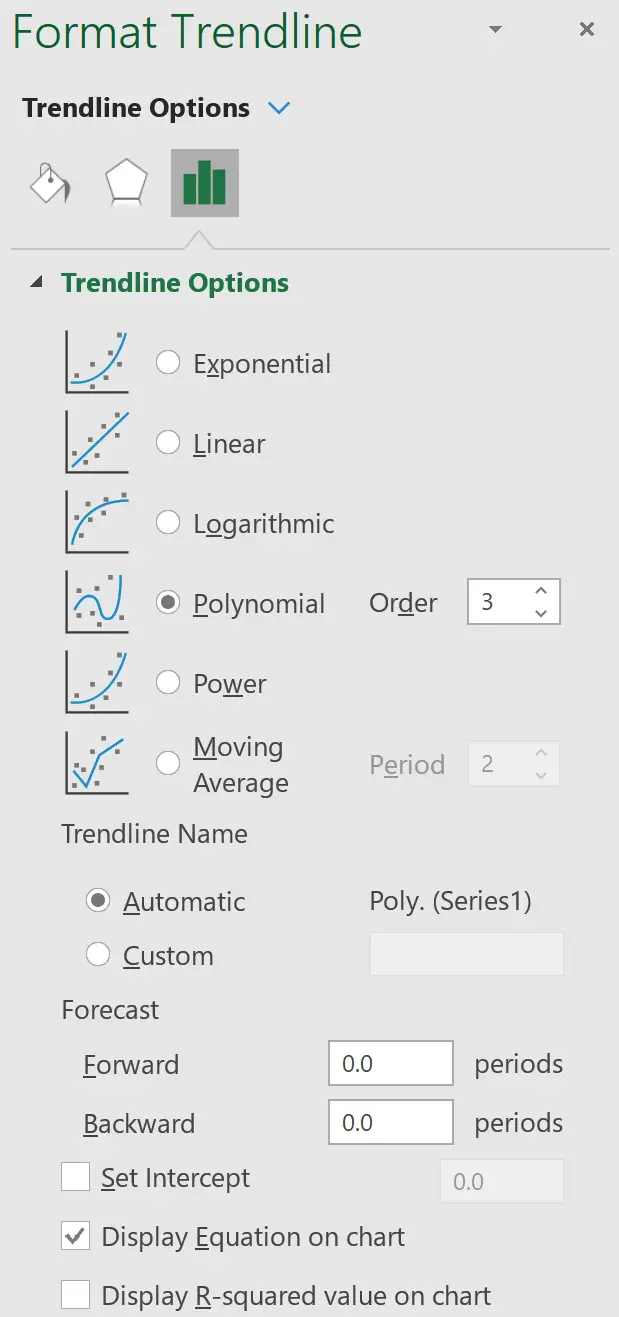
Er verschijnt automatisch een trendlijn met een polynomiale regressievergelijking op het spreidingsdiagram:

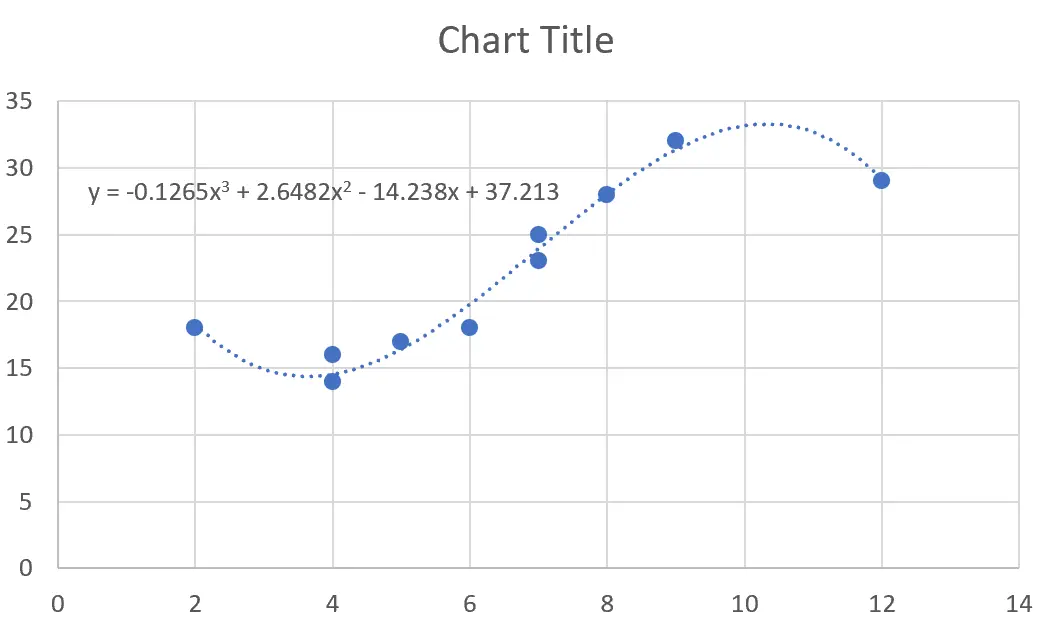
Stap 3: Interpreteer de regressievergelijking.

Voor dit specifieke voorbeeld is onze aangepaste polynomiale regressievergelijking:

y = -0,1265x ³ + 2,6482x ² – 14,238x + 37,213

Deze vergelijking kan worden gebruikt om de verwachte waarde van de responsvariabele te vinden, gegeven een gegeven waarde van de verklarende variabele. Stel bijvoorbeeld dat x = 4. De verwachte waarde voor de responsvariabele, y, zou zijn:

y = -0,1265(4) ³ + 2,6482(4) ² – 14,238(4) + 37,213 = 14,5362 .