Polynomiale regressie in google spreadsheets (stap voor stap)

Regressieanalyse wordt gebruikt om de relatie tussen een of meer voorspellende variabelen en een responsvariabele te kwantificeren.

Het meest voorkomende type regressieanalyse iseenvoudige lineaire regressie , die wordt gebruikt wanneer een voorspellende variabele en een responsvariabele een lineair verband hebben.

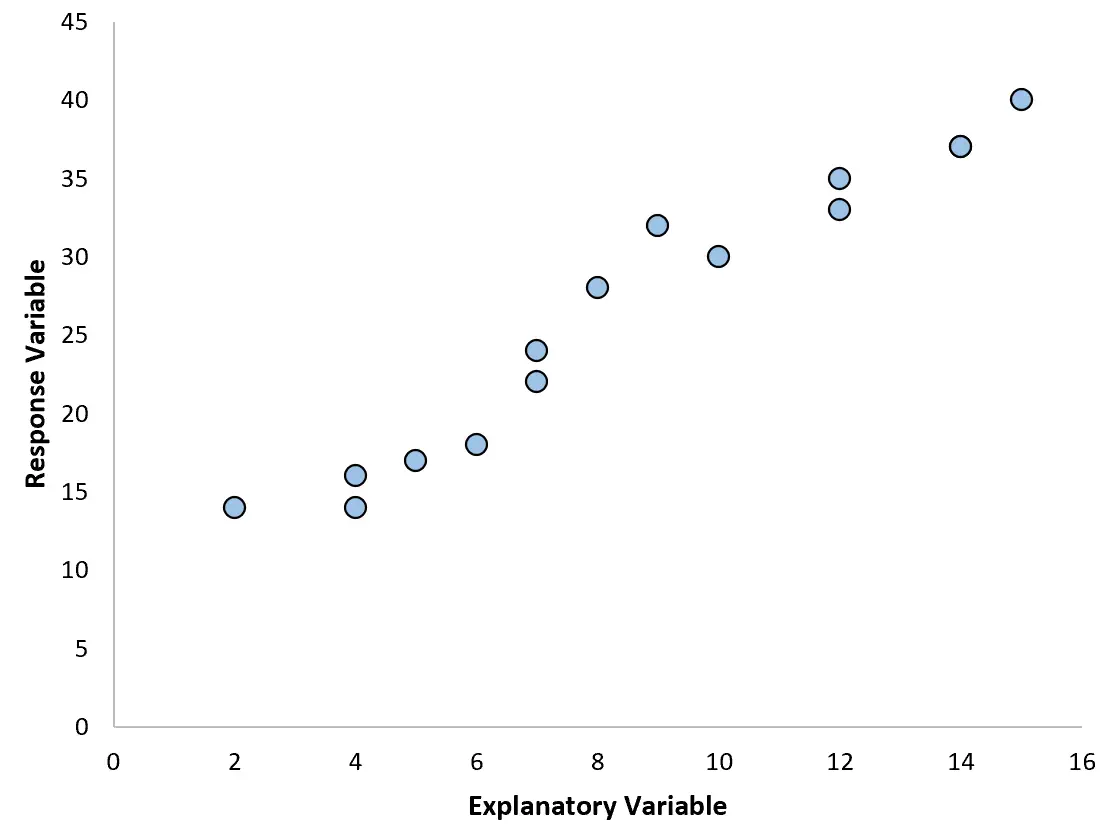
Soms is de relatie tussen een voorspellende variabele en een responsvariabele echter niet-lineair.

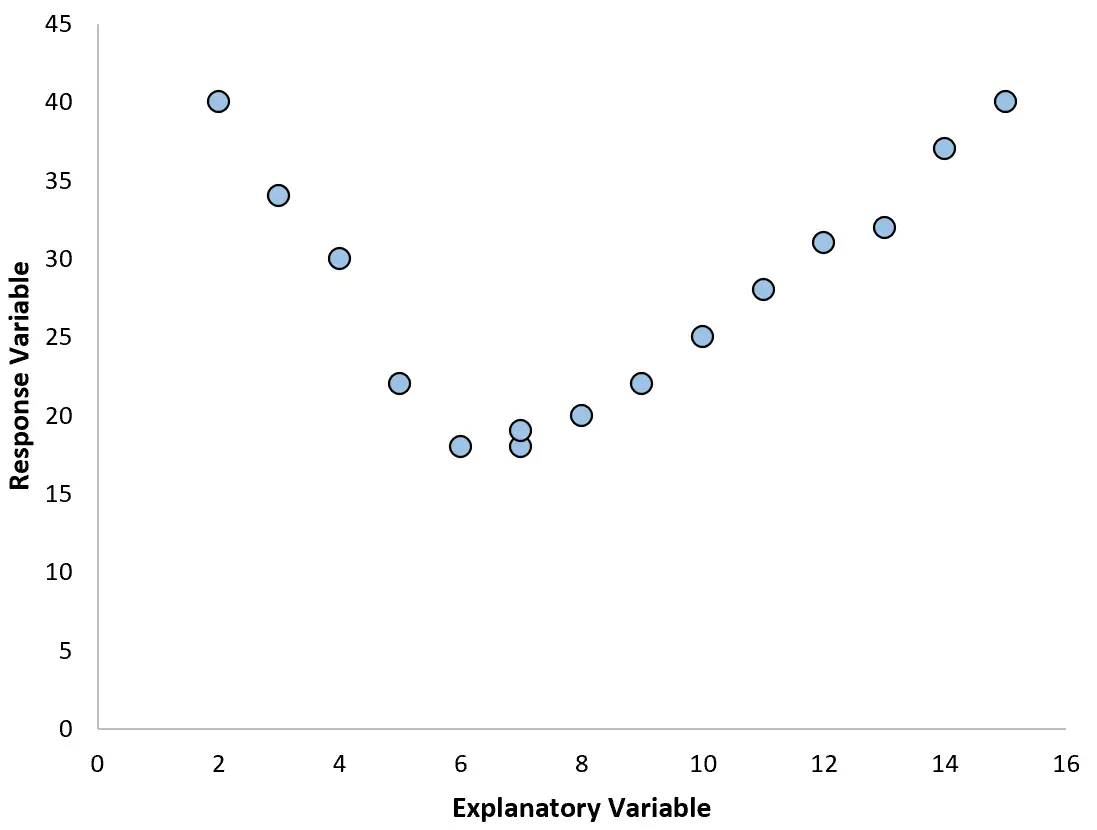
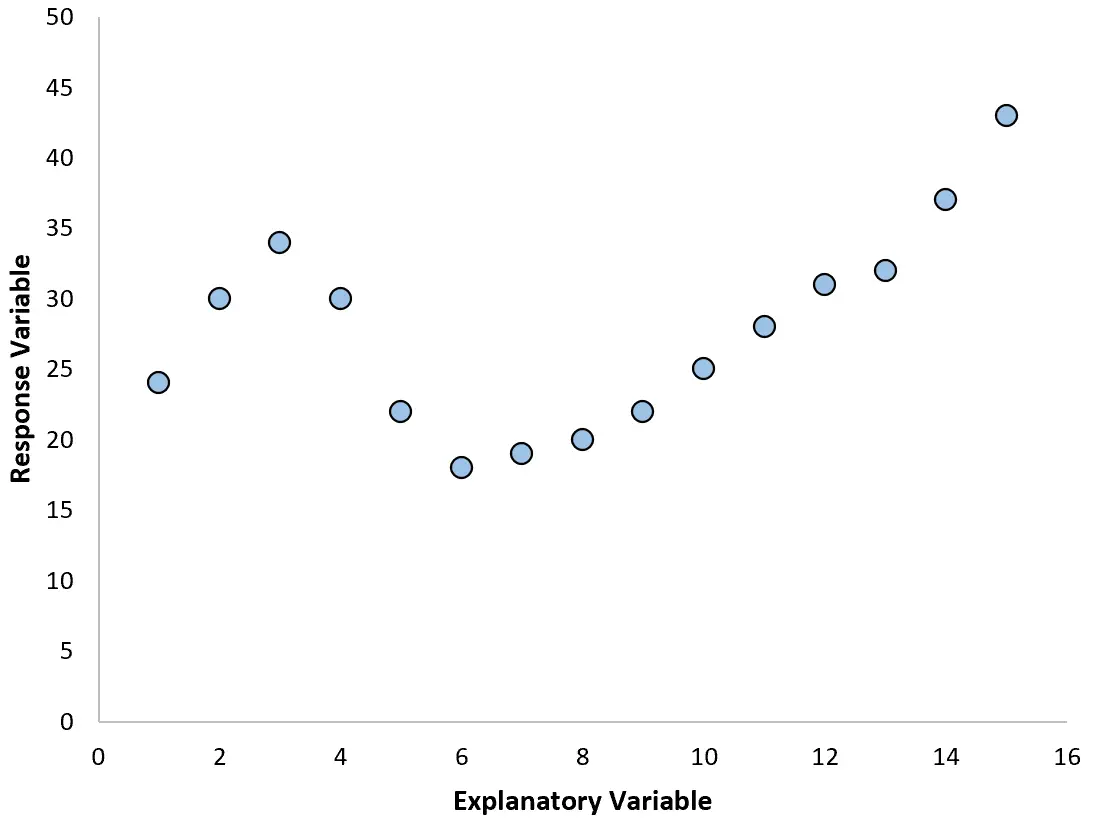
In deze gevallen is het zinvol om polynomiale regressie te gebruiken, die de niet-lineaire relatie tussen variabelen kan verklaren.

Deze zelfstudie biedt een stapsgewijs voorbeeld van hoe u polynomiale regressie kunt uitvoeren in Google Spreadsheets.

Stap 1: Creëer de gegevens

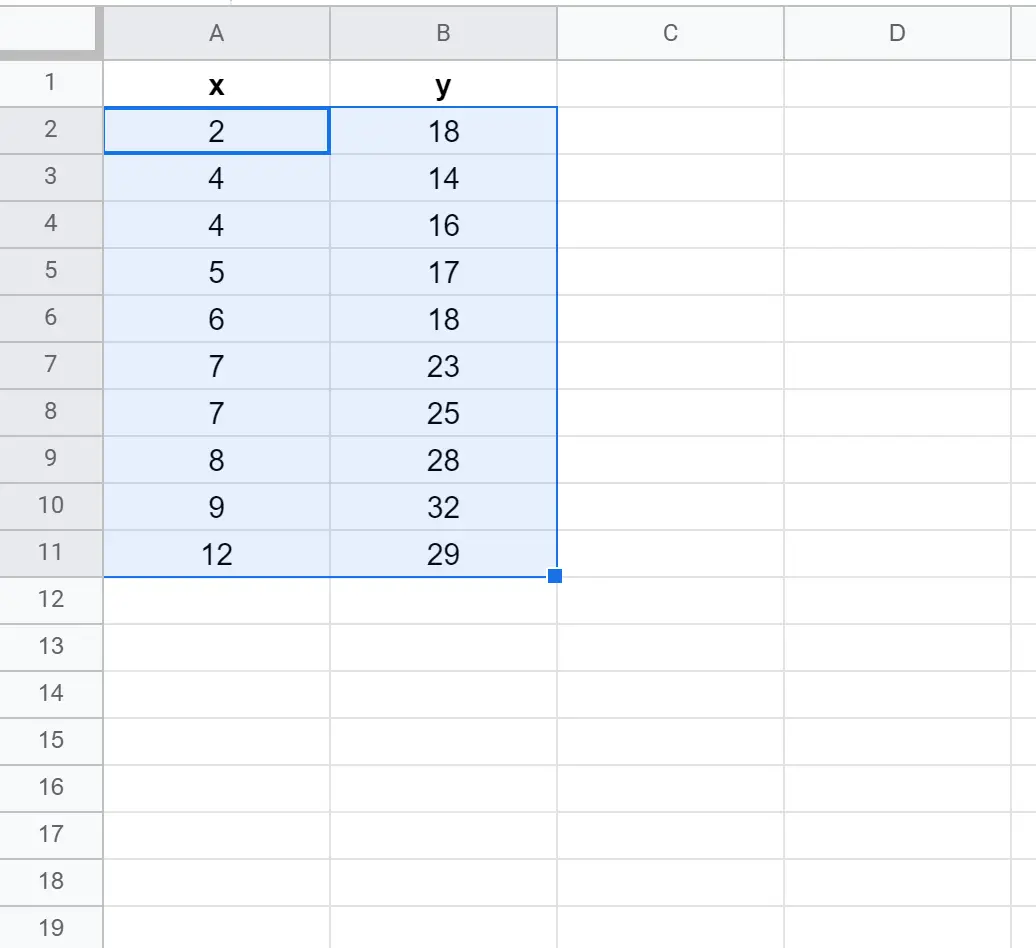
Laten we eerst een nep-dataset maken met de volgende waarden:

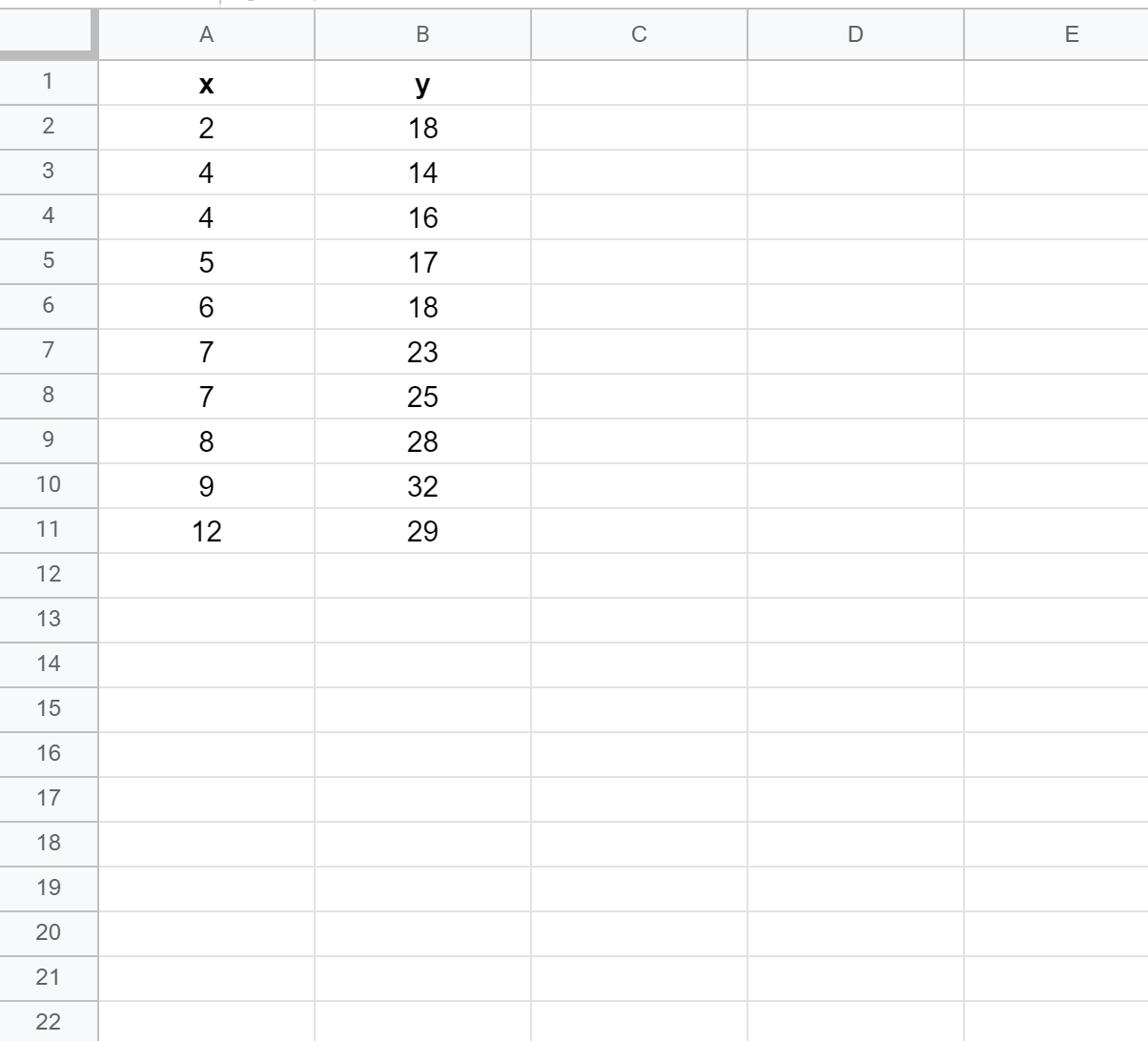
Stap 2: Maak een spreidingsdiagram

Vervolgens maken we een spreidingsdiagram om de gegevens te visualiseren.

Markeer eerst de cellen A2:B11 als volgt:

Klik vervolgens op het tabblad Invoegen en klik vervolgens op Grafiek in het vervolgkeuzemenu:

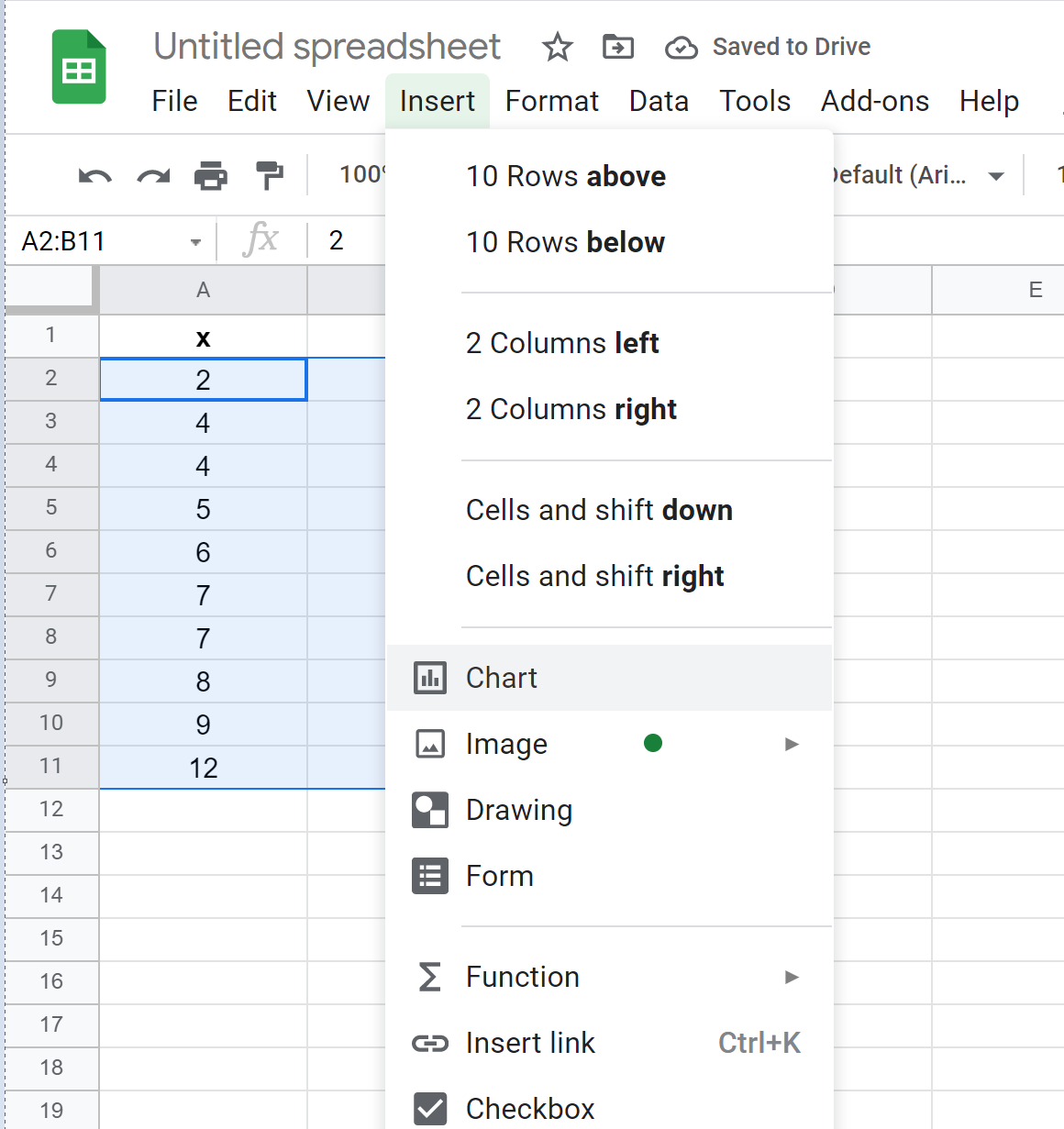
Standaard voegt Google Spreadsheets een spreidingsdiagram in:

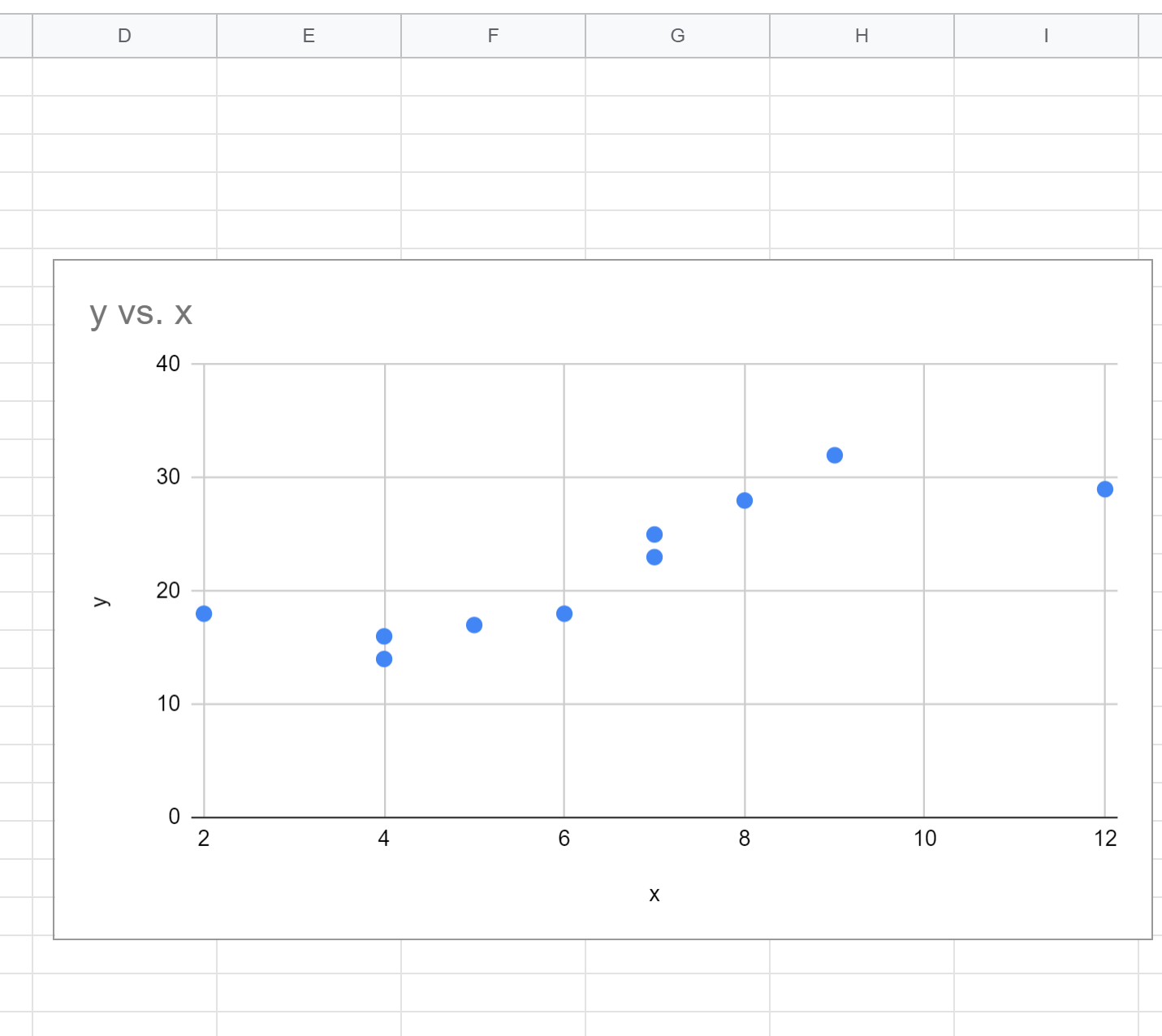
Stap 3: Zoek de polynomiale regressievergelijking

Dubbelklik vervolgens ergens op het spreidingsdiagram om het grafiekeditorvenster aan de rechterkant weer te geven:

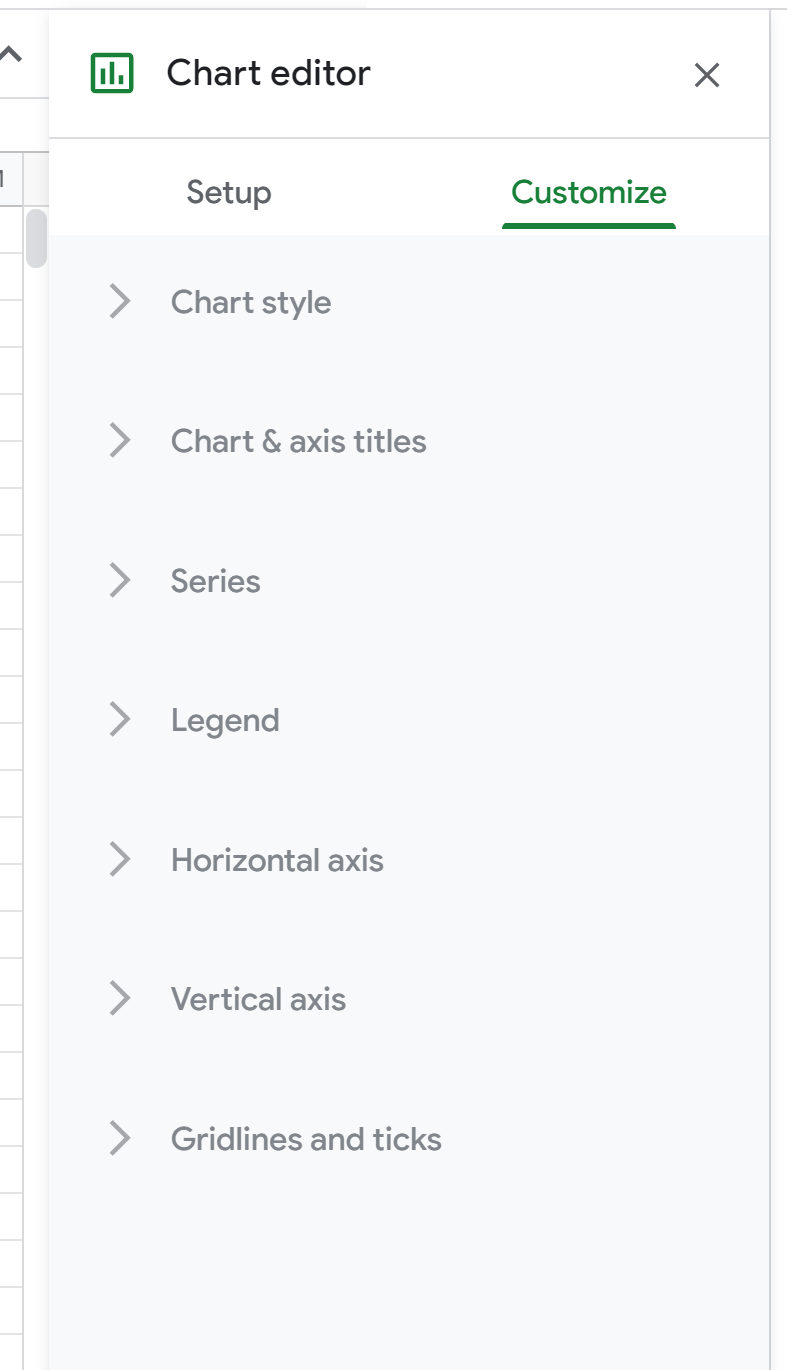
Klik vervolgens op Serie . Blader vervolgens naar beneden en vink het vakje naast Trendlijn aan en wijzig het Type in Polynomial . Kies bij Label de optie Gebruik vergelijking en vink vervolgens het selectievakje naast Show ^R2 aan.

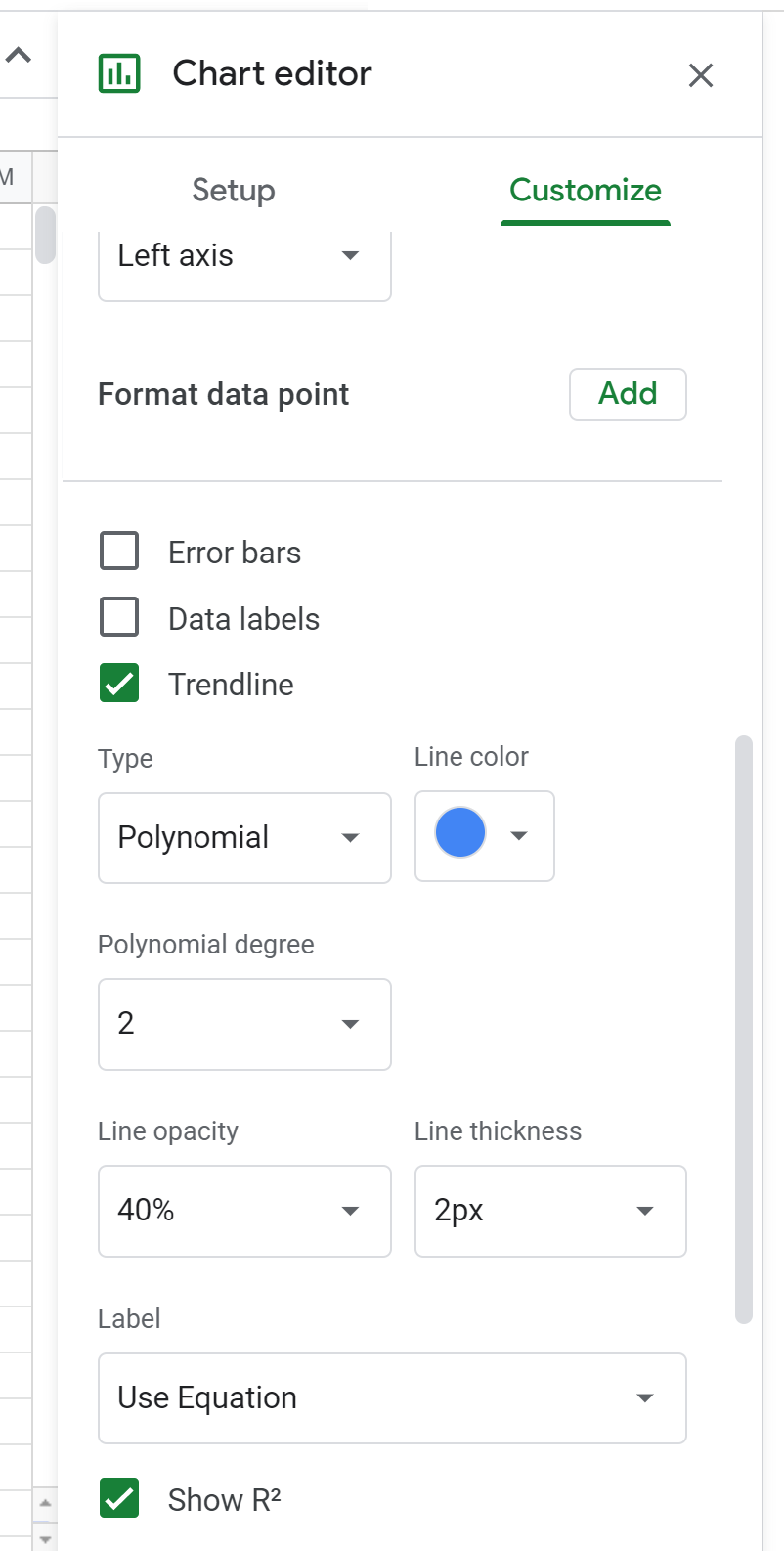
Hierdoor verschijnt de volgende formule boven het spreidingsdiagram:

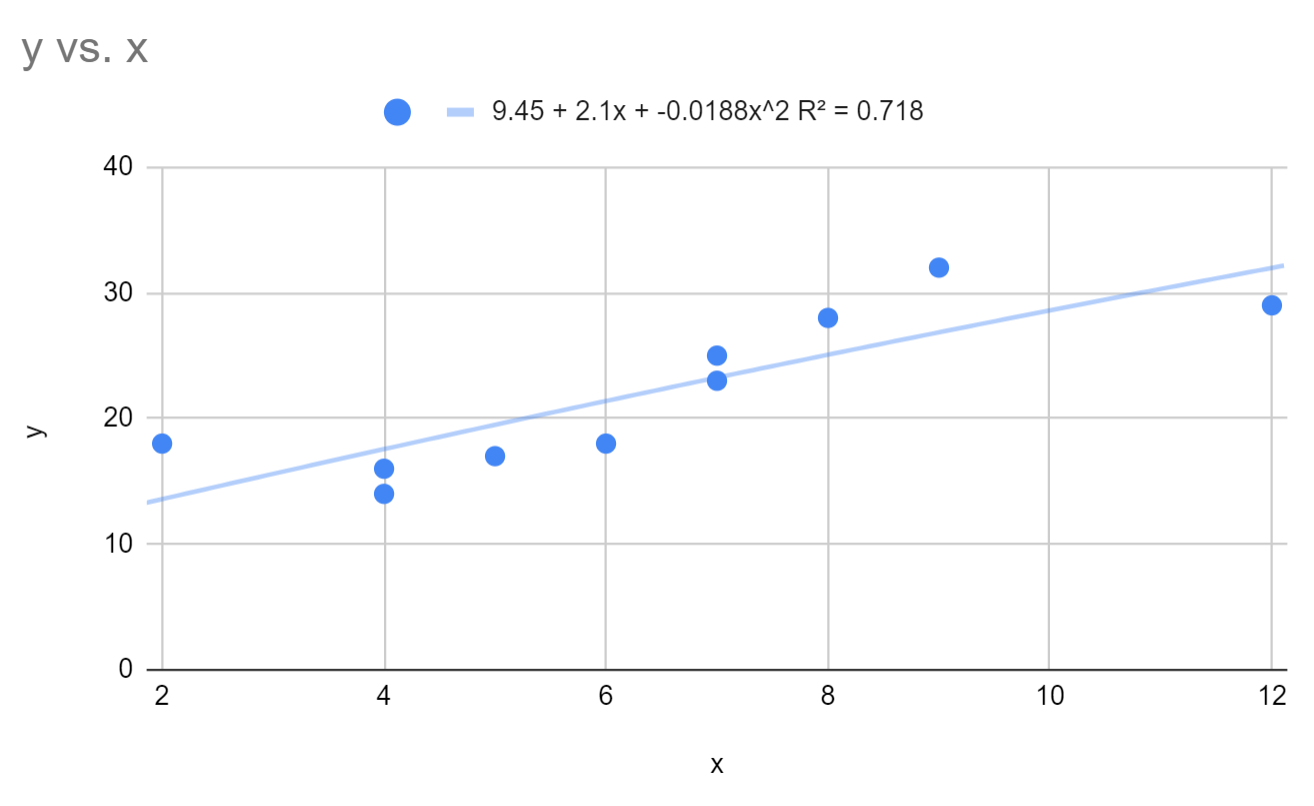
We kunnen zien dat de gepaste polynomiale regressievergelijking is:

y = 9,45 + 2,1x – 0,0188x ²

Het R-kwadraat voor dit model is 0,718 .

Bedenk dat R kwadraat ons het percentage variatie in de responsvariabele vertelt dat kan worden verklaard door de voorspellende variabelen. Hoe hoger de waarde, hoe beter het model.

Wijzig vervolgens de graad van de polynoom in 3 in de grafiekeditor:

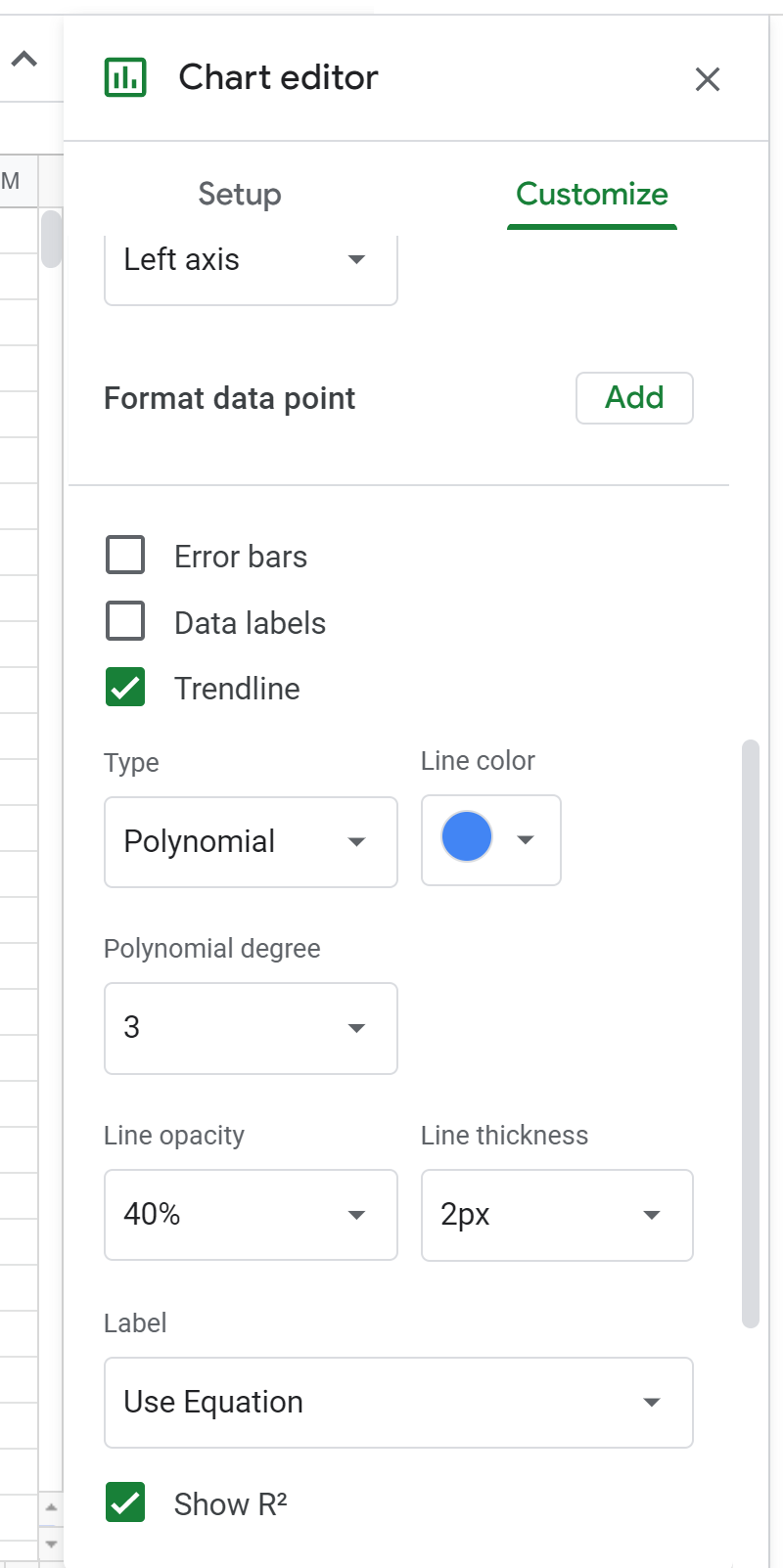
Hierdoor verschijnt de volgende formule boven het spreidingsdiagram:

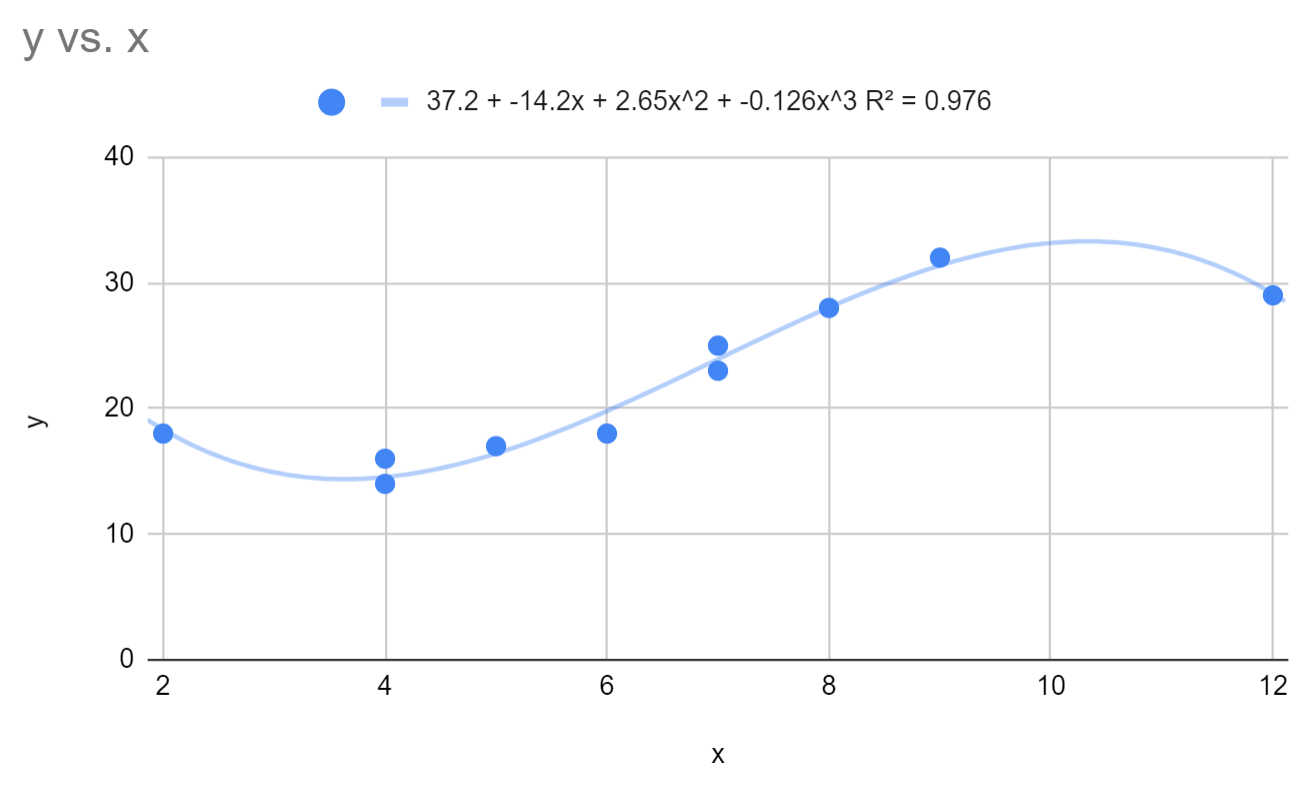
Dit verandert de aangepaste polynomiale regressievergelijking in:

y = 37,2 – 14,2x + 2,64x ² – 0,126x ³

Het R-kwadraat voor dit model is 0,976 .

Merk op dat de R-kwadraat van dit model aanzienlijk hoger is dan die van het polynomiale regressiemodel met een graad van 2. Dit suggereert dat dit regressiemodel aanzienlijk beter is in het weergeven van de trend van de onderliggende gegevens.

Als je de graad van de polynoom verandert in 4, neemt het R-kwadraat nauwelijks toe tot 0,981 . Dit suggereert dat een polynomiaal regressiemodel van graad 3 voldoende is om de trend in deze gegevens vast te leggen.

We kunnen de aangepaste regressievergelijking gebruiken om de verwachte waarde van de responsvariabele te vinden, gegeven een gegeven waarde van de voorspellende variabele. Als x = 4 bijvoorbeeld, zou de verwachte waarde voor y zijn:

y = 37,2 – 14,2(4) + 2,64(4) ² – 0,126(4) ³ = 14,576

Op deze pagina vindt u andere Google Spreadsheets-tutorials.