Hoe polynomiale regressie uit te voeren in sas

Het meest voorkomende type regressieanalyse iseenvoudige lineaire regressie , die wordt gebruikt wanneer een voorspellende variabele en eenresponsvariabele een lineair verband hebben.

Soms is de relatie tussen een voorspellende variabele en een responsvariabele echter niet-lineair.

In deze gevallen is het zinvol om polynomiale regressie te gebruiken, die de niet-lineaire relatie tussen variabelen kan verklaren.

In het volgende voorbeeld ziet u hoe u polynomiale regressie uitvoert in SAS.

Voorbeeld: polynomiale regressie in SAS

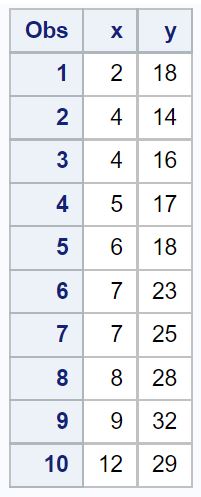
Laten we aannemen dat we de volgende gegevensset in SAS hebben:

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
2 18
4 14
4 16
5 17
6 18
7 23
7 25
8 28
9 32
12 29
;
run ;

/*view dataset*/
proc print data =my_data;

Stel nu dat we een spreidingsdiagram maken om de relatie tussen variabelen x en y in de gegevensset te visualiseren:

 /*create scatter plot of x vs. y*/
proc sgplot data =my_data;
    scatter x =x y =y;
run ; 

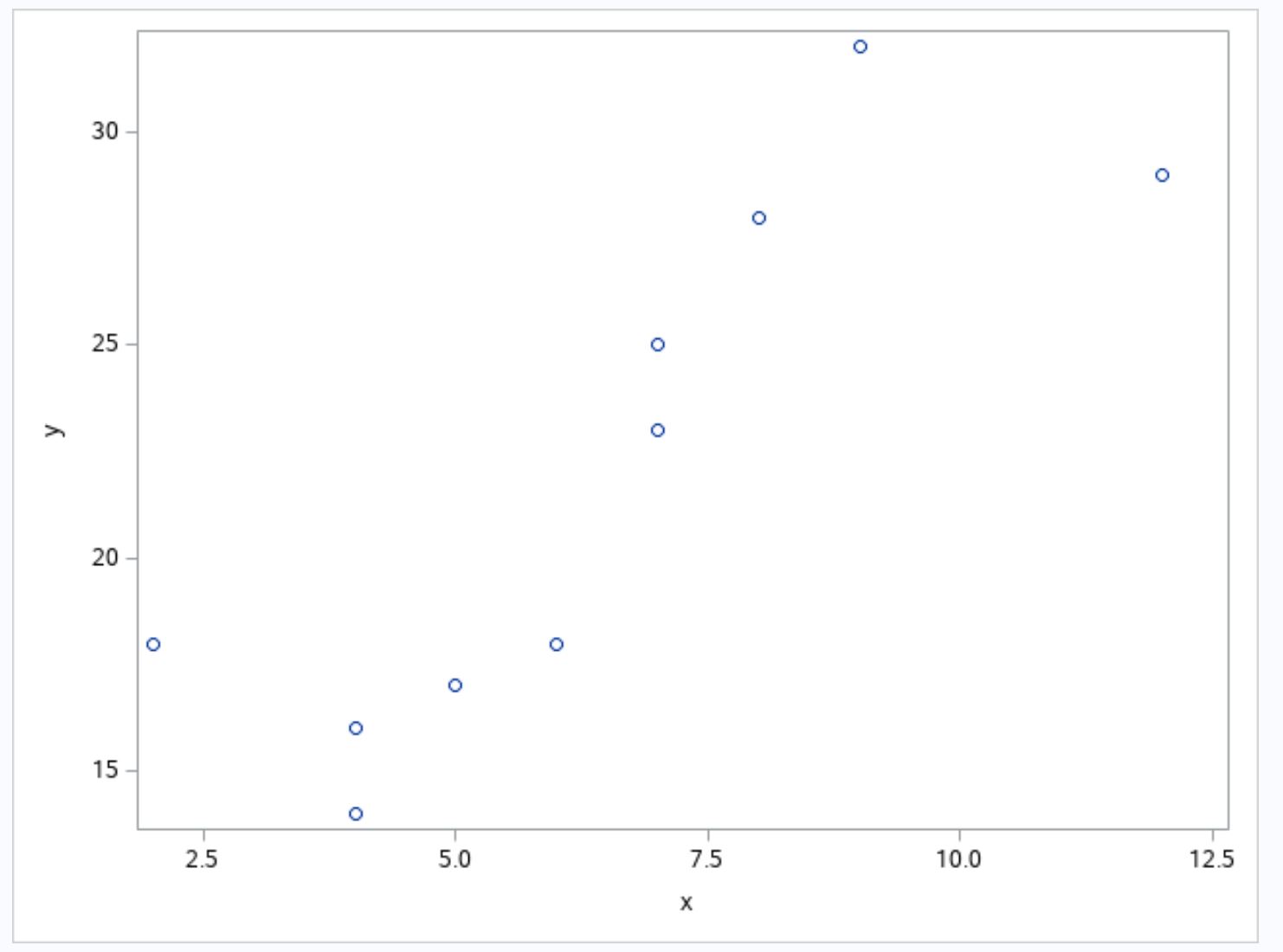
Uit de grafiek kunnen we zien dat de relatie tussen x en y kubisch lijkt.

We kunnen dus twee nieuwe voorspellende variabelen in onze dataset definiëren (x ² en x ³ ), en vervolgens proc reg gebruiken om een polynoom regressiemodel te passen met behulp van deze voorspellende variabelen:

 /*create dataset with new predictor variables*/
data my_data;
    input xy;
    x2 = x** 2 ;
    x3 = x** 3 ;
    datalines ;
2 18
4 14
4 16
5 17
6 18
7 23
7 25
8 28
9 32
12 29
;
run ;

/*fit polynomial regression model*/
proc reg data =my_data;
    model y = x x2 x3;
run ;

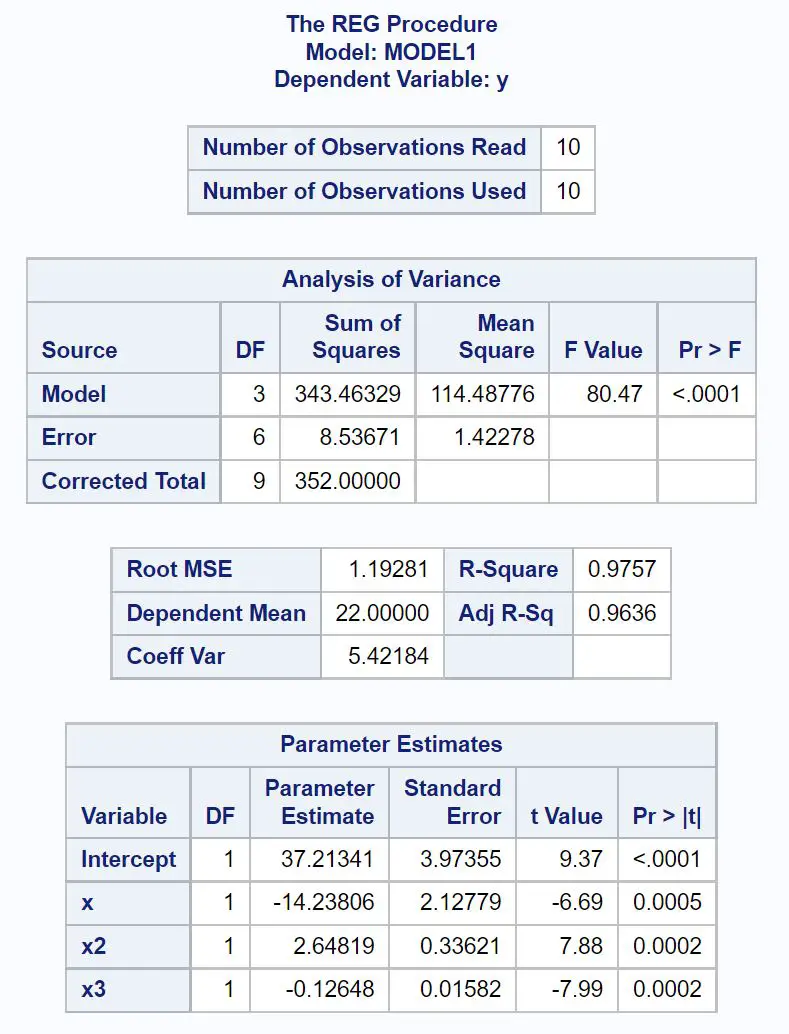
In de tabel Parameterschattingen kunnen we de schattingen van de coëfficiënten vinden en onze passende polynomiale regressievergelijking schrijven als:

y = 37,213 – 14,238x + 2,648x ² – 0,126x ³

Deze vergelijking kan worden gebruikt om de verwachte waarde van de responsvariabele te vinden, gegeven een gegeven waarde van de voorspellende variabele.

Als xa bijvoorbeeld de waarde 4 heeft, dan moet y de waarde 14,565 hebben:

y = 37,213 – 14,238(4) + 2,648(4) ² – 0,126(4) ³ = 14,565

We kunnen ook zien dat het polynomiale regressiemodel een aangepaste R-kwadraatwaarde van 0,9636 heeft, wat extreem dicht bij één ligt en ons vertelt dat het model uitstekend werk levert bij het aanpassen van de dataset.

Gerelateerd: Hoe aangepaste R-kwadraat te interpreteren (met voorbeelden)

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe kwantielregressie uit te voeren in SAS