Polynomiale regressie in r (stap voor stap)

Polynomiale regressie is een techniek die we kunnen gebruiken wanneer de relatie tussen een voorspellende variabele en een responsvariabele niet-lineair is.

Dit type regressie heeft de vorm:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

waarbij h de “graad” van de polynoom is.

Deze tutorial biedt een stapsgewijs voorbeeld van hoe u polynomiale regressie in R kunt uitvoeren.

Stap 1: Creëer de gegevens

Voor dit voorbeeld maken we een dataset aan met daarin het aantal gestudeerde uren en het eindexamencijfer voor een klas van 50 studenten:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Stap 2: Visualiseer de gegevens

Voordat we een regressiemodel op de gegevens toepassen, maken we eerst een spreidingsdiagram om de relatie tussen het aantal bestudeerde uren en de examenscore te visualiseren:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

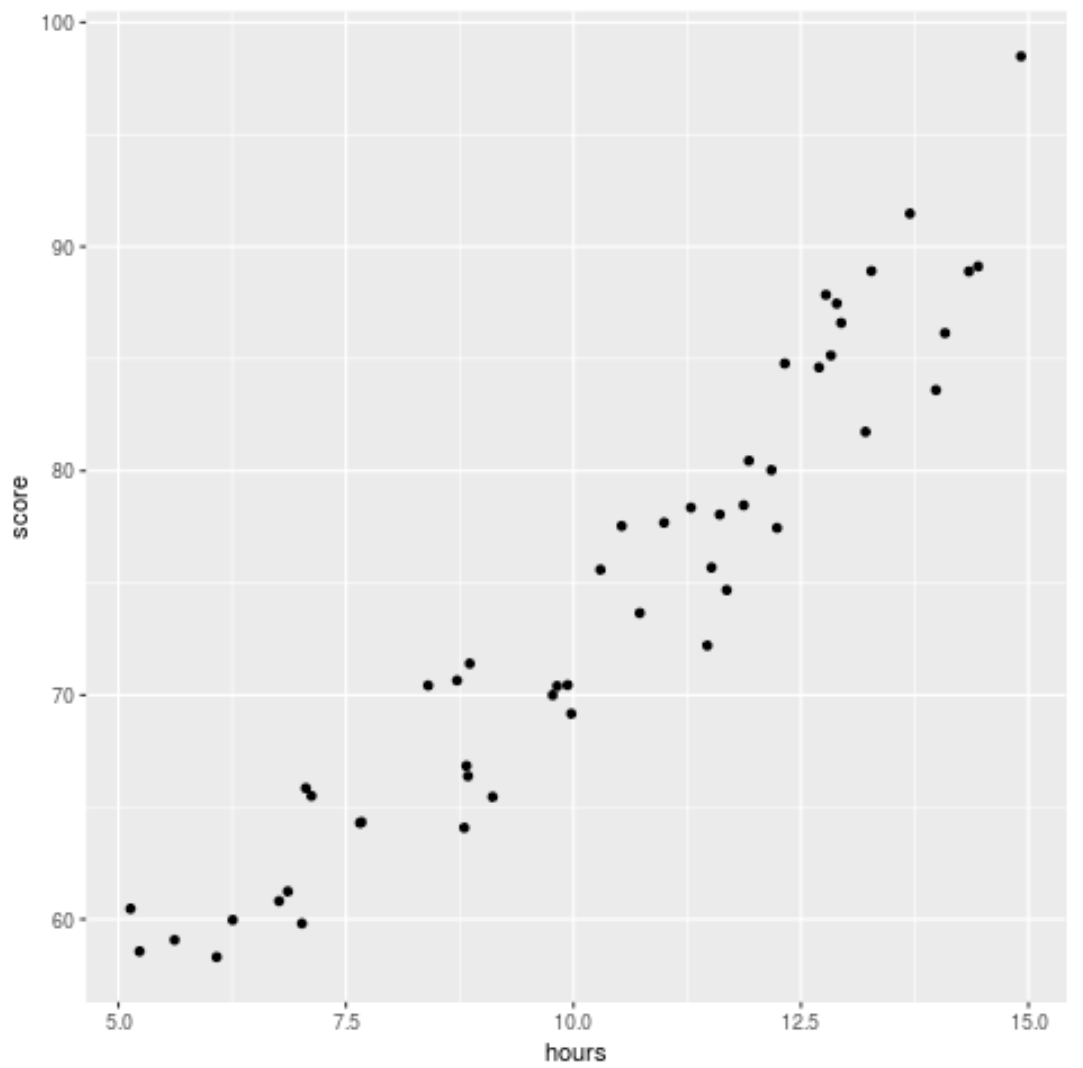
We kunnen zien dat de gegevens een enigszins kwadratisch verband hebben, wat aangeeft dat polynomiale regressie wellicht beter bij de gegevens past dan eenvoudige lineaire regressie.

Stap 3: Pas polynomiale regressiemodellen aan

Vervolgens passen we vijf verschillende polynomiale regressiemodellen aan met graden h = 1…5 en gebruiken we k-voudige kruisvalidatie met k = 10 keer om de MSE-test voor elk model te berekenen:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

Uit het resultaat kunnen we de MSE-test voor elk model zien:

• MSE-toets met graad h = 1: 9,80
• MSE-toets met graad h = 2: 8,75
• MSE-toets met graad h = 3: 9,60
• MSE-toets met graad h = 4: 10,59
• MSE-toets met graad h = 5: 13,55

Het model met de laagste test-MSE bleek het polynomiale regressiemodel met graad h = 2 te zijn.

Dit komt overeen met onze intuïtie uit het oorspronkelijke spreidingsdiagram: een kwadratisch regressiemodel past het beste bij de gegevens.

Stap 4: Analyseer het definitieve model

Ten slotte kunnen we de coëfficiënten van het best presterende model verkrijgen:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Uit het resultaat kunnen we zien dat het uiteindelijk gemonteerde model:

Score = 54,00526 – 0,07904*(uren) + 0,18596*(uren) ²

Met deze vergelijking kunnen we een schatting maken van de score die een student krijgt op basis van het aantal gestudeerde uren.

Een student die bijvoorbeeld 10 uur studeert, zou een cijfer van 71,81 moeten krijgen:

Score = 54,00526 – 0,07904*(10) + 0,18596*(10) ² = 71,81

We kunnen ook het aangepaste model plotten om te zien hoe goed het past bij de onbewerkte gegevens:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

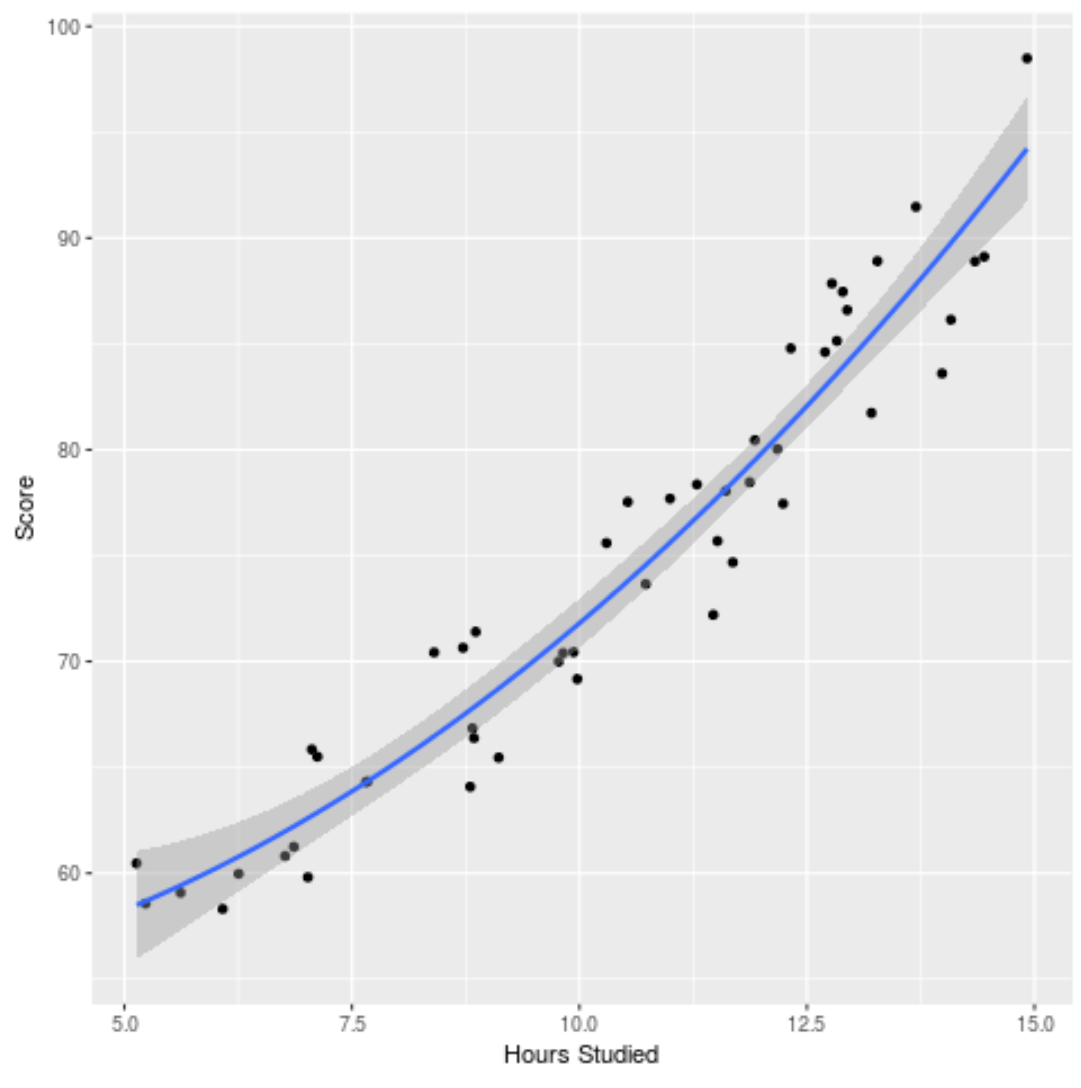
De volledige R-code die in dit voorbeeld wordt gebruikt, vindt u hier .