Polynomiale regressie uitvoeren met scikit-learn

Polynomiale regressie is een techniek die we kunnen gebruiken wanneer de relatie tussen een voorspellende variabele en een responsvariabele niet-lineair is.

Dit type regressie heeft de vorm:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

waarbij h de “graad” van de polynoom is.

Het volgende stapsgewijze voorbeeld laat zien hoe u polynomiale regressie in Python kunt uitvoeren met behulp van sklearn.

Stap 1: Creëer de gegevens

Laten we eerst twee NumPy-arrays maken om de waarden van een voorspeller en een responsvariabele vast te houden:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

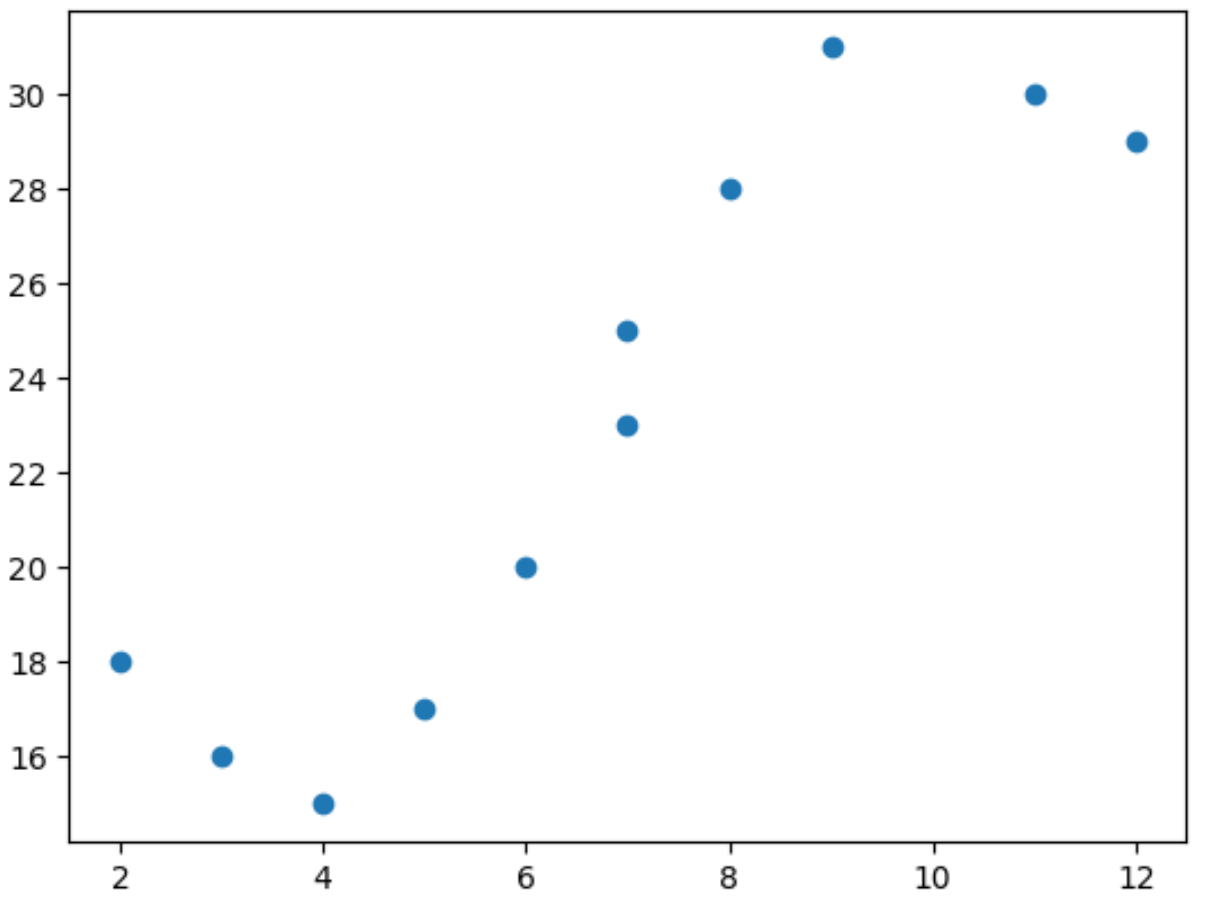
Uit het spreidingsdiagram kunnen we zien dat de relatie tussen x en y niet lineair is.

Het is daarom een goed idee om een polynomiaal regressiemodel aan de gegevens toe te passen om de niet-lineaire relatie tussen de twee variabelen vast te leggen.

Stap 2: Pas het polynomiale regressiemodel aan

De volgende code laat zien hoe u sklearn-functies kunt gebruiken om een polynoomregressiemodel van graad 3 in deze gegevensset te passen:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Met behulp van de modelcoëfficiënten die in de laatste rij worden weergegeven, kunnen we de aangepaste polynomiale regressievergelijking als volgt schrijven:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Deze vergelijking kan worden gebruikt om de verwachte waarde van de responsvariabele te vinden, gegeven een gegeven waarde van de voorspelde variabele.

Als x bijvoorbeeld 4 is, zou de verwachte waarde voor de responsvariabele y 15,39 zijn:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Opmerking : Om een polynoomregressiemodel met een andere graad te passen, wijzigt u eenvoudigweg de waarde van het graadargument in de functie PolynomialFeatures() .

Stap 3: Visualiseer het polynomiale regressiemodel

Ten slotte kunnen we een eenvoudige plot maken om het polynomiale regressiemodel te visualiseren dat is aangepast aan de oorspronkelijke gegevenspunten:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

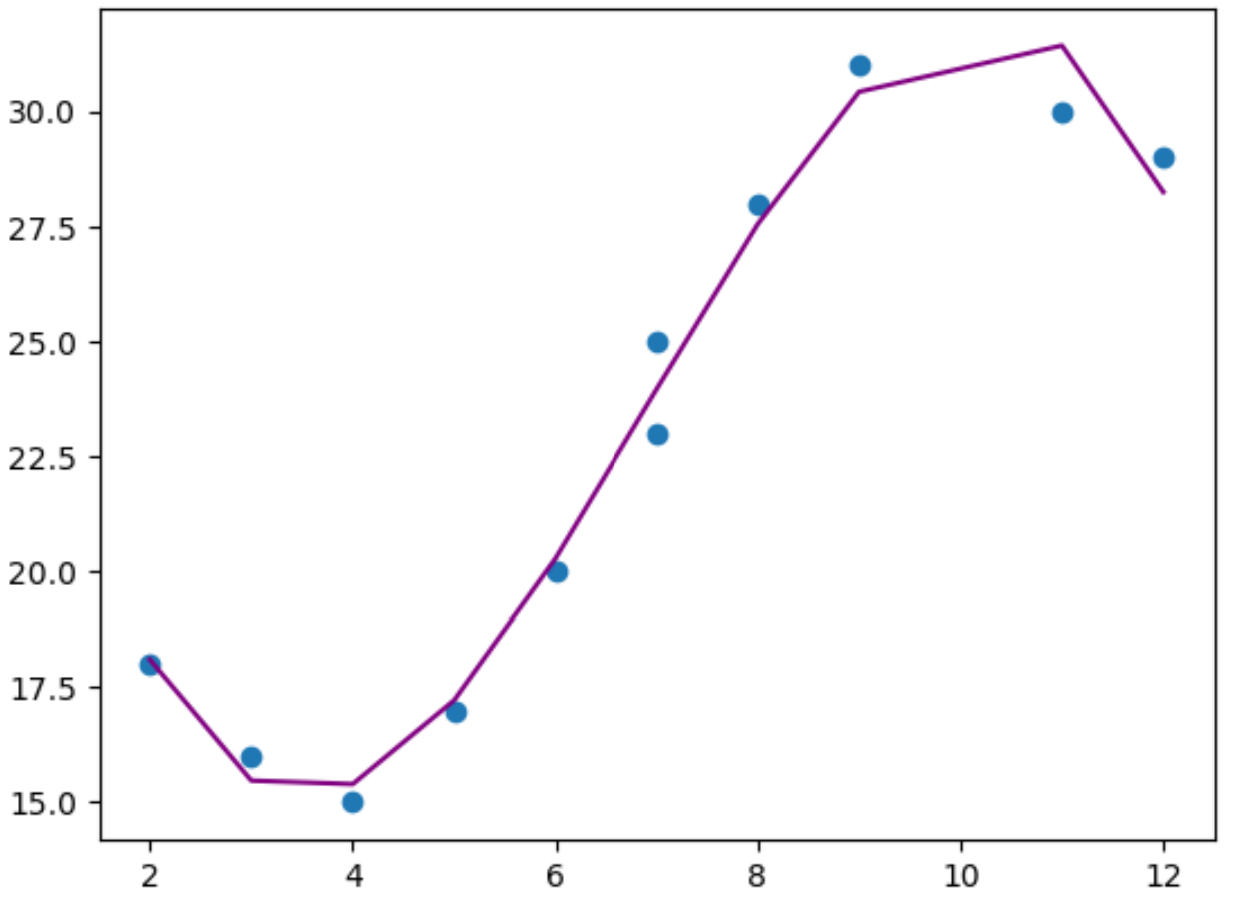
Uit de grafiek kunnen we zien dat het polynomiale regressiemodel goed bij de gegevens lijkt te passen zonder te overfitting .

Opmerking : u kunt de volledige documentatie voor de functie sklearn PolynomialFeatures() hier vinden.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken kunt uitvoeren met behulp van sklearn:

Hoe regressiecoëfficiënten uit sklearn te extraheren
Hoe u de gebalanceerde precisie kunt berekenen met behulp van sklearn
Hoe het classificatierapport in Sklearn te interpreteren